Задачи на движение: графический подход

Изобразим условие задачи в координатах по времени и положению в пространстве. Пусть точки и соответствуют выходам Ани и Бори из деревни А и деревни Б соответственно. Их скорости постоянны и одинаковы. Пусть Аня пришла в деревню Б в точке а Боря в деревню A — в точке Тогда они встретились в точке Если бы Аня вышла на полчаса раньше, она бы начинала путь в точке и пришла бы в Б в точке Аналогично для Бори и точек и Обозначим возможные точки встреч за и Проведем и параллельно оси а также и параллельно оси Треугольники и будут прямоугольными.

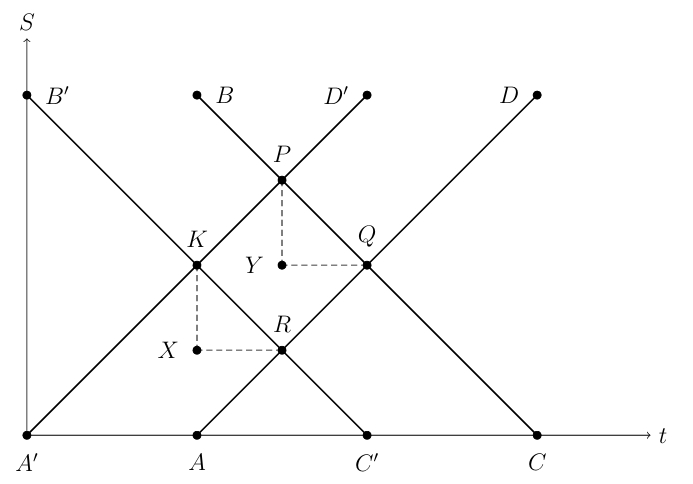
Заметим, что если бы Аня и Боря вместе вышли на 30 минут раньше, то их встреча произошла бы в том же месте, что и в действительности, поэтому точки и лежат на одной горизонтали. Если бы Аня вышла на 30 минут раньше, то встреча бы состоялась в точке что ближе к деревне Б на 2 километра, чем точка встречи Тогда Так как скорости Ани и Бори всегда одинаковые, и следовательно, — параллелограмм. Выходит, что отрезки и равны и параллельны. Тогда их проекции на ось будут равны. Выходит, что и Треугольники и равны, Если бы Боря вышел на 30 минут раньше, то встретились бы они в точке на 2 километра ближе к деревне А.