Увидеть расстояние между точками
Ошибка.
Попробуйте повторить позже
Найдите наименьшее значение выражения
Подсказка 1
Сумма корней с суммой двух квадратов внутри —> явный намёк на расстояние между точками и использование координатной плоскости! Постройте расстояния, зафиксировав где-то произвольно точку (x, y). А после начинайте её двигать – где достигается минимум? Попробуйте для этого что-то понять про неподвижные концы отрезков
Подсказка 2
Эти концы лежат на одной прямой! Чтобы минимизировать расстояние до двух концов, что лежат на осях Ox и Oy, двигающая вершина (x,y) должна лежать на…? А тогда мы в точности можем сделать расстояние до оставшейся вершины самым минимальным, что только возможно (какое минимальное расстояние между точками?) – вот мы строго оценили и тут же построили конструкцию-пример!
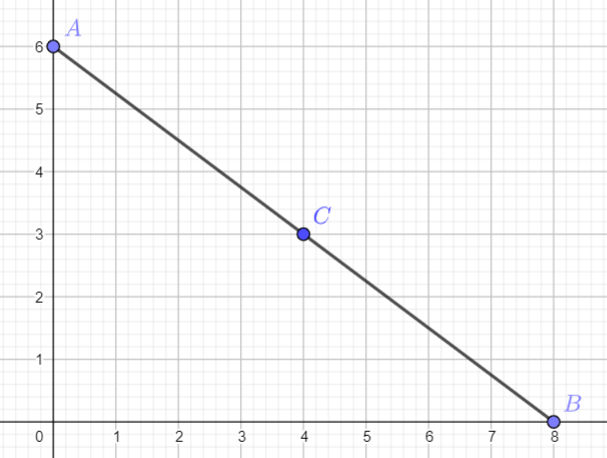
Отметим точки с координатами . Заметим, что эти три точки лежат на одной прямой, а выражение из условия
является суммой длин отрезков
, где
имеет координаты
. По неравенству треугольника
. С
учётом очевидного неравенства
, тогда получаем
, причём оценка является точной, потому что равенство
достигается при
.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




