Тема Геометрия помогает алгебре

Увидеть расстояние между точками

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела геометрия помогает алгебре

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#79605

Наименьшее значение функции

∘ -2---2 ∘ -2--2- ∘ -2--2- ∘ -2-------2 x1+ 1 + x2+ 2 + x3+ 3 +...+ x2024+2024

для неотрицательных $x1,x2,...,x2024$ , сумма которых равна $k$ , равно $2024⋅2025$ . При каком значении параметра $k$ такое возможно?

Источники: ОММО - 2024, задача 7 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Давайте внимательнее посмотрим на задачу и попробуем вспомнить хитрый способ решения неравенств, нахождения минимума или максимума. Напоминают ли вам что-то квадратные корни из суммы квадратов? Где вы такое могли видеть?

Подсказка 2

Давайте ещё подумаем, чтобы не сразу раскрывать вам все "секреты". Могли ли вы встречать подобное в геометрии? Может быть это длина какого-то отрезка?

Подсказка 3

Верно, это же теорема Пифагора, где числа под корнями являются катетами прямоугольного треугольника. Как же теперь можно проиллюстрировать нашу задачу?

Подсказка 4

Да, получается мы можем расположить отрезки с иксами вдоль одной прямой, а с числами вдоль перпендикулярной ей. В итоге, у нас получится ломанная. Понятно, что минимумом будет просто расстояние между крайними точками ломанной, а это гипотенуза с катетами из суммы наших катетов. Осталось понять, что мы знаем обе суммы и из условия про минимум найти k, решив уравнение. Победа!

Показать ответ и решение

На оси абсцисс отметим отрезки, равные по длине $x,x ,...,x 1 2 2024$ , а на оси ординат — отрезки длины $1,2,...,2024$ . Тогда выражение $∘ -2--- x1+1$ — это расстояние от точки $(0,0)$ до точки $(x1,1)$ , а $∘ 2---2- x2 +2$ — расстояние от точки $(x1,1)$ до точки $(x2+ x1,3)$ .

$PIC$

Таким образом, получили ломанную из точки $(0,0)$ до точки с координатами

$(x1+ ...+ x2024,2024⋅22025) =(k,2024⋅22025)$ . Ее длина не превосходит расстояния между этими точками, то есть

( ) ∘x2-+12+ ∘x2-+22+ ∘x2+-32+ ...+ ∘x2--+-20242 ≥ 2024⋅2025 2+k2 1 2 3 2024 2

Тогда

∘ (--------)2---- 2024⋅2025= 2024⋅2025 + k2 2

Решив это уравнение, находим

√3 k = 2-⋅2024 ⋅2025

Ответ:

$2025⋅1012√3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#99294

Найдите минимум выражения

∘ -2--- ∘ -2--- ∘ -2--- ∘ 2---- x +1 + y +4 + z +9 + t +16

при условии $x +y +z+ t= 10$ и $x,y,z,t$ — положительны.

Показать ответ и решение

Перепишем исходное выражение, как

∘ 2---2- ∘-2---2 ∘-2---2 ∘ -2--2 x +2 + y + 2 + z + 3 + t +4

Заметим, что каждое из четырёх слагаемых это расстояние между точками $OA,AC,D,DE.$

$PIC$

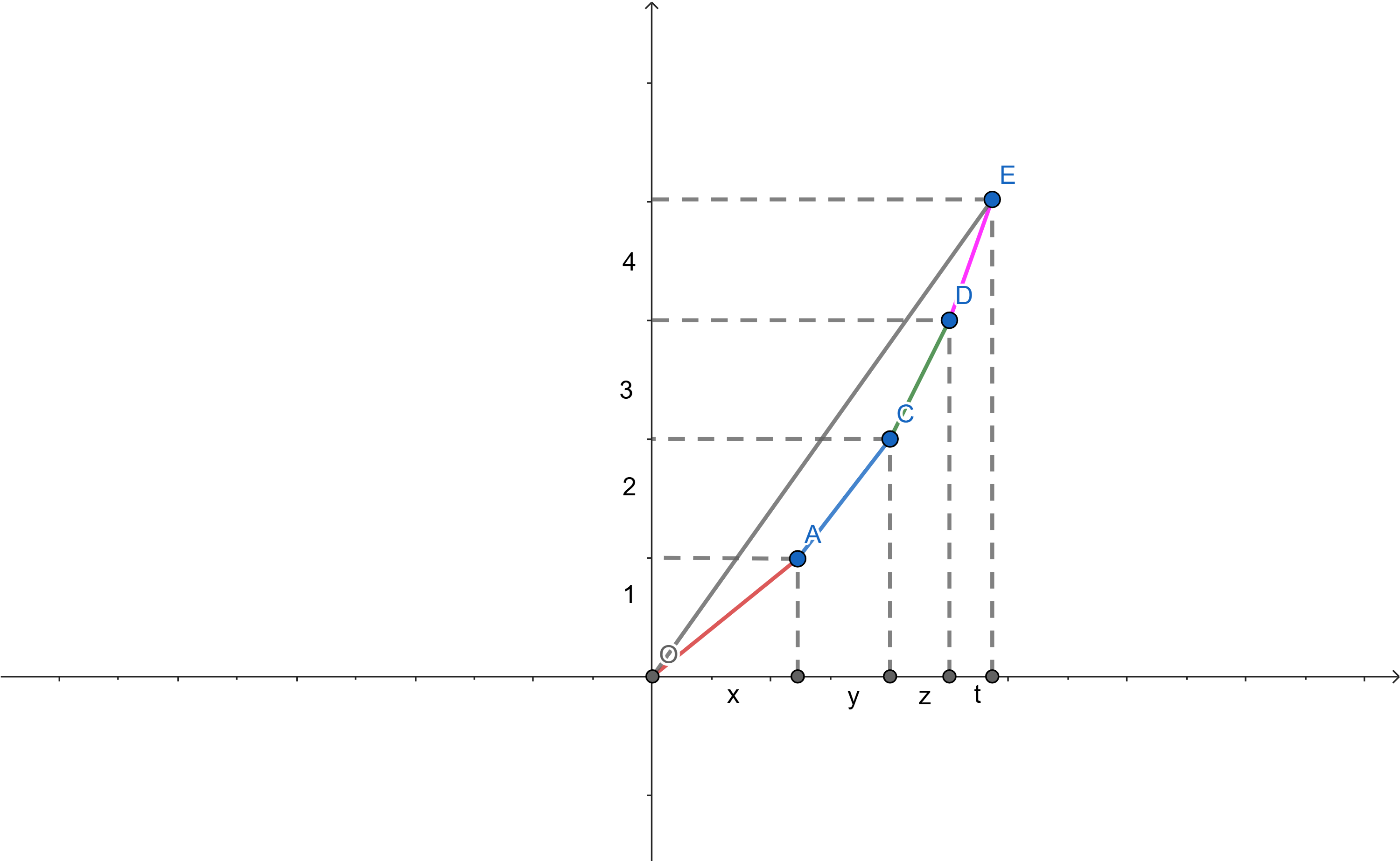
По неравенству ломанной это сумма минимальна, когда все отрезки лежат на $OE$ и тогда сумма их длин по теореме Пифагора равна $√- 10 2,$ причём равенство достигается при $x =1;y = 2;z = 3;t= 4.$

Ответ:

$10√2$

Ошибка.
Попробуйте повторить позже

Задача 3#99295

Найти наименьшее значение выражения

∘ -2--2- ∘ -----2------2- x + y + (5 − x) + (5− y).

Показать ответ и решение

Заметим, что первое слагаемое задаёт расстояние от точки $A(0;0)$ до точки $B(x;y),$ второе слагаемое задаёт расстояние от точки $B (x;y)$ до точки $C (5;5).$

$PIC$

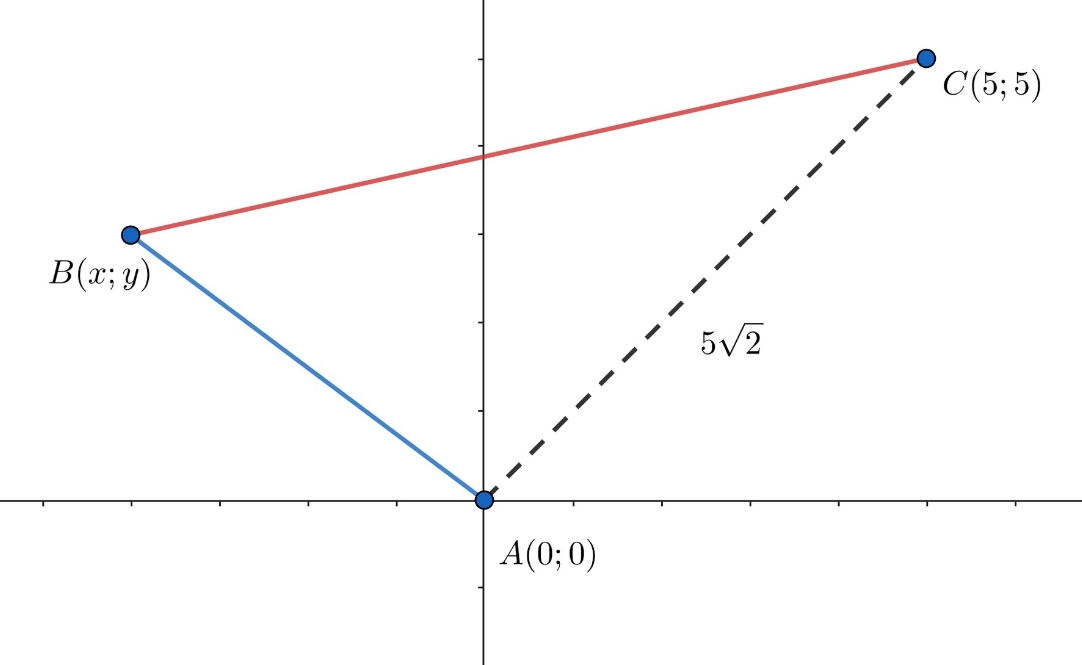
По неравенству треугольника для $△ABC$

∘ ------ ∘ -------------- √- x2 +y2+ (5− x)2 +(5− y)2 ≥ 5 2

Таким образом, минимальное значение достигается, когда точка $B$ лежит на отрезке $AC$ при $x =y =1 :$

√ - √ - √ - 2+4 2= 5 2

Ответ:

$5√2$

Ошибка.
Попробуйте повторить позже

Задача 4#69930

Найти решение уравнения в натуральных числах $x$ и $y :$

∘ 2---2------------ ∘-2---2------------ x +y − 2x− 6y +10+ x + y − 18x − 6y+ 90− 10 =0

Источники: САММАТ-2023, 11.7 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

У нас в задаче присутствует равенство √a+√b=c. Хочется возвести в квадрат, но, если возводить прямо так, у нас получится произведение корней √ab. Поэтому разумно было бы перенести один корень направо и возвести в квадрат...

Подсказка 2

После возведения в квадрат и приведения подобных, можно оставить корень в одной стороне, а все остальное отправить в другую и опять возвести в квадрат. Можно ли как-то после этого удачно сгруппировать слагаемые?

Подсказка 3

Получается следующее: (x-5)²/5²+(y-3)²/3²=1. Но тогда |x-5|≤5 и |y-3|≤3 ⇔ 0≤x≤10 и 0≤y≤6. Осталось перебрать x и y и найти искомые решения!

Показать ответ и решение

Если выделить полные квадраты под корнями, то уравнение можно записать в виде

∘-------------- ∘-------------- (x− 1)2+ (y− 3)2+ (x− 9)2+ (y− 3)2 = 10

Этому уравнению удовлетворяют такие пары точек $(x,y)$ , сумма расстояний от которых до точек $(1,3)$ и $(9,3)$ равна $10.$

Множеством точек плоскости, обладающих таким свойством, является эллипс. По его фокусам легко восстановить канонический вид уравнения (центр эллипса находится в середине между фокусами, координаты считаются как полусумма, соответственно считаются и длины больших полуосей):

(x− 5)2 (y− 3)2 --52--+ --32-- =1

Перебором $5≤ x≤ 10$ и $3≤y ≤6$ можно найти решения $(5,6)$ и $(10,3)$ , а им из симметрии соответствуют пары $(5,0)$ и $(0,3)$ . В ответ же записываем только пары, у которых обе компоненты натуральные.

Ответ:

$(10,3),(5,6)$

Ошибка.
Попробуйте повторить позже

Задача 5#34720

Положительные вещественные числа $x$ , $y$ , $z$ удовлетворяют условию $x +y+ z = 8$ . Докажите, что

∘ -2--- ∘ -2--- ∘ -2--- x + 1+ y + 4+ z + 9≥ 10.

Подсказки к задаче

Подсказка 1

Сумма корней с суммой двух квадратов внутри —> явный намёк на расстояние между точками и использование координатной плоскости! Интерпретируйте эту сумму как сумму длин звеньев ломаной! Где тогда находится отрезок, равный x+y+z?

Подсказка 2

Нужно доказать неравенство –> вспоминаем, какое самое распространённое геометрическое неравенство мы знаем, и используем его, чтобы добить задачку!

Показать доказательство

$PIC$

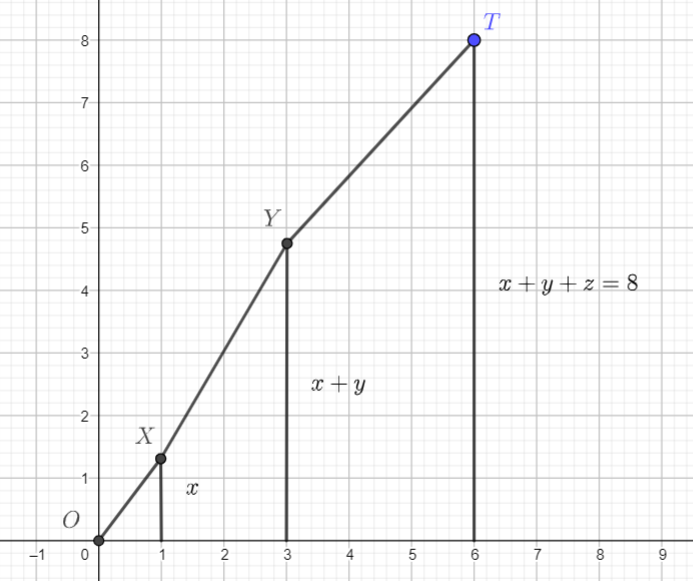
Построим отрезки перпендикулярно оси $Ox$ из точек с координатами $1,3$ и $6$ длинами $x,x+ y$ и $x+ y+ z$ (все числа по условию положительные) соответственно с концами в $X,Y$ и $T$ . Тогда сумма в левой части неравенства по формуле расстояния между точками равна $√------ OX + XY +Y T ≥ OT = 82+ 62 =10$ по неравенству ломаной, что и требовалось.

Ошибка.
Попробуйте повторить позже

Задача 6#34722

Найдите наименьшее значение выражения

∘-2-------2 ∘-----2-------2 ∘-----2---2 x + (y− 6) + (x− 4)+ (y− 3) + (x− 8)+ y .

Подсказки к задаче

Подсказка 1

Сумма корней с суммой двух квадратов внутри —> явный намёк на расстояние между точками и использование координатной плоскости! Постройте расстояния, зафиксировав где-то произвольно точку (x, y). А после начинайте её двигать – где достигается минимум? Попробуйте для этого что-то понять про неподвижные концы отрезков

Подсказка 2

Эти концы лежат на одной прямой! Чтобы минимизировать расстояние до двух концов, что лежат на осях Ox и Oy, двигающая вершина (x,y) должна лежать на…? А тогда мы в точности можем сделать расстояние до оставшейся вершины самым минимальным, что только возможно (какое минимальное расстояние между точками?) – вот мы строго оценили и тут же построили конструкцию-пример!

Показать ответ и решение

$PIC$

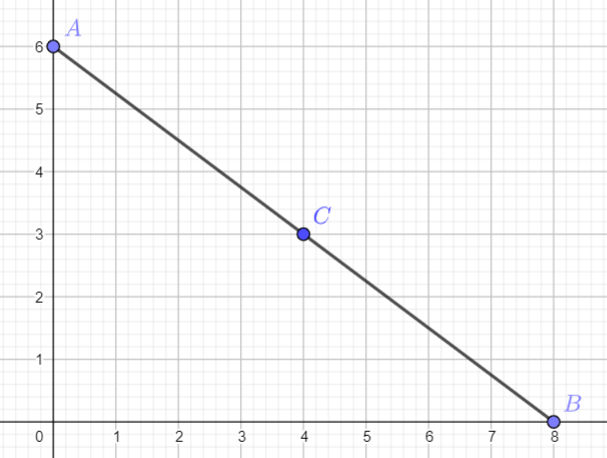
Отметим точки с координатами $A(0,6),C(4,3),B(8,0)$ . Заметим, что эти три точки лежат на одной прямой, а выражение из условия является суммой длин отрезков $AX + CX + BX$ , где $X$ имеет координаты $(x,y)$ . По неравенству треугольника $AX + BX ≥AB = 10$ . С учётом очевидного неравенства $CX ≥ 0$ , тогда получаем $AX + BX +CX ≥ 10$ , причём оценка является точной, потому что равенство достигается при $X =C$ .

Ответ:

$10$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#36670

Решите систему уравнений

{ ∘x2-+y2+-12x-+36+ ∘x2-+y2−-16y-+64= 10, 5y2− 8x2 = 8.

Показать ответ и решение

Первое уравнение системы можно переписать в виде:

∘ -----2---2 ∘ -2-------2 (x+ 6) + y + x + (y− 8) = 10.

Отметим на координатной плоскости точки $A(−6,0),B(0,8),X (x,y)$ . Тогда уравнение задаёт соотношение на длины отрезков $AX + BX = AB$ . Вспомним, что в неравенстве треугольника ( $AX + BX ≥AB$ ) равенство может достигаться только в случае вырожденности треугольника. Итак, первое уравнение эквивалентно условию, что точка $X$ лежит на отрезке $AB$ , то есть лежит на прямой $4 y = 3x+ 8$ при дополнительных условиях $− 6 ≤x ≤0 ≤y ≤ 8$ . Подставим во второе уравнение системы:

( 16 64 ) 5⋅ 9-x2 +-3 x +64 − 8x2 = 8 ⇐⇒ x2 +120x+ 351= 0 ⇐⇒ x= −60± 57

Корень $x = −117$ не подходит под условие $− 6≤ x$ , так что не входит в решения системы.

Корень $x = −3$ подходит под условие $− 6≤ x≤ 0$ .

Соответствующее значение $y = 43x +8 =4$ подходит под ограничения $0≤ y ≤ 8.$

Ответ:

$(−3;4)$

Ошибка.
Попробуйте повторить позже

Задача 8#91962

Решите систему уравнений

{ 3x +4y = 26; ∘ (x−-10)2+-(y−-5)2+∘ (x− 2)2+-(y+-1)2 = 10.

Показать ответ и решение

Рассмотрим второе уравнение. Если $A(0,0)$ , $B(x− 10,y− 5)$ и $C(− 8,− 6)$ , то второе уравнение превращается в $10= AB + BC ≥AC = 10$ . Значит, точки $A, B$ и $C$ лежат на одной прямой и $(x− 10) :(y− 5)=− 8:−6$ . Тогда $6(x − 10)= 8(y− 5)$ и $3x+ 4y = 26$ . Отсюда $3x= 4(y− 5)+30= 26− 4y$ , $y =2$ и $x =6$ . Проверяем, что эта точка подходит (это необходимо, так как пока мы знаем, что точка $B$ лежит на прямой $AC$ , а нам еще нужно, чтобы она лежала между точками $A$ и $C$ ).

Ответ: (6; 2)

Ошибка.
Попробуйте повторить позже

Задача 9#91966

Решите систему уравнений

{ 21+x = 32y√2; ∘x2-+-y2+2−-2x−-2y+∘x2-+-y2− 6x+-9= √5.

Показать ответ и решение

∘ -2---2---------- ∘ -2---2------ x + y +2− 2x− 2y+ x + y − 6x+ 9=

∘ -----2------2- ∘ -----2--2- √ - = (x − 1) + (y− 1) + (x − 3) + y = 5

Пусть $A(0,0)$ , $B (x − 1,y− 1)$ , $C(2,−1)$ . Тогда

√ - ∘ -----2-------2 ∘ -----2---2 √- 5= AC ≥AB + BC = (x− 1) + (y − 1) + (x− 3) + y = 5

Раз достигается равенство, то $B$ лежит на прямой $AC$ и $(x− 1):(y− 1)=2 :−1$ . Значит, $2y− 2 +x − 1= 0$ . Тогда $y = 3−x= 21+√x 2 32 5$ и $21+x x−3 32√5-+ -2-= 0$ . Заметим, что если посмотреть на это как на функцию от $x$ , то она возрастает и поэтому будет не более 1 корня. Это корень $x= 2.5$ , так как $1+x 232√5 = 2x−4.5$ и $1+x 232√5-+ x−23= 2− 2− 14 = 0$ .

Ответ:

$(2,5;0,25)$

Ошибка.
Попробуйте повторить позже

Задача 10#91967

Найдите все значения параметра $a$ , при каждом из которых система уравнений

{ x2 +(2a− 2)x+ a2− 2a− 3= 0 ∘x2-+-(y-− a)2+∘ (x+-4)2+-(y-− a)2 = 4

имеет ровно одно решение.

Показать ответ и решение

Перепишем первое уравнение.

2 (x− (a− 1)) = 4

Значит, $x= a− 1±2$ . Пусть $A(0,0)$ , $B(x,y− a)$ , $C(−4,0)$ . Тогда по условия $AB +BC = 4≥ AC =4$ . Значит, они лежат на одной прямой и поэтому $y− a= 0$ и $x∈ [− 4;0]$ .

Значит, $y = a$ и $x= a− 1− 2$ или $x= a− 1+ 2,$ если эти числа лежат в $[−4;0]$ . Первое значение $x$ попадает в интервал при $a ∈[−1;3]$ , а второе при $a∈[−5;−1]$ . Значит, ответ $[− 5;−1)∪ (− 1;3]$ .

Ответ:

$[−5;− 1)∪(−1;3]$

Ошибка.
Попробуйте повторить позже

Задача 11#92432

Даны положительные действительные числа $a,b,c$ . Известно, что

(a − b)lnc+ (b− c)ln a+(c− a)lnb= 0.

Докажите, что

(a − b)(b− c)(c− a)= 0.

Источники: Курчатов - 2021, 11.6 (см. olimpiadakurchatov.ru)

Подсказки к задаче

Подсказка 1

Если а = с, то задача решена. Поэтому рассмотрим случай, когда а ≠ с. Поделим каждую часть уравнения на a - c и перенесём ln(b) в другую сторону.

Подсказка 2

Обозначим k = (b-c)/(a-c), 1-k = (a-b)/(a-c) и перепишем условие, которое мы получили в прошлой подсказке. Введём систему координат и точки А, B, C, координаты которых будут удовлетворять функции y = ln(x).

Подсказка 3

Вспомните, как выглядит график y = ln(x). Может ли прямая пересекать этот график в трёх точках A, B, C, если ни одна из точек не совпадает с другой?

Показать доказательство

Если $a =c$ , то всё очевидно. Если $a⁄= c$ , поделим равенство на $a− c$ и перенесём $lnb$ в другую часть, получим

b−-c a−-b lnb= a− clna+ a− clnc.

Рассмотрим на координатной плоскости две точки: $A (a;lna)$ и $C(c;lnc)$ , а также обозначим $b−c α =a−c,$ тогда $a−b 1− α= a−c$ .

Точка $B$ с координатами $xB = αa+ (1− α )c= b$ и $yB = αlna+ (1− α)ln c= lnb$ лежит на прямой $AC$ .

Но также ясно, что эти три точки лежат на графике функции $y = lnx$ . Так как эта функция является вогнутой (например, потому, что её вторая производная отрицательна), то с прямой может пересекаться максимум по двум точкам, а это значит, что какие-то два из трёх чисел $a,b,c$ совпадают:

(a− b)(b− c)(c− a) =0

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#100192

Найдите все значения параметра $a$ , при каждом из которых неравенство

-----------1---------- √- √x2-+2x-+5+ √x2+-6x+-18-≤ a

выполняется при всех значениях $x.$

Показать ответ и решение

Так как знаменатель функции

-----------1---------- f(x)= √x2-+2x+-5+ √x2+-6x+18-

равен

∘ ---------- ∘ ---------- g(x)= (x +1)2+22+ (x +3)2+32

и всегда положителен, то наибольшему значению функции соответствует наименьшее значение знаменателя. При этом функцию $∘ ---------- ∘ ---------- g(x)= (x+ 1)2+ 22+ (x+3)2+ 32$ можно трактовать как сумму двух расстояний: от точки $(x;0)$ до точки $A(−1;2)$ и от точки $(x;0)$ до точки $B(−3;− 3)$ . Мы специально выбрали точки так, что они лежат по разные стороны от оси абсцисс, тогда наименьшее значение суммы достигается в точке пересечения прямой $AB$ и оси абсцисс. Это будет точка $x= − 95$ , но вычислять ее нет необходимости, так как наименьшее значение функции просто равно длине отрезка

∘-------------- AB = (3− 1)2+ (3 +2)2 = √29.

Поэтому наибольшим значением функции $f(x)= g1(x)$ является $√129$ . Значит,

√a≥ √1- 29

a≥ -1 29

Ответ:

$( 1-;+∞) 29$

Ошибка.
Попробуйте повторить позже

Задача 13#92005

Найдите минимальное значение выражения

∘ -----2---2 ∘ -2-------2 (x+ 6) + y + x + (y − 4)

при условии $2|x|+ 3|y|= 6$ .

Показать ответ и решение

Заметим, что выражение из условия есть сумма расстояний от точки с координатами $(x,y)$ до точек $(−6,0)$ и $(0,4)$ . А уравнение $2|x|+ 3|y|= 6$ задаёт ромб. Наша задача свелась к нахождению точки на границе ромба с минимальной суммой расстояний до двух выбранных. Докажем, что этот минимум достигается в точке, равноудаленной от точек $(−6,0)$ и $(0,4)$ .

Пусть точка $G$ лежит на прямой $l$ , параллельной $EF$ , и удаленной от прямой $EF$ на расстояние $h$ . Пусть также точка $H$ на прямой $l$ такова, что $EH =FH$ , а точка $P$ симметрична $F$ относительно прямой $l$ . Тогда получаем

EG + FG ≥EH + HP = EH + HF.

Причем равенство получается только, если точки $G$ и $H$ совпадают.

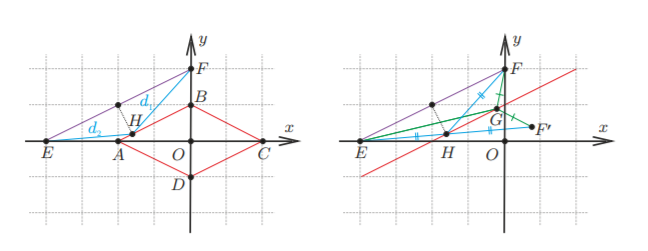
В нашем случае сторона ромба $AB$ параллельна $EF$ , а точка $H$ на прямой $AB$ , для которой $EH = FH$ , лежит на стороне ромба. Сумма расстояний от любой другой точки ромба до точек $E$ и $F$ больше $EH + FH$ . Остается найти $EF$ и расстояние между прямыми $EF$ и $AB$ . Применяя теорему Пифагора, получаем $√ ------ √-- EF = 16+36= 2 13$ . Расстояние между прямыми равно расстоянию от прямой $AB$ до начала координат, поэтому

h⋅AB = AO⋅BO,

откуда $h =√6-- 13$ .

Таким образом,

∘ 36---- ∘205 EH + FH =2 13 + 13= 2-13

Ответ:

$2∘ 205 13$

Ошибка.
Попробуйте повторить позже

Задача 14#91961

Найдите наименьшее значение выражения

∘-----2--- ∘-2---2 ∘-----2--- (x− 9)+ 4+ x + y + (y− 3)+ 9.

Показать ответ и решение

Пусть $A(0,0)$ , $B(x− 9,2)$ , $C(−9,2+y)$ , $D(−12,5)$ . Заметим, что

∘-----2--- ∘ -2--2- ∘ ----2---- ∘--2---2 (x− 9) +4+ x +y + (y− 3) +9= AB + BC +CD ≥ AD = 12 + 5 =13

Осталось показать, что значение $13$ достигается. Для этого точки должны лежать на одной прямой. Значит, $(x− 9):2= −9:(2+y)= −12:5$ , $24 21 x= 9− 5 = 5$ и $45 21 y = 12 − 2= 12$ . Тогда $A (0,0)$ , $24- B (− 5 ,2)$ , $45- C(−9,12)$ , $D(−12,5)$ , эти точки лежат на прямой и именно в таком порядке. Значит, $AB + BC +CD = AD$ .

∘--------- ∘ ------ ∘--------- (x− 9)2 +4+ x2 +y2+ (y− 3)2 +9.= 5.2+ 4.55+3.25= 13

Ответ: 13

Предыдущий раздел

Следующий раздел