Геометрическая вероятность

Случай прямая пересекает стороны квадрата

Пусть — проекции на стороны а в точках прямая пересекает эти стороны.

Если то а прямая делит квадрат на равные треугольники площадью по Поэтому точки различны, прямая делит квадрат на треугольник и пятиугольник:

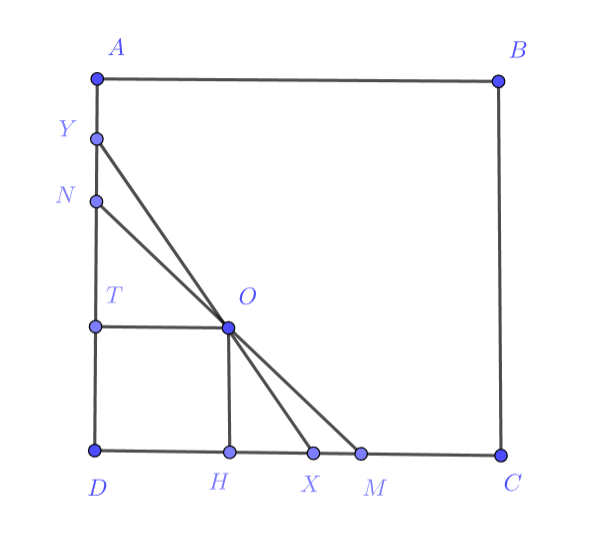
Обозначим С учётом и подобия получаем Запишем условие на площадь:

Мы выяснили, что нам подходят

и как раз соответствуют случаям, когда проходит через и и соответственно.

Случай прямая пересекается только с одной из сторон то есть делит квадрат на два четырёхугольника.

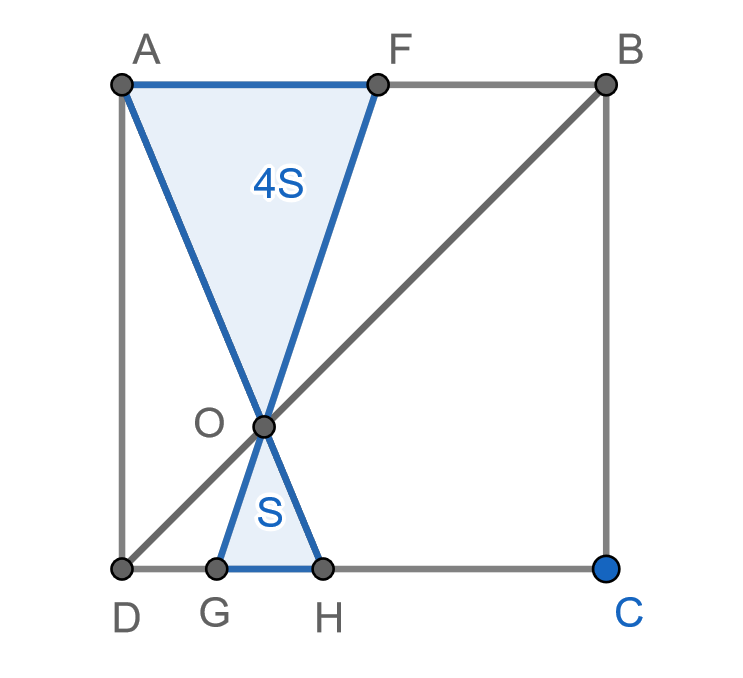
Покажем, что в таком случае площадь обоих частей Выше мы уже заметили, что в случае совпадения прямой с прямой или в случае совпадения с прямой площадь меньшей из отсекаемых частей в точности равна

Предположим, что прямая пересекает стороны Пусть она пересекает в точке в точке Треугольники подобны, при этом коэффициент подобия равен поэтому

Заметим, что если мы перейдем от прямой к прямой то площадь меньшей из частей увеличится на Но так как площадь то площадь

Случай, если пересекает стороны разбирается аналогично (просто рассматривается прямая вместо ).

В результате получаем ответ

Можно в числителе применить формулу разности арктангенсов