Тема САММАТ (Самарская математическая олимпиада)

Уравнения, неравенства и системы на САММАТе

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела саммат (самарская математическая олимпиада)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#74902Максимум баллов за задание: 7

Докажите, что для положительных $a$ и $b$ имеет место неравенство

√ - √3- 5√-- 2 a+3 b≥ 5 ab

Подсказки к задаче

Подсказка 1

У нас стоят коэффициенты 2 и 3, а справа стоит 5..Наверное, нужно как-то применить нер-во о средних к пяти числам, а не к двум..

Подсказка 2

Разбейте 2 и 3 как 1+1 и 1+1+1)

Показать доказательство

Применим неравенство о средних для пяти чисел (они положительные):

√- 3√- √- √ - 3√- 3√- 3√- 5√ -- 2 a+ 3 b= a + a+ b+ b+ b ≥5 ab

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#88702Максимум баллов за задание: 7

Пусть $z,u,v$ — положительные числа. При каких ограничениях на $z,u,v$ существует конечное число положительных целых чисел $(x,y),$ удовлетворяющих неравенству

y x vu < z?

Источники: САММАТ - 2024, 11.1 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

Не совсем понятно, как работать с неравенством в таком виде, попробуем его хоть как-то преобразовать. Что можно сделать с обеими частями?

Показать ответ и решение

Прологарифмируем это неравенство:

lnv+ ylnu< xlnz =⇒ ylnu< xln z− lnv.

получили неравенство для линейной функции.

Для того, чтобы пары $(x,y)$ были целыми положительными числами, график должен располагаться в первой четверти так, как это показано на рисунке, а интересующая нас область — заштрихована.

$PIC$

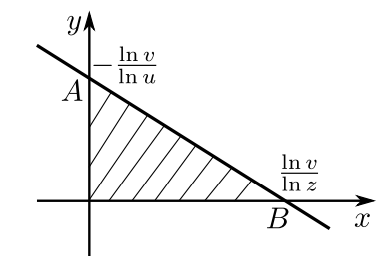
Пусть $lnu >0$ , тогда имеем $y < lnzx− lnv lnu lnu$ (эта ситуация изображена на рисунке). Если $ln u> 0$ , $u > 1$ , то $− lnv->0 lnu$ и $lnv> 0 lnz$ , откуда $0< v < 1$ и $0< z < 1$ .

Случай $ln u< 0$ при любых $lnz$ и $ln v$ задаёт неограниченную область изменения $(x,y)$ , он не реализуем по условию задачи.

Ответ:

$u >1,0< v < 1,0 <z <1$

Ошибка.
Попробуйте повторить позже

Задача 3#88712Максимум баллов за задание: 7

Решить уравнение

∘ √------√-------√-- 4√----- 4√----- 4√- 2x− 1+ 3x− 1 − x− 2x− 1− 3x− 1+ x= 0

Источники: САММАТ - 2024, 11.10 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

Внимательно посмотрим на уравнение. Есть много похожих слагаемых, что можно сделать для удобства?

Подсказка 2

Замену! Попробуем избавиться от корней и заменить корни 4-й степени. Как можно работать с получившимся уравнением?

Подсказка 3

С одной стороны корень, с другой стоит число, поэтому возведем обе части в квадрат! Что получим после преобразований?

Подсказка 4

0 = c^2 + ab - ac - bc. Остается лишь вспомнить, к чему мы стремимся, когда с одной стороны уравнения стоит 0, и решить его!

Показать ответ и решение

Обозначим корни четвёртых степеней через $a,b$ и $c$ , тогда уравнение примет вид:

∘ -2--2---2 a +b − c = a+b− c

После возведения в квадрат и приведения подобных получаем равенство

0= c2 +ab− ac− bc,

что равносильно

(c− b)(c− a)= 0,

откуда либо $c= b$ , то есть $x = 12$ , либо $c= a$ , откуда $x =1$ .

При подстановке оба корня подходят (её необходимо сделать, потому что при возведении в квадрат могли появиться лишние корни).

Ответ:

$1 ;1 2$

Ошибка.
Попробуйте повторить позже

Задача 4#69930Максимум баллов за задание: 7

Найти решение уравнения в натуральных числах $x$ и $y :$

∘ 2---2------------ ∘-2---2------------ x +y − 2x− 6y +10+ x + y − 18x − 6y+ 90− 10 =0

Источники: САММАТ-2023, 11.7 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

У нас в задаче присутствует равенство √a+√b=c. Хочется возвести в квадрат, но, если возводить прямо так, у нас получится произведение корней √ab. Поэтому разумно было бы перенести один корень направо и возвести в квадрат...

Подсказка 2

После возведения в квадрат и приведения подобных, можно оставить корень в одной стороне, а все остальное отправить в другую и опять возвести в квадрат. Можно ли как-то после этого удачно сгруппировать слагаемые?

Подсказка 3

Получается следующее: (x-5)²/5²+(y-3)²/3²=1. Но тогда |x-5|≤5 и |y-3|≤3 ⇔ 0≤x≤10 и 0≤y≤6. Осталось перебрать x и y и найти искомые решения!

Показать ответ и решение

Если выделить полные квадраты под корнями, то уравнение можно записать в виде

∘-------------- ∘-------------- (x− 1)2+ (y− 3)2+ (x− 9)2+ (y− 3)2 = 10

Этому уравнению удовлетворяют такие пары точек $(x,y)$ , сумма расстояний от которых до точек $(1,3)$ и $(9,3)$ равна $10.$

Множеством точек плоскости, обладающих таким свойством, является эллипс. По его фокусам легко восстановить канонический вид уравнения (центр эллипса находится в середине между фокусами, координаты считаются как полусумма, соответственно считаются и длины больших полуосей):

(x− 5)2 (y− 3)2 --52--+ --32-- =1

Перебором $5≤ x≤ 10$ и $3≤y ≤6$ можно найти решения $(5,6)$ и $(10,3)$ , а им из симметрии соответствуют пары $(5,0)$ и $(0,3)$ . В ответ же записываем только пары, у которых обе компоненты натуральные.

Ответ:

$(10,3),(5,6)$

Ошибка.
Попробуйте повторить позже

Задача 5#74946Максимум баллов за задание: 7

Решите неравенство:

( (-x-))2020 ( ( -x-))2022 2022 4 1− ln 2021 + 1+ ln 2021 ≥ 2

Источники: САММАТ-2022, 11.2 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

Очень напрашивается замена страшного логарифма, поэтому давайте будем доверять своим желаниям и сделаем её. Пусть это t. Тогда так как при t = ±1 получается равенство, можно рассмотреть случаи расположения t относительно -1 и 1

Подсказка 2

Можно воспользоваться знанием про равенство при |t| = 1 и оценить левую часть при помощи этого.

Подсказка 3

Сразу сумму скобочек неудобно оценивать, но их можно оценить по отдельности: в каждом из случаев получается, что каждая скобочка больше или меньше 2 в какой-то степени, а в сумме удачно получается 2²⁰²²! А дальше не забываем про обратную замену и выписываем нужные х в ответ

Показать ответ и решение

Пусть $t= ln (-x-) , 2021$ тогда

2020 2022 2022 4(1− t) + (1+t) ≥ 2

Рассмотрим случаи:

$1)$

2020 2022 2022 2022 t≥ 1⇒ 4(1− t) +(1+ t) ≥ (1 +t) ≥2

$2)$

t≤ −1⇒ 4(1− t)2020+(1+ t)2022 ≥ 4(1 − t)2020 ≥22022

$3)$

−1< t< 1

( ( ) ( ) ) 4(1− t)2020+ (1+ t)2022 =22022 1−-t 2020+ 1+-t 2022 < 2 2

( 1− t 1+t) <22022 -2--+ -2-- = 22022

Так как

0< 1−-t<1, 0< 1+-t< 1 2 2

при $− 1< t<1.$

Следовательно, при $− 1< t< 1$ неравенство не выполнятся.

Тогда

⌊ ln(-x-) ≥ 1 |⌈ (2021) ln -x-- ≤ −1 2021

( ] x ∈ 0;2021- ∪[2021e;+ ∞) e

Ответ:

$(0;2021]∪ [2021e;+∞ ) e$

Ошибка.
Попробуйте повторить позже

Задача 6#74949Максимум баллов за задание: 7

Решить уравнение

∘-2------- ∘-2--- 3√---- √3----- x + 4x− 2− x + 6= x +3− 3x − 1

Источники: САММАТ-2022, 11.5 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

Преобразуем равенство так, чтобы получилось равенство сумм, а после - попробуем рассматривать обе части равенства как функции. Что интересного можно заметить?

Подсказка 2

Заметим, что обе части можно выразить как одну и ту же функцию, но от разных переменных: от 3 и 2x - 1. Попробуем тогда исследовать функцию и найти ее корни!

Подсказка 3

Функция оказывается монотонной...подумаем, что же это означает)

Показать ответ и решение

Обозначим функции

∘-2---- 3√---- F (x,y)= x + 2y+ x+ y, g(x) =3, h(x)= 2x − 1,

тогда

∘-2--- 3√---- ∘-2------- 3√----- F (x,g(x))= x + 6+ x +3, F (x,h(x))= x + 4x− 2+ 3x− 1

Поэтому исходное уравнение можно записать в виде

∘x2+-4x−-2− ∘x2+-6= 3√x-+3− √33x-− 1

F(x,g(x))= F(x,h(x))

Пусть $x0$ — корень исходного уравнения, тогда $x0$ также является корнем уравнения

F (x0,g(x))= F(x0,h(x))

Но так как функция

∘------ √----- f(y)=F (x0,y)= x20+ 2y+ 3x0+ y

является строго возрастающей по переменной $y$ при всех $x2 y ≥ −-02 ,$ тогда полученное уравнение равносильно уравнению

F(x0,g(x))= F (x0,h(x))⇔ g(x)= h(x)

2x− 1= 3⇔ x0 = 2

Нетрудно проверить, что $x0 = 2$ попадает в область допустимых значений и является корнем исходного уравнения:

∘ 2--------- ∘-2--- √-- √-- 3√- √3- 3√---- 3√------ 2 +4⋅2− 2− 2 + 6= 10− 10= 0= 5 − 5= 2+ 3− 3 ⋅2 − 1

Ответ: 2

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#74950Максимум баллов за задание: 7

Докажите, что для $a< 1,b<1,c< 1,a +b+ c≥ 1 2$ выполняется неравенство

125- (1 − a)(1− b)(1− c)≤ 216

Источники: САММАТ-2022, 11.6 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

Нам дали неравенство на сумму чисел, а попросили доказать неравенство про произведение. Какое известное неравенство можно попробовать применить?

Подсказка 2

Верно, неравенство о среднем арифметическом и среднем геометрическом! Но в нём извлекают корень из произведения, поэтому давайте тоже его извлечём, а потом обратно в куб возведём

Показать доказательство

Так как $a< 1,b <1,c< 1,$ то $1− a >0,1− b >0,1− c >0.$ Используя известное неравенство о средних, получим

3∘--------------- (1− a)+-(1-− b)+-(1−-c) a+-b+c- 5 (1− a)(1− b)(1− c)≤ 3 = 1− 3 ≤6

при условии, что $1 a+ b+c≥ 2.$

Следовательно, получили

∘ --------------- 5 3 (1− a)(1− b)(1− c)≤ 6

Возведём в куб последнее неравенство и получим требуемое неравенство.

Ошибка.
Попробуйте повторить позже

Задача 8#74952Максимум баллов за задание: 7

Решите систему уравнений

(| √yz ||||| x = y+-z ||{ √xz || y = x+-z ||||| √yx |( z = y+-x

Источники: САММАТ-2022, 11.8 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

Система циклическая, поэтому попробуем найти какие-то «парные» решения и поставим какие-нибудь ограничения на переменные. Что нам напоминает правая часть каждого из уравнений?

Подсказка 2

Заметим, что сменив знак у каждой из переменных, тройка остается решением. Значит, мы можем считать, что все переменные положительны. А правая часть каждого из уравнений напоминаем нам неравенство о средних! Тогда попробуем лучше оценить каждую из переменных)

Подсказка 3

Заметим, что каждая из переменных не больше 1/2(почему?). Теперь хочется как-то связать равнения системы…а что если выполнить преобразования, после которых мы сможем что-то сократить? Обратим внимание на наличие корня в числителях! Остается дело за малым)

Показать ответ и решение

Отметим, что числа $x,y,z$ одного знака, при этом если тройка $(x;y;z)$ — решение системы, то $(−x;− y;−z)$ также решение.

Пусть числа $x,y,z$ положительны. Из неравенства о средних

√ -- a+ b≥2 ab

следует, что

√ab- 1 a+ b ≤ 2

Следовательно, каждое из чисел числа $x,y,z$ не больше $1 2.$

Перемножив все уравнения системы, получим

(x+ y)(y+ z)(z+ x)= 1

Но сумма любых двух из чисел $x,y,z$ не превосходит 1. Следовательно,

x +y = y+ z = z+ x= 1

Значит $x =y =z = 1. 2$ Так как $(−x;−y;−z)$ также будет решением, то $x =$ $y =z =− 1. 2$

Ответ:

$(1;1;1), (− 1;− 1;− 1) 2 2 2 2 2 2$

Ошибка.
Попробуйте повторить позже

Задача 9#106533Максимум баллов за задание: 7

Четыре положительных числа $a,b,c,d$ таковы, что $ab+ cd= ac+bd= 4$ и $ad+bc= 5.$ Найдите наименьшее возможное значение суммы $a+ b+ c+d.$

Подсказки к задаче

Подсказка 1

В этой задаче нам надо как-то оценить сумму. Какое известное неравенство для оценки суммы чисел сразу приходит в голову?

Подсказка 2

Правильно, неравенство о средних! Среднее арифметическое чисел не меньше их среднего геометрического! Однако, если мы запишем неравенство о средних для чисел a, b, c, d, то в одной части получится искомая сумма, а в другой что-то непонятное. Давайте попробуем по-другому: у каких ещё чисел сумма будет равна a+b+c+d?

Подсказка 3

Например, у чисел (a+b) и (c+d). Запишите для них неравенство о средних и не забудьте применить равенства из условия!

Показать ответ и решение

Используя неравенство о средних, получим

∘ ---------- √------------- √---- a+ b+ c+d ≥2 (a+ b)(c+ d)=2 ac+ ad+ bc+ bd= 2 4+ 5= 6.

Равенство достигается при $a= d= 1,b= c=2$ . Все условия задачи выполняются.

Ответ: 6

Ошибка.
Попробуйте повторить позже

Задача 10#94200Максимум баллов за задание: 7

Решить уравнение

∘ ----√------- 5+ 35 − 2 45− 2x= x

Источники: САММАТ - 2021, 11.5 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

Неудобно работать с двумя корнями, давайте заменим тот, что внутри! Подумаем, а как тогда выглядит правая часть уравнения?

Подсказка 2

Если y = √ (45-2x), то правая часть равна 35 - y² . Если бы мы решали уравнение относительно y, как бы мы выразили 35?

Подсказка 3

Или 35 = y² + 2y, или же 35 = y² - 2y - 4 при y≤a!

Показать ответ и решение

Введём замену $y = √45−-2x$ . Тогда получим уравнение

∘ ------ 2 2 35− 2y = 35− y.

Искусственно введем параметр $a$ , заменив 35 на $a$ :

∘ ----- 2 2 a− 2y = a− y .

Решив относительно параметра, получим

a= y2+ 2y или a= y2− 2y − 4 при y ≤ a.

3 Таким образом, получим два уравнения

y2+ 2y = 35 и y2− 2y− 4= 35.

Первое уравнение имеет корни $− 7< 0$ и $5$ (ему отвечает $x =10$ ). Второе уравнение имеет корни $√-- 1− 40< 0$ и $√-- √ -- 1+ 40> 35$ .

Ответ: 10

Ошибка.
Попробуйте повторить позже

Задача 11#94202Максимум баллов за задание: 7

Найдите все пары целых чисел, удовлетворяющих системе неравенств

{ y3− 3x2− 4y +18x− 26 >0, y3+ x2− 4y − 8x+ 14< 0.

Источники: САММАТ - 2021, 11.10 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

Подумаем, как упростить систему, чтобы решать неравенство относительно одной переменной?

Подсказка 2

Домножим первое неравенство на -1 и сложим со вторым! Какими будут целые корни у получившегося неравенства?

Подсказка 3

После того, как мы найдем целые значения x, удовлетворяющие получившемуся квадратному неравенству, можно подставить их в исходную систему и найти y!

Показать ответ и решение

Умножим первое неравенство на $(−1)$ , сложим и получим

2 2 4x − 26x+40 <0 ⇒ 2x − 13x+ 20 <0 ⇒ (D = 9)x ∈(2,5;4).

Единственное целое значение $x$ , удовлетворяющее неравенству, $x =3$ . Подставим $x= 3$ в исходную систему

{ y3− 27− 4y+ 54− 26 >0, { y3− 4y+ 1> 0, { y3 >4y− 1, y3+ 9− 4y − 24+ 14< 0. ⇒ y3− 4y− 1< 0. ⇒ y3 <4y+ 1.

Двойному неравенству удовлетворяют только три целых значения $y :0,− 2,2$ . Сделав проверку, получим, что система имеет три целых решения: $(3;0),(3;2),(3;−2)$ .

Ответ:

$(3;0),(3;2),(3;−2)$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#99090Максимум баллов за задание: 7

Докажите неравенство

---x---- ---y--- ---z--- −x+ y+ z + x− y+ z + x+ y− z ≥ 3,

где $x,y,z$ — стороны произвольного треугольника.

Показать доказательство

Заметим, что в знаменателях стоят длины отрезков касательных к вписанной в треугольник со сторонами $x,y,z$ окружности. Обозначим знаменатели $a,b,c.$ Тогда неравенство эквивалентно

b+ c c+ a a+ b -2a-+ -2b-+ -2c-≥ 3

b c c a a b a +-a +-b +-b-+-c +-c≥ 1 6

Последнее верно в силу неравенства между средним арифметическим и средним геометрическим для 6 чисел (положительных, так как это длины отрезков касательных).

Ошибка.
Попробуйте повторить позже

Задача 13#98022Максимум баллов за задание: 7

Переменные $x,y,z,t$ таковы, что справедливо неравенство