.06 Кривизна траектории

Нормальное ускорение точки, движущейся на ободе колеса можно выразить через скорость этой точки:

где - радиус кривизны траектории.

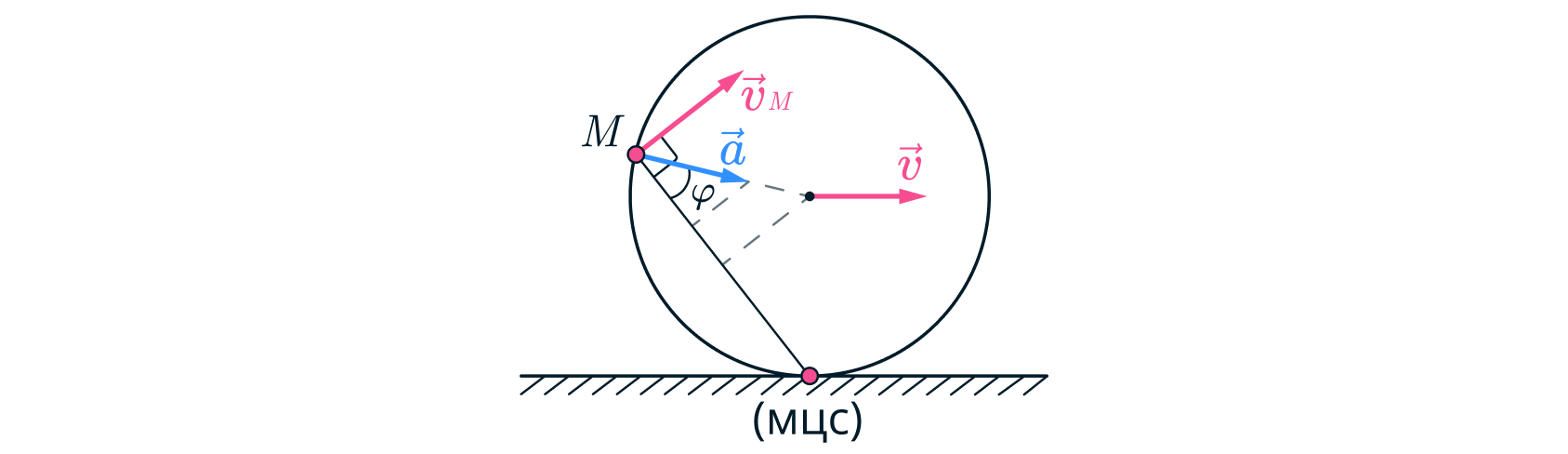
Теперь выразим нормальное ускорение через полное ускорение точки, направленное в центр колеса:

А полное ускорение в свою очередь можно выразить из вращательного движения точки вокруг центра окружности:

где - радиус колеса. Теперь выразим скорость вращения точки относительно центра колеса в СО центра колеса, чтобы получить выражение для .
Из теоремы Пифагора:

Подставим в формулу (1) выражения для ускорения и скорости точки М:

Сократим некоторые величины:

Заметим, что проецируя радиус окружности на отрезок, соединяющий точку и МЦС, получим:

Отсюда:

ч.т.д.