.06 Кривизна траектории
Ошибка.
Попробуйте повторить позже
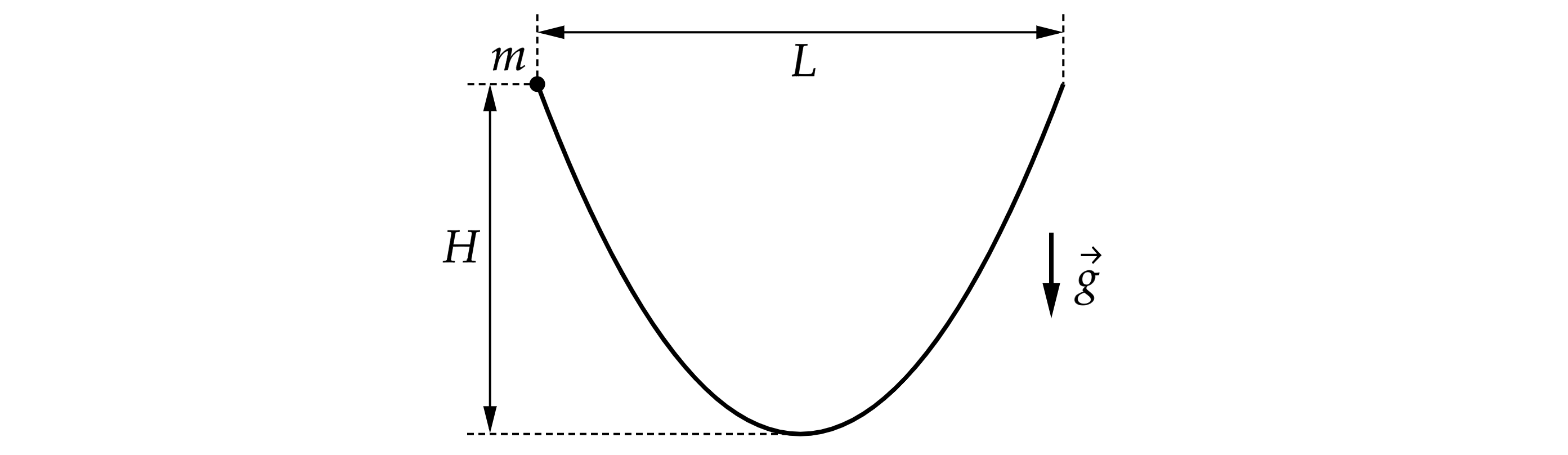
Отрезок проволоки изогнут в виде симметричного участка параболы и расположен так, что ось её симметрии вертикальна.
На этот отрезок надевают маленькую бусинку массой , удерживая её у одного из краёв проволоки. Затем
бусинку отпускают без начальной скорости, и она начинает скользить по проволоке под действием силы
тяжести. Найдите модуль силы, с которой бусинка будет давить на проволоку, находясь в самой нижней
точке своей траектории. Трение пренебрежимо мало. Размеры
и
, указанные на рисунке, известны.
(МОШ, 2015, 10)
Источники:
Первый способ:
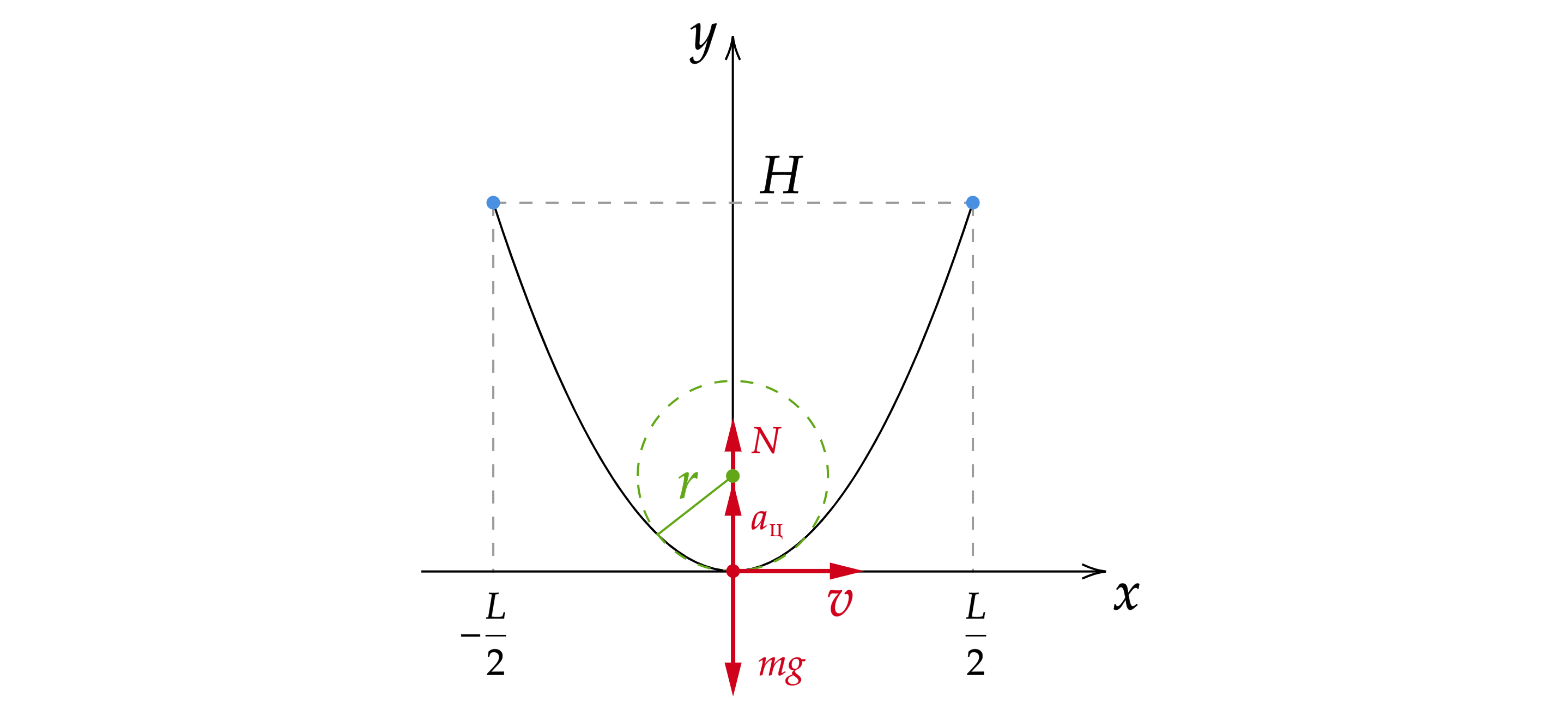
Расставим силы действующие на бусинку в нижней точке (сила нормальной реакции опоры, сила тяжести). Также на
бусинку будет действовать центростремительное ускорение, направленное в центр окружности, радиус которой равен
радиусу кривизны параболы в этой точке.
Запишем второй закон Ньютона в проекции на ось для бусинки:
С учётом центростремительного ускорения:
По третьему закону Ньютона сила давления бусинки на стержень будет равна силе нормальной реакции опоры:
Скорость бусинки в этой точке можно найти из закона сохранения энергии:
Следовательно,
Для кривой на плоскости можно ввести понятие кривизны. Это величина обратно пропорциональна радиусу кривизны и равна:
В данной задаче, отрезок проволоки является параболой. Поместим параболу в начале координат (см. рис.).
Тогда парабола будет описываться уравнением: . Используя
и
найдём коэффициент
:
Далее используя уравнение кривизны получим выражение:
Когда бусинка будет находится в нижней точке, то координата будет равна нулю:
Тогда радиус кривизны будет равен:
Подставляя в выражение для силы давления, в итоге получим:
Второй способ:
Данный способ позволяет решить задачу без знания уравнения кривизны. Из первого способа мы знаем уравнение нашей
параболы:
Исходя из того, что:
Получим следующее (в общем виде):
Так как бусинка находится в нижней точке, то составляющая ускорения по оси отсутствует (
). Также
отсутствует составляющая скорости по оси
(
) и тогда
, где
- скорость, определяемая ЗСЭ (см. в
первом способе).
Тогда уравнение для ускорения будет иметь вид (при ):
И в итоге сила давления на проволоку будет иметь вид:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




