Базовый вариант весеннего тура Турнира Городов

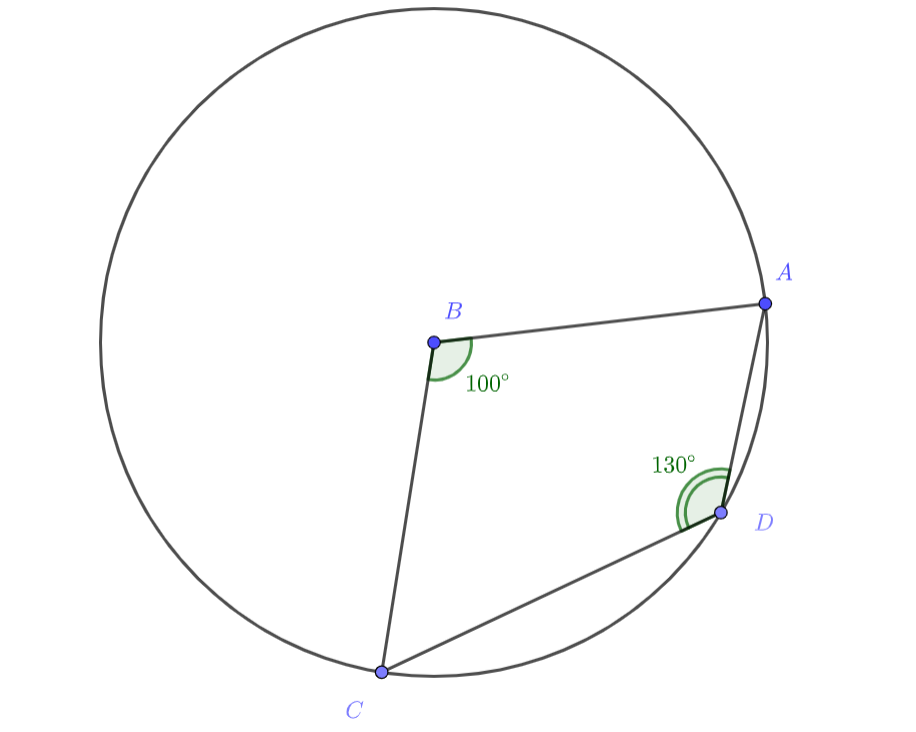
Первое решение.

Построим окружность с центром в точке и радиусом — на ней лежат и . Покажем, что точка также лежит на окружности. Для этого заметим, что градусная мера меньшей дуги равна , а большей — . Точка лежит между и , потому из написанного выше следует, что она лежит на меньшей дуге и вписанный. Отсюда .

Второе решение.

Из равнобедренности . Для с радиусом описанной окружности применим теорему синусов и получим . Заметим, что лежит на серединном перпендикуляре к и удалён от и на расстояние . Но тогда в силу единственности центра описанной окружности он и будет центром (заметим, что он лежит по противоположную от сторону от вершины , ведь тупой). Отсюда .