Базовый вариант весеннего тура Турнира Городов
Ошибка.
Попробуйте повторить позже
Хорды 
и 
окружности с центром 
пересекаются в точке 
Пусть 
и 
— центры описанных окружностей треугольников
и 
соответственно. Докажите, что 
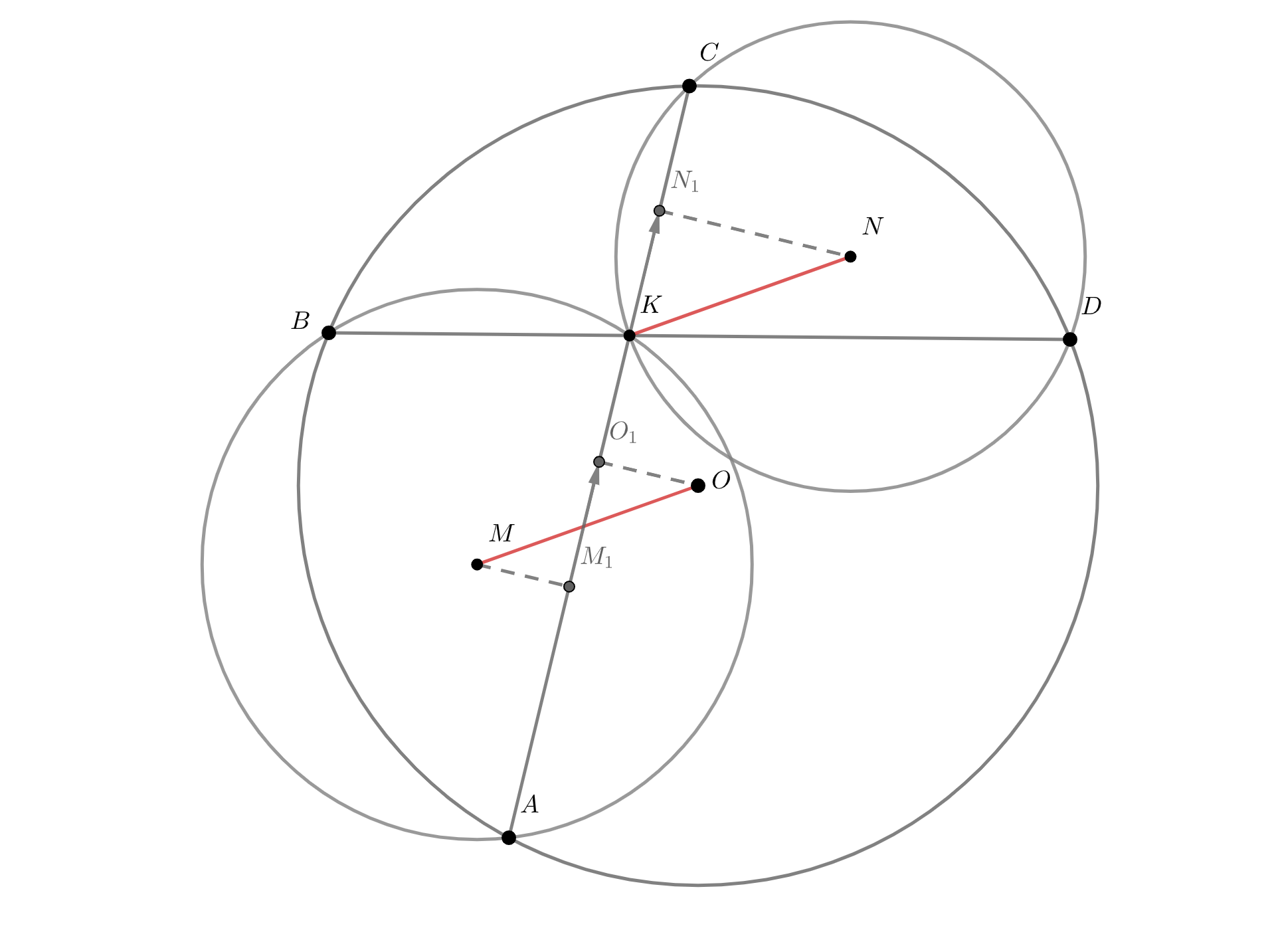
Рассмотрим проекции 
и 
векторов 
и 
на хорду 
— середина хорды 
, поэтому
и 
— середины хорд 
и 
, поэтому
Таким образом, 
.
Аналогично равны проекции векторов 
и 
на хорду 
. Но вектор полностью определяется своими проекииями на две
непараллельные прямые. Поэтому 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
