.00 №14 из ЕГЭ 2018
Ошибка.
Попробуйте повторить позже
В кубе все ребра равны 6.
а) Докажите, что угол между прямыми и
равен
б) Найдите расстояние между прямыми и
Источники:
а) Отрезки и
равны и параллельны, следовательно,
— параллелограмм и
Тогда угол
между пересекающимися прямыми
и
— это и есть угол между скрещивающимися прямыми
и
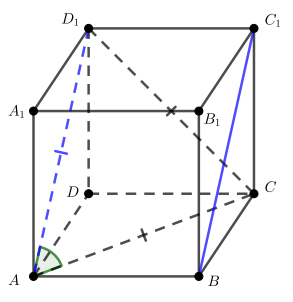
Рассмотрим треугольник Все его стороны являются диагоналями равных квадратов — граней куба. Следовательно,
треугольник
— равносторонний и искомый угол
равен
б) Так как прямые и
скрещиваются, то для нахождения расстояния между ними построим через каждую из
прямых плоскость, параллельную другой прямой. Тогда расстояние между двумя полученными параллельными плоскостями
равно расстоянию между прямыми.
Мы уже доказали, что следовательно, плоскость
содержит
и параллельна
По
аналогичным соображениям плоскость
параллельна прямой
и плоскости
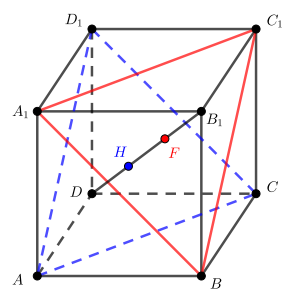
Пусть — точка пересечения прямой
с плоскостью
а
— точка пересечения прямой
с плоскостью
Тогда если прямая
перпендикулярна паре параллельных плоскостей, то длина отрезка
равна расстоянию
между плоскостями и искомому расстоянию между прямыми.
Докажем, что и найдем длину
Так как диагонали квадрата перпендикулярны, то прямая перпендикулярна проекции
наклонной
откуда по
теореме о трех перпендикулярах имеем
Пусть
— точка пересечения
и
Несложно видеть, что точка
пересечения прямой
и плоскости
также является точкой пересечения прямых
и
в плоскости
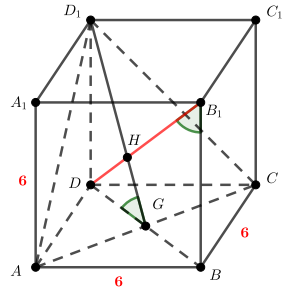
Диагональ квадрата со стороной 6 равна тогда
Также по теореме Пифагора для
треугольника
Рассмотрим прямоугольный треугольник
Рассмотрим прямоугольный треугольник
Оба угла острые, значит, равенство тангенсов влечет равенство самих углов.
Рассмотрим треугольники и
У них
— общий, следовательно,
В итоге прямая перпендикулярна прямым
и
а значит, перпендикулярна плоскости
Найдем
длину
как высоту в прямоугольном треугольнике
Из соображений симметрии плоскость отсекает от диагонали
куба отрезок
равный
Общая длина
диагонали равна
значит, оставшаяся средняя часть диагонали равна
Как было доказано, длина этого отрезка равна искомому расстоянию между прямыми и
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




