№14 из ЕГЭ 2018
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
В цилиндре на окружности нижнего основания отмечены точки и
На окружности верхнего основания отмечены точки
и
так, что
является образующей цилиндра, перпендикулярной основаниям, а
пересекает ось
цилиндра.
а) Докажите, что прямые и
перпендикулярны.
б) Найдите расстояние между прямыми и
если
Источники:
а) Пусть — проекция точки
на плоскость нижнего основания. Так как
пересекает ось
цилиндра, то
лежит
в плоскости осевого сечения цилиндра, следовательно,
— диаметр нижнего основания.
Так как и
— перпендикулярные основаниям образующие, то
— параллелограмм и
Тогда
угол
между прямыми
и
— это и есть по определению угол между скрещивающимися прямыми
и
С учетом того, что
— диаметр, получаем
как вписанный угол, опирающийся на
диаметр.
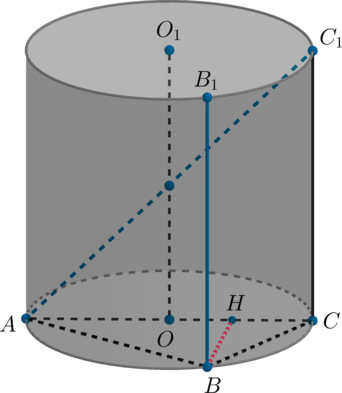
б) Заметим, что прямые и
являются скрещивающимися, так как
а
Расстояние между скрещивающимися прямыми в таком случае равно расстоянию от любой точки прямой
до плоскости
Проведем
в плоскости
Так как высота цилиндра
то
Таким образом, мы имеем две прямые в плоскости которые перпендикулярны прямой
Значит,
—
расстояние от точки
до плоскости
то есть искомое расстояние.
Так как и
— параллелограмм, то
Тогда по теореме Пифагора в треугольнике
Тогда запишем площадь треугольника двумя способами и найдем
Таким образом,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В кубе все ребра равны 6.
а) Докажите, что угол между прямыми и
равен
б) Найдите расстояние между прямыми и
Источники:
а) Отрезки и
равны и параллельны, следовательно,
— параллелограмм и
Тогда угол
между пересекающимися прямыми
и
— это и есть угол между скрещивающимися прямыми
и
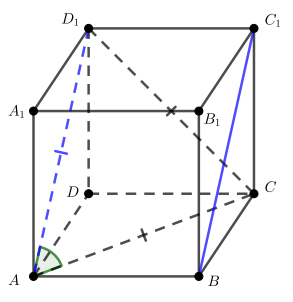
Рассмотрим треугольник Все его стороны являются диагоналями равных квадратов — граней куба. Следовательно,
треугольник
— равносторонний и искомый угол
равен
б) Так как прямые и
скрещиваются, то для нахождения расстояния между ними построим через каждую из
прямых плоскость, параллельную другой прямой. Тогда расстояние между двумя полученными параллельными плоскостями
равно расстоянию между прямыми.
Мы уже доказали, что следовательно, плоскость
содержит
и параллельна
По
аналогичным соображениям плоскость
параллельна прямой
и плоскости
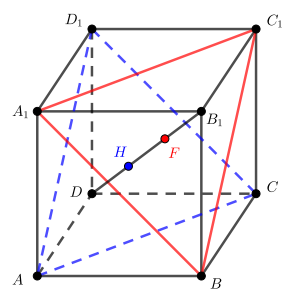
Пусть — точка пересечения прямой
с плоскостью
а
— точка пересечения прямой
с плоскостью
Тогда если прямая
перпендикулярна паре параллельных плоскостей, то длина отрезка
равна расстоянию
между плоскостями и искомому расстоянию между прямыми.
Докажем, что и найдем длину
Так как диагонали квадрата перпендикулярны, то прямая перпендикулярна проекции
наклонной
откуда по
теореме о трех перпендикулярах имеем
Пусть
— точка пересечения
и
Несложно видеть, что точка
пересечения прямой
и плоскости
также является точкой пересечения прямых
и
в плоскости
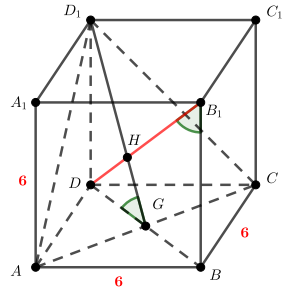
Диагональ квадрата со стороной 6 равна тогда
Также по теореме Пифагора для
треугольника
Рассмотрим прямоугольный треугольник
Рассмотрим прямоугольный треугольник
Оба угла острые, значит, равенство тангенсов влечет равенство самих углов.
Рассмотрим треугольники и
У них
— общий, следовательно,
В итоге прямая перпендикулярна прямым
и
а значит, перпендикулярна плоскости
Найдем
длину
как высоту в прямоугольном треугольнике
Из соображений симметрии плоскость отсекает от диагонали
куба отрезок
равный
Общая длина
диагонали равна
значит, оставшаяся средняя часть диагонали равна
Как было доказано, длина этого отрезка равна искомому расстоянию между прямыми и
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильном тетраэдре точка
— центр грани
а точка
— середина ребра
а) Докажите, что прямые и
перпендикулярны.
б) Найдите угол между прямыми и
Источники:
а) Проведем медианы и
в треугольниках
и
соответственно. Тетраэдр правильный, следовательно, его
грани — равносторонние треугольники и медианы будут также являться высотами, то есть
и
Тогда прямая
перпендикулярна двум пересекающимся прямым плоскости
Значит, прямая
перпендикулярна плоскости
и перпендикулярна любой прямой плоскости
в частности, прямой
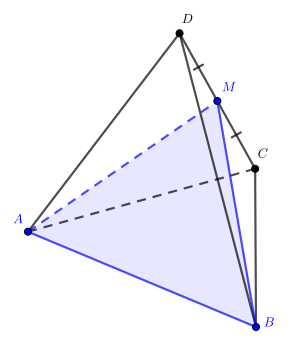
б) Прямая перпендикулярна плоскости
Опустим перпендикуляр
на
Тогда
и
искомый угол между прямыми
и
есть угол между прямыми
и
то есть угол
Обозначим ребро тетраэдра через Тогда высота равностороннего треугольника его грани равна
Посмотрим на медиану треугольника
Точка
— центр треугольника, а значит, и точка пересечения медиан.
Известно, что точка пересечения медиан делит каждую медиану в отношении
считая от вершины, следовательно,
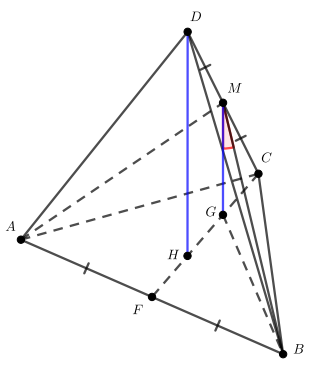
Точка — середина
точка
— проекция точки
на плоскость
Следовательно, проекция точки
на плоскость
— точка
— будет являться серединой
Таким образом,
и
По теореме Пифагора дла треугольника
Отрезок как высота в треугольнике
Тогда из прямоугольного треугольника
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |

