Системы неравенств
Ошибка.
Попробуйте повторить позже
Найдите наибольшее значение выражения при условии
Источники:
Подсказка 1
У нас есть система неравенств с модулем, и нам надо найти наибольшее значение третьего выражения. Попробуем решить графически!
Подсказка 2
Раскроем знак модуля и построим чертеж: неравенства задают полосы, что образует их пересечение?
Подсказка 3
Пересечение задает параллелограмм. Чтобы найти его вершины аналитически, приравняем попарно соответствующие уравнения.
Подсказка 4
Теперь перейдем к уравнению, в котором необходимо найти наибольшее значение: 4x + 8y = C. Как задается на плоскости это уравнение в зависимости от С? Что от нас требуется на графике для выполнения условия?
Подсказка 5
Необходимо определить максимальное значение С, при котором прямая пересекает параллелограмм. Заметим, что при увеличении C прямая движется вверх на плоскости, тогда нам нужно найти такое С, при котором полученная прямая будет касаться параллелограмма в точке с наибольшими координатами.
Данная система неравенств эквивалентна следующим:
Первое неравенство задаёт полосу между параллельными прямыми и
а второе — полосу между прямыми
и
Их пересечением является параллелограмм. Найдем его вершины, решив соответствующие системы линейных
уравнений:
Аналогичным образом находим, что параллелограмм имеет вершины в точках
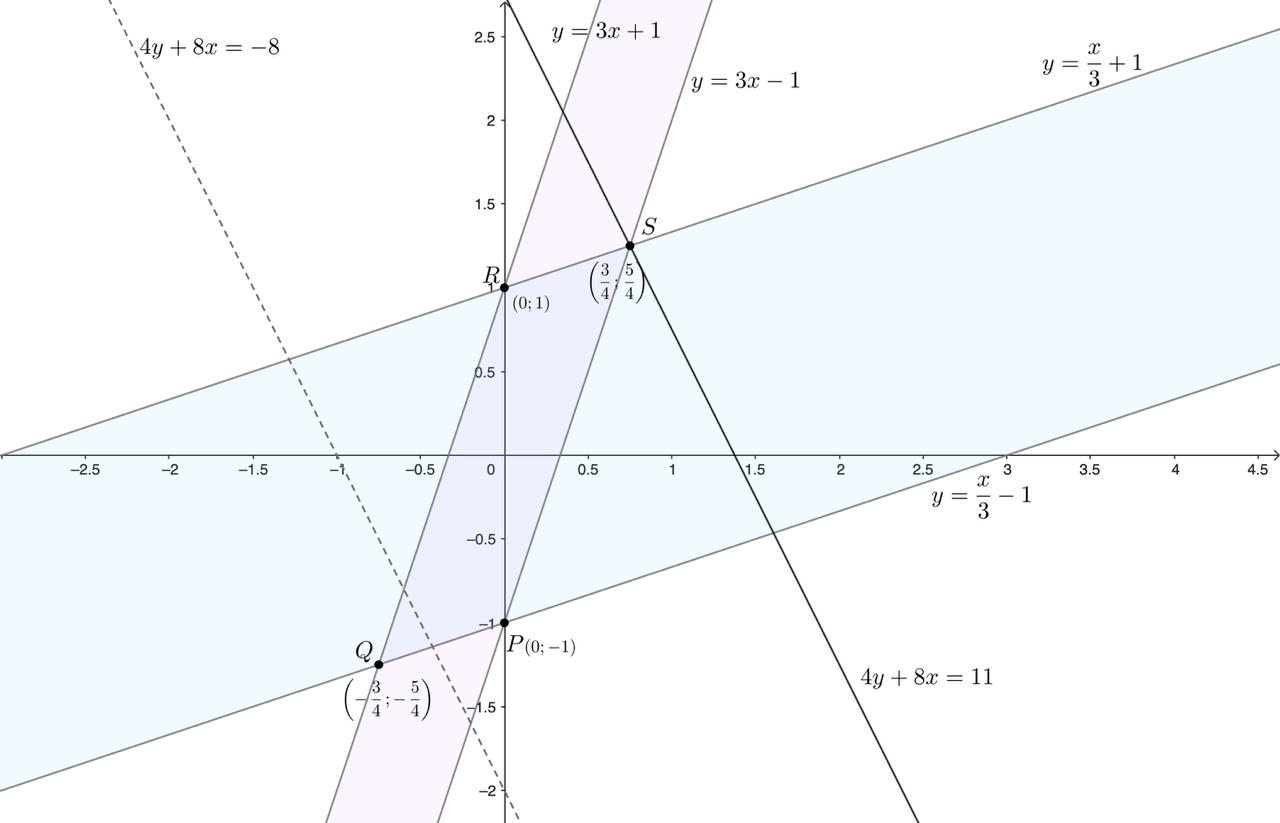
Рассмотрим уравнение где
— некоторая константа. Оно задаёт прямую на плоскости, причём в любой
точке прямой значение выражения
постоянно и равно
Если изменить значение
получится некоторая
другая прямая, на которой выражение
принимает новое значение. Нам необходимо определить максимальное
значение
при котором прямая
пересекает параллелограмм. Несложно увидеть, что при увеличении
прямая движется вверх на плоскости, и самое большое
получается, когда прямая проходит через точку
Это значение
равно:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




