Тема НадЭн (Надежда энергетики)

Функции на Энергетике

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела надэн (надежда энергетики)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#96522

Уравнение $F(x) =0,$ где $F(x)= x2 +px+ q,$ имеет ровно один вещественный корень, а уравнение $F(F(F(x)))=0$ — ровно три вещественных корня. Найдите все эти корни.

Подсказки к задаче

Подсказка 1

Если квадратный трёхчлен имеет один корень, то какой вид он принимает?

Показать ответ и решение

Ясно, что $F(x)$ имеет вид $F(x)= (x− a)2,$ поэтому

(( 2 )2 )2 F(F(F(x)))= (x− a) − a − a =0.

Получаем, что $( 2 )2 (x − a) − a = a >0$ (строгое неравенство $a> 0$ следует из того, что при $a= 0$ уравнение $F(F(F(x)))= 0$ имеет не три, а всего один корень), откуда $2 √- (x − a) = a± a.$

Поскольку у этих двух квадратных уравнений должно быть три корня, у одного из у равнений должен быть один корень, а у другого два. У уравнения $2 √- (x− a)= a+ a$ не может быть всего один корень, так как $√- a+ a> 0,$ поскольку $a> 0.$ Значит, один корень имеет уравнение $√- (x− a)2 =a− a,$ то есть $√- a− a =0,$ что даёт два варианта: $a= 0$ или $a= 1.$ Поскольку $a> 0$ , остаётся только $a =1.$

Теперь, решив уравнения $√- (x− a)2 = a± a$ при $a= 1,$ легко найдём все три корня уравнения $F(F(F(x)))=0 :$ это $√ - x1 = 1,x2,3 = 1± 2.$

Ответ:

$x = 1,x = 1±√2 1 2,3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#96524

Напряжённость электрического поля в точке $(x,y)$ описывается функцией

( )x2+y2 E(x,y)= 2201 .

Найдите максимальное значение напряжённости в области, задаваемой неравенствами

|ax+ y|≤b, |ax− y|≥ b,

где $a$ и $b$ — фиксированные вещественные числа.

Показать ответ и решение

Функция $E (f)= (20)f 21$ монотонно убывает при $f ∈ [0,∞ ).$ Рассмотрим величину $f(x,y)= x2+ y2,$ если переменные удовлетворяют неравенствам

|ax+ y|≤b, |ax− y|≥ b.

Максимум $E$ соответствует минимуму $f.$

1. Если $b <0$ , то множество решений системы неравенств пусто. Функция не определена.

2. Если $b =0$ , то неравенства равносильны уравнению $ax+ y = 0$ , откуда $f(x,− ax)= g(x)= (1+ a2)x2$ . Максимум $E (x,y)$ будет до стигаться в начале координат и будет равен $1.$

3. Пусть $b> 0,a= 0.$ Тогда система неравенств равносильна уравнению $|y|= b$ и $2 2 2 f(x,y)= f(x,|b|)=x +b ≥ b.$ Максимум равен $(20)b2 21 .$

4. Пусть $b> 0,a> 0.$ Тогда получаем систему ограничений

−b− ax ≤y ≤b− ax, (y ≤ ax− b или y ≥ ax+ b).

Она задает на плоскости область между двумя параллельными прямыми $y = −b− ax$ и $y = b− ax$ и вне ромба с вершинами $(0;±b),(±b∕a;0).$ Функция $f$ есть квадрат расстояния от начала координат до точки области. Точки с одинаковым расстоянием от $O$ образуют окружность. Минимум расстояния имеют точки касания сторон ромба со вписанной в ромб окружностью. Найдем ее радиус $r.$

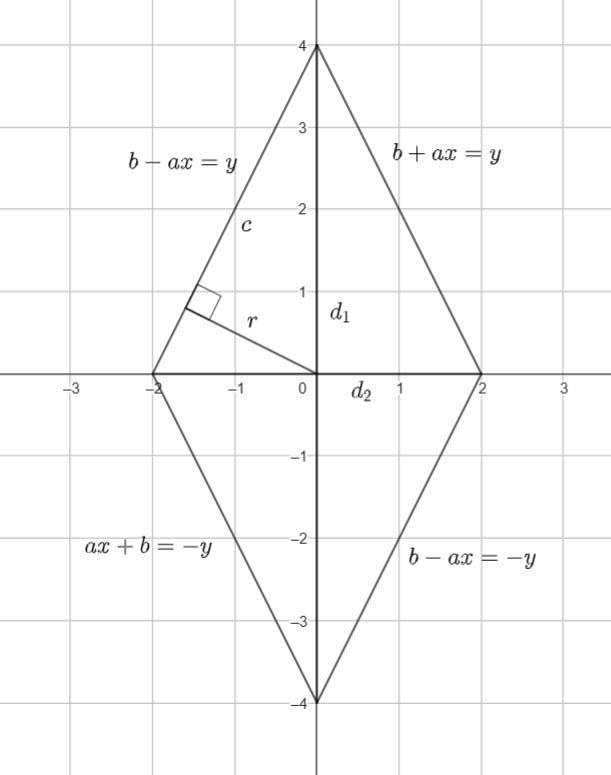
Рассмотрим площадь ромба $S =d1d2∕2.$ Его диагонали имеют длины $d1 =$ $2 2b∕a,d2 = 2b,S = 2b ∕a,$ сторона $∘ 2------2 √ -2--- − c= b +(b∕a) = b a +1∕a.$