Тема backlog (работа над имеющимися решениями)

backlog (работа над имеющимися решениями)

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#127567Максимум баллов за задание: 7

Решите в целых числах $x$ и $y$ уравнение

3 3 2 x = y +2y + 1.

Показать ответ и решение

Решение скрыто

Ответ:

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#132775Максимум баллов за задание: 7

Решите систему уравнений

{ x+ ∘x2-− 25y2 = 50, ∘-2-----2 5y+ x − 25y = 1.

Показать ответ и решение

Решение скрыто

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 3#132776Максимум баллов за задание: 7

Решите систему уравнений

(| x2+ 4y2 { --xy---= 5; |( 2x2− y2 = 31.

Показать ответ и решение

Решение скрыто

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 4#137765Максимум баллов за задание: 7

В прямоугольной таблице $m$ строк и $n$ столбцов $(m < n).$ В некоторых клетках таблицы стоят звездочки, так что в каждом столбце стоит хотя бы одна звёздочка. Докажите, что существует хотя бы одна такая звездочка, что в одной строке с нею находится больше звездочек, чем с нею в одном столбце.

Показать доказательство

Из исходной таблицы со звёздочками построим две новые, в которых звёздочки заменены числами: в первой таблице эти числа в каждом столбце, содержащем $k$ звёздочек, равны $1 k,$ а во второй — числа в каждой строке с $l$ звёздочками равны $1 l.$ Сумма всех чисел в первой таблице равна $n,$ а во второй — $m.$ Поскольку $m < n,$ то существует такое место, на котором число из первой таблицы больше числа из второй, то есть $1 1 k > l.$ Таким образом, число $k$ звёздочек в соответствующем столбце меньше числа $l$ звёздочек в соответствующей строке.

Ошибка.
Попробуйте повторить позже

Задача 5#140751Максимум баллов за задание: 7

В треугольнике $ABC$ проведены высота $BH$ и биссектриса $BL.$ Точки $P$ и $Q$ — основания перпендикуляров, опущенных из $A$ на $BL$ и из $L$ на $BC$ соответственно. Докажите, что точки $H,P$ и $Q$ лежат на одной прямой.

Показать доказательство

Решение скрыто

Ошибка.
Попробуйте повторить позже

Задача 6#140755Максимум баллов за задание: 7

Лемма 255. В треугольнике $ABC$ проведена биссектриса угла $B.$ Перпендикуляр из точки $C,$ опущенный на эту биссектрису, пересекает её в точке $K.$ Докажите, что

(a) точка $K$ лежит на средней линии треугольника $ABC,$ параллельной $AB;$

(b) точка $K$ лежит на прямой, соединяющей точки касания вписанной окружности со сторонами $AB$ и $AC.$

Показать доказательство

Решение скрыто

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#140758Максимум баллов за задание: 7

Даны четыре попарно пересекающиеся прямые. Докажите, что проекции их точки Микеля на эти прямые лежат на одной прямой.

Показать доказательство

Решение скрыто

Ошибка.
Попробуйте повторить позже

Задача 8#141356Максимум баллов за задание: 7

Решите уравнение

x2+6- -x--- 1 x + x2 +6 =55

Показать ответ и решение

Решение скрыто

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 9#141357Максимум баллов за задание: 7

Решите уравнение

(x+ 1)(x+ 3)(x+ 5)(x+ 7) =945

Показать ответ и решение

Решение скрыто

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 10#141358Максимум баллов за задание: 7

Решите уравнение

2 2 1- x +2x+ x + x2 = 1

Показать ответ и решение

Решение скрыто

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 11#141362Максимум баллов за задание: 7

Решите уравнение

2 -9x2-- x + (x+ 3)2 = 16

Показать ответ и решение

Решение скрыто

Ответ:

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#83155Максимум баллов за задание: 7

Докажите, что по любому простому модулю $p$ существует первообразный корень.

Показать доказательство

Ключевая лемма. Докажите, что если показатели каких-то двух чисел $a$ и $b$ равны $d$ и $k$ соответственно такие, что $(d,k)= 1,$ то существует число, показатель которого равен $ordpab= dk.$

Доказательство. Во-первых, $dk dk kd (ab) ≡(a )(b) ≡ 1 (mod p).$ Осталось понять почему эта степень минимальная. Пусть $ordpab= t.$ Тогда $t (ab) ≡ 1 (mod p).$

Возведем в степень $k.$

(ab)kt ≡akt(bk)t ≡akt ≡ 1 (mod p)

то есть $kt..orda =d . p$ и $t..d, .$ так как $(d,k)= 1.$ Аналогично $t..k, .$ то есть $t..dk, .$ значит, $t= dk.$

______________________________________________________________________________________________________________________________________________________

Теперь вернемся к доказательству теоремы. Пусть $d1,...,dp−1$ — показатели чисел $1,...,p− 1$ соответственно.

НОК( $d1,...,dp− 1$ ) = $α1 αn q1 ⋅...⋅qn .$ Тогда есть $.. α1 di.q1 .$ Если у $a$ показатель $dk,$ то хочется сказать, что у числа $d a$ показатель $k,$ ведь $dk .. a − 1 .p$ и, если существует $k1 <k$ такой, что $dk1 .. a − 1.p,$ то у $a$ показатель был бы меньше.

Раз $.. α1 di.q1 ,$ то $α1 di = q1 ⋅X.$ Значит, существует число $X (i ),$ у которого показатель $α1 q1 .$ Тогда найдем такие числа для каждого простого $qj$ и перемножим их. По предыдущей лемме у произведения показатель будет НОК( $d1,...,dp−1).$

Осталось доказать, что $H$ = НОК( $d1,...,dp−1$ ) = $p − 1.$ $.. p− 1.di =ordpi$ по свойству показателя. Значит, $.. p− 1 .H$ и $p− 1≥ H.$

Давайте рассмотрим сравнение $xH ≡ 1 (mod p).$ С одной стороны, корней не больше, чем $H.$ С другой стороны, $. H..di$ для любого $i,$ поэтому $iH ≡ 1 (mod p),$ то есть решений хотя бы $p− 1$ и $H ≥ p− 1.$ Соединяем $2$ последних факта и получаем, что $H = p− 1,$ то есть мы найдем первообразный корень.

Ошибка.
Попробуйте повторить позже

Задача 13#122737Максимум баллов за задание: 7

(a) Основное свойство поляры. Покажите, что точка $A$ лежит на поляре точки $B$ тогда и только тогда, когда $B$ лежит на поляре точки $A.$

(b) Поляры точек $A$ и $B$ пересекаются в точке $C.$ Чем является поляра точки $C?$

Показать доказательство

Решение скрыто

Ошибка.
Попробуйте повторить позже

Задача 14#122746Максимум баллов за задание: 7

Через произвольную точку $X$ провели секущую к окружности $ω$ . Она пересекла окружность в точках $A$ и $B.$ Докажите, что точка пересечения касательных к $ω$ в точках $A$ и $B$ лежит на поляре $X.$

Показать доказательство

Ошибка.
Попробуйте повторить позже

Задача 15#122747Максимум баллов за задание: 7

Докажите, что точка $A$ лежит на поляре точки $B$ относительно окружности с центром $O$ и радиусом $R$ тогда и только тогда, когда $------ 2 (OA,OB )=R .$

Показать доказательство

Решение скрыто

Ошибка.
Попробуйте повторить позже

Задача 16#122748Максимум баллов за задание: 7

Докажите, что точки $A,B$ и $C$ лежат на одной прямой тогда и только тогда, когда их поляры $a,b$ и $c$ пересекаются в одной точке.

Показать доказательство

Решение скрыто

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#122749Максимум баллов за задание: 7

(a) Пусть точка $Y$ лежит на поляре к точке $X$ относительно окружности $ω.$ Пусть прямая $XY$ пересекает $ω$ в точках $A$ и $B.$ Докажите, что $(X, Y,A,B )=− 1.$

(b) Полярное свойство секущих. Через точку $X$ провели две прямые, которые пересекли окружность $ω$ в точках $A,B$ и $C,$ $D$ соответственно. Тогда точка пересечения $AC$ и $BD$ и точка пересечения $AD$ и $BC$ лежат на поляре точки $X.$

Показать доказательство

Решение скрыто

Ошибка.
Попробуйте повторить позже

Задача 18#122753Максимум баллов за задание: 7

Четырёхугольник $ABCD$ вписан в окружность с центром $O$ . Пусть $P = AB ∩CD,$ $Q= AD ∩ BC,$ $R =AC ∩ BD.$

(a) Докажите, что поляры точек $P,Q$ и $R$ есть прямые $QR,PR$ и $PQ$ соответственно.

(b) Докажите, что $O$ является ортоцентром треугольника $PQR.$

Показать доказательство

Ошибка.
Попробуйте повторить позже

Задача 19#122755Максимум баллов за задание: 7

Пусть в четырёхугольник $ABCD$ вписана окружность $ω,$ которая касается сторон $AB, BC,CD$ и $DA$ в точках $K,L,M$ и $N$ соответственно. Прямые $KL$ и $MN$ пересекаются в точке $S,$ а прямые $LM$ и $NK$ — в точке $T.$ Прямые $AB$ и $CD$ пересекаются в точке $P,$ $BC$ и $AD$ — в точке $Q.$ Докажите, что тогда

(a) $P,Q,S$ и $T$ лежат на одной прямой;

(b) прямые $AC,BD, KM$ и $LN$ пересекаются в одной точке.

Показать ответ и решение

Решение скрыто

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 20#122939Максимум баллов за задание: 7

Теорема Кэзи, слабая версия. Предположим, что на плоскости даны окружность $ω$ и три точки $A$ , $B$ , $C$ вне неё, не лежащие на одной прямой. Обозначим длины отрезков касательных из точек $A$ , $B$ , $C$ к окружности $ω$ через $ta$ , $tb$ , $tc$ соответственно. Тогда окружность $(ABC )$ касается окружности $ω$ в том и в только в том случае, если для некоторой расстановки знаков « $+$ » и « $−$ » выполнено соотношение

±ta ⋅BC ± tb⋅CA ± tc⋅AB = 0.

Показать доказательство

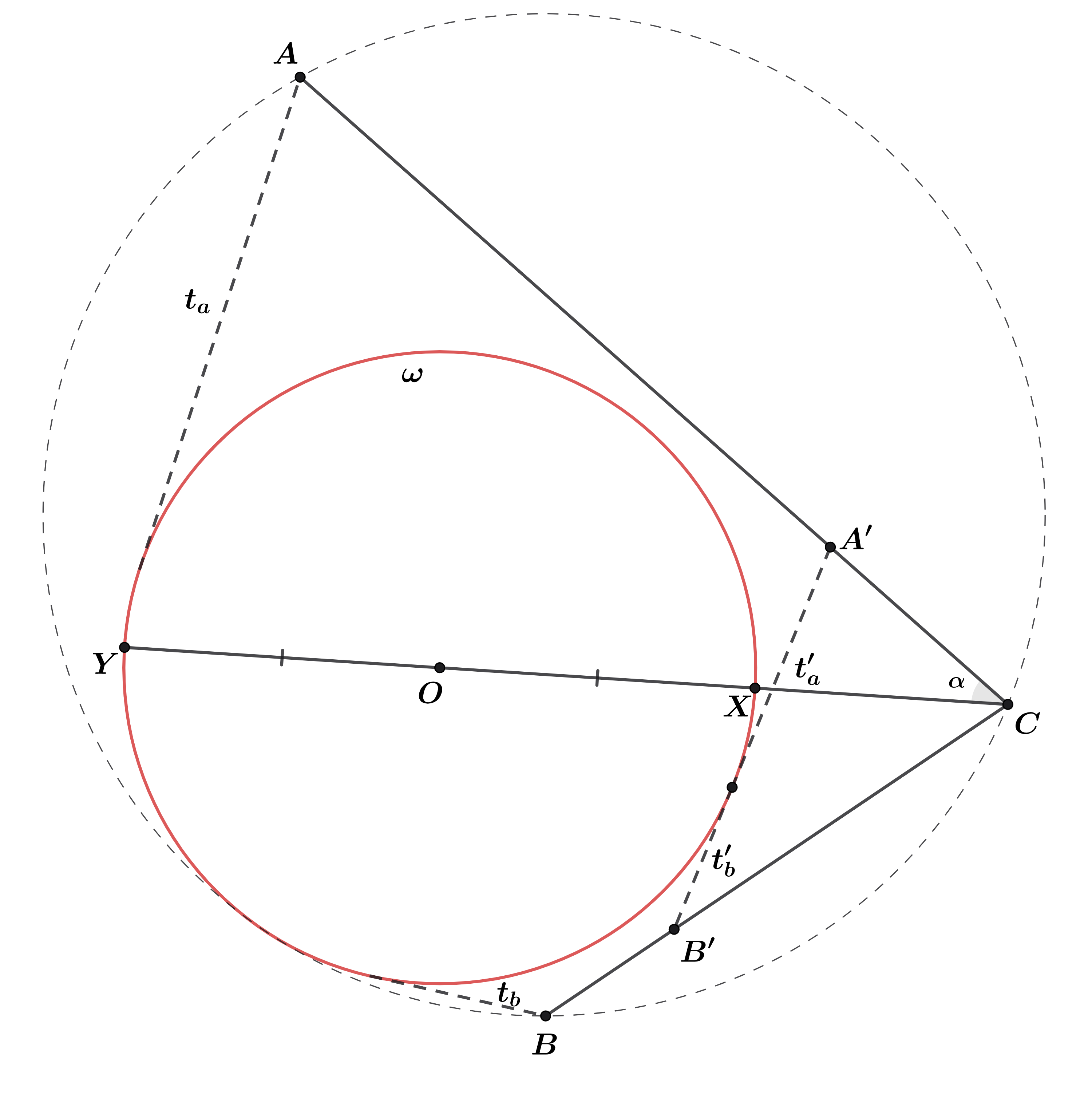
В одну из сторон это утверждение просто частный случай теоремы Кэзи. Поэтому докажем в другую. Пусть дано, что

ta⋅BC + tb⋅AC = tc ⋅AB.

Тогда хотим доказать, что окружность $(ABC )$ касается окружности $ω.$ Сделаем инверсию с центром в точке $C,$ которая оставляет окружность $ω$ на месте, то есть с радиусом $tc.$ Обозначим образы точек $A$ и $B$ при этой инверсии за $A′$ и $B ′.$ Длины касательных из точек $A′$ и $B′$ до $ω$ равны $t′ a$ и $t′ b$ соответственно. Попробуем выразить $t′ a$ через $ta.$ Пусть $O$ — центр окружности $ω.$ Обозначим за $X$ и $Y$ точки пересечения прямой $OC$ и окружности $ω.$ Пусть $α$ — угол между прямыми $OC$ и $OA.$ Тогда $t2= OA2− r2, a$ где $r$ — радиус окружности $ω.$ Выразим $r$ как $(CY − CX )∕2,$ а $OA2$ посчитаем по теореме косинусов. Отрезок $OC$ выразим как $(CX + CY)∕2.$ Тогда получаем:

2 2 ta = AC + CX ⋅CY − AC ⋅(CX +CY )⋅cosα.

Теперь аналогичным образом посчитаем

′2 ′2 ′ (ta) =A C + CX ⋅CY − AC ⋅(CX + CY )⋅cosα.

Из инверсии знаем, что $CX ⋅CY =AC ⋅AC′ = t2c.$ Поэтому получаем, что:

(t′)2 = t2 ⋅-t2c- a a AC2.

Аналогично

tb =t′b⋅ BC-. tc

Из формулы измения длины отрезка при инверсии знаем, что

AB = A′B′⋅ AC-⋅BC-. t2c

Теперь все подставляем в наше исходное равенство из условия:

′ AC ⋅BC ′ AC ⋅BC ′ ′ AC ⋅BC ta⋅---tc---+ tb⋅---tc---= A B ⋅--tc--.

Сократим на общий множитель и получим $t′a+t′b = A′B′.$ Докажем, что такое возможно только, если прямая $A ′B′$ касается $ω.$ Для этого зафиксируем точку $A′$ и будем искать все такие точки $B ′,$ что верно $t′a+ t′b = A′B′,$ при этом длина отрезка $A′B′$ фиксированная. С одной стороны такие точки лежат на окружности с центром в точке $A′$ и радиусом $A′B′,$ а с другой на окружности концентрической $ω,$ ведь отрезок $t′b$ тоже фиксированной длины. Поэтому таких точек $B′$ не более двух. Но как минимум две такие точки $B′$ легко построить, достаточно пересечь касательные из $A$ к $ω$ и окружность радиуса $A′B′.$ В итоге получаем, что точка $B′$ в любом случае такова, что $A′B′$ касется окружности $ω,$ следовательно после инверсии в $C$ окружность $(ABC )$ касается $ω,$ что и требовалось.

$PIC$