backlog (работа над имеющимися решениями)
Ошибка.
Попробуйте повторить позже
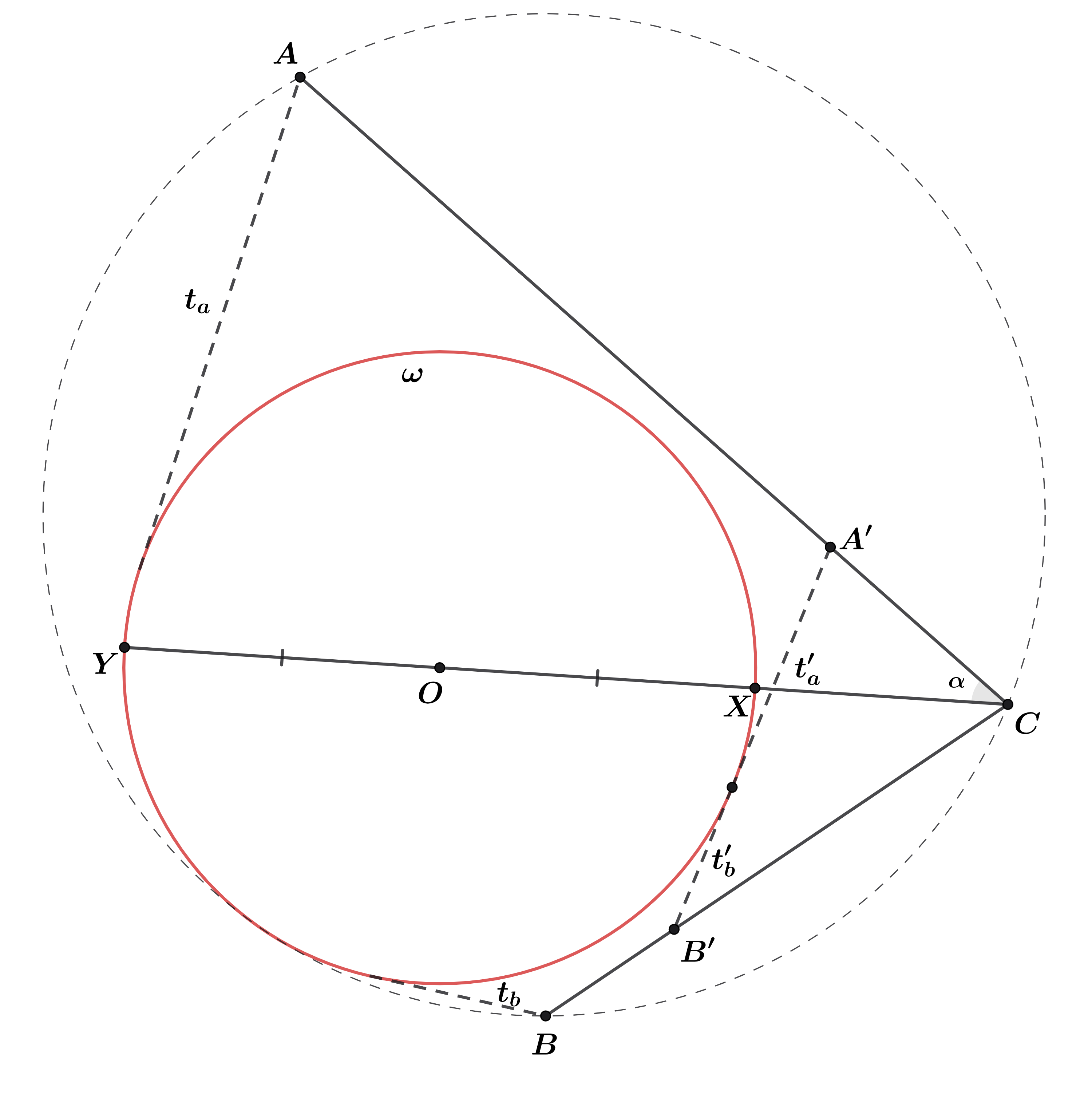
Теорема Кэзи, слабая версия. Предположим, что на плоскости даны окружность и три точки
,
,
вне неё, не лежащие на
одной прямой. Обозначим длины отрезков касательных из точек
,
,
к окружности
через
,
,
соответственно. Тогда
окружность
касается окружности
в том и в только в том случае, если для некоторой расстановки знаков «
» и «
»
выполнено соотношение
В одну из сторон это утверждение просто частный случай теоремы Кэзи. Поэтому докажем в другую. Пусть дано, что
Тогда хотим доказать, что окружность касается окружности
Сделаем инверсию с центром в точке
которая оставляет
окружность
на месте, то есть с радиусом
Обозначим образы точек
и
при этой инверсии за
и
Длины касательных из
точек
и
до
равны
и
соответственно. Попробуем выразить
через
Пусть
— центр окружности
Обозначим
за
и
точки пересечения прямой
и окружности
Пусть
— угол между прямыми
и
Тогда
где
— радиус окружности
Выразим
как
а
посчитаем по теореме косинусов. Отрезок
выразим как
Тогда получаем:
Теперь аналогичным образом посчитаем
Из инверсии знаем, что Поэтому получаем, что:
Аналогично
Из формулы измения длины отрезка при инверсии знаем, что
Теперь все подставляем в наше исходное равенство из условия:
Сократим на общий множитель и получим Докажем, что такое возможно только, если прямая
касается
Для
этого зафиксируем точку
и будем искать все такие точки
что верно
при этом длина отрезка
фиксированная. С одной стороны такие точки лежат на окружности с центром в точке
и радиусом
а с другой на окружности
концентрической
ведь отрезок
тоже фиксированной длины. Поэтому таких точек
не более двух. Но как минимум две такие
точки
легко построить, достаточно пересечь касательные из
к
и окружность радиуса
В итоге получаем, что точка
в
любом случае такова, что
касется окружности
следовательно после инверсии в
окружность
касается
что и
требовалось.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




