.02 Конус Маха
Ошибка.
Попробуйте повторить позже
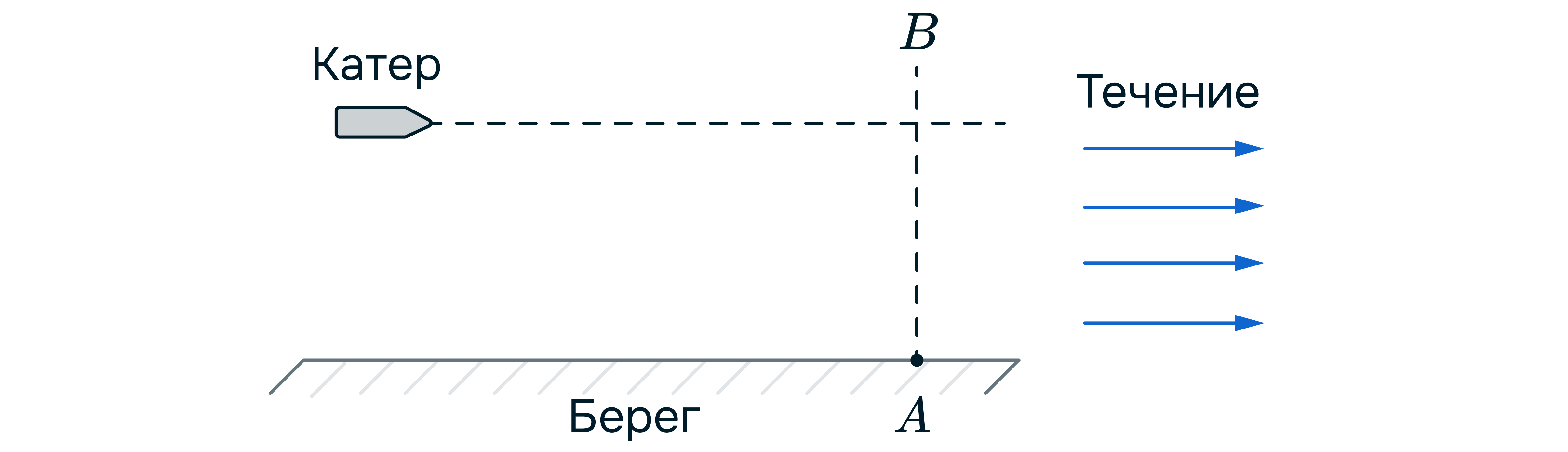
Вдоль направления течения прямой реки по спокойной воде плывёт маленький катер, траектория которого параллельна
берегу и лежит на расстоянии от него. Скорость течения реки равна
Стоящий на берегу в точке
наблюдатель
увидел, что первая волна от катера достигла точки
спустя время
после того, как катер пересёк прямую
перпендикулярную берегу (см. рис.). После этого волны ударяли о берег в этом месте с периодом
Расстояние между
соседними гребнями волн равно
Найдите скорость катера относительно воды, считая, что волны, возбуждаемые
катером на поверхности воды, близки к гармоническим.
Источники:
Пусть – скорость катера относительно стоячей воды,
– скорость распространения волн относительно поверхности
стоячей воды. Запишем формулу для скорости волн, учитывая, что они близки к гармоническим:
где – период волн в системе отсчёта, связанной с водой.
Перейдём в систему отсчёта, связанную с катером:
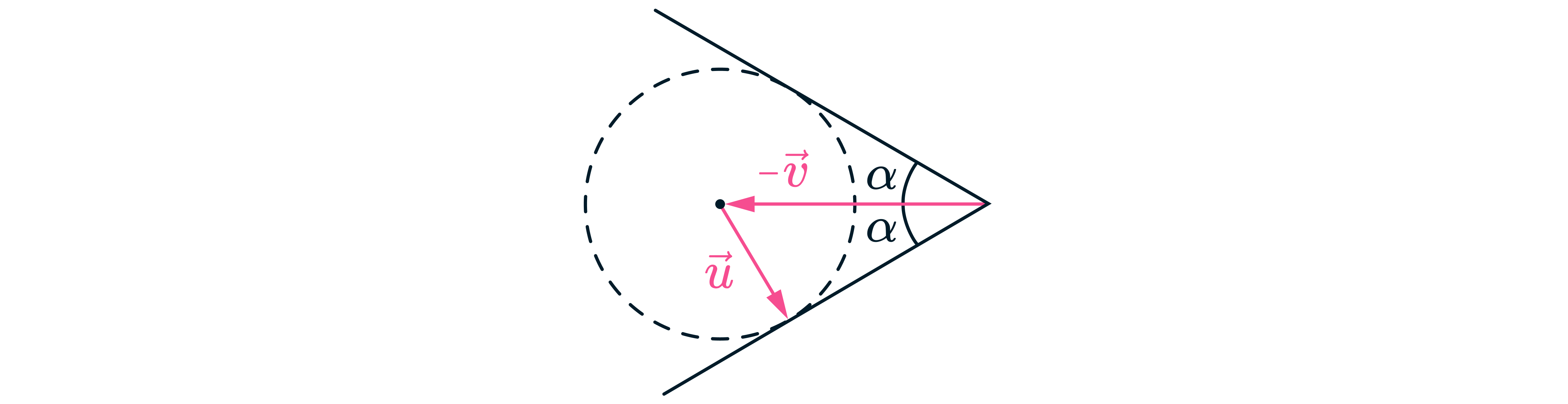
В этой системе отсчета вода движется относительно катера со скоростью - , а волны распространяются относительно
воды из каждой точки, в которой находился катер, во всех направлениях со скоростью, по модулю равной
(иначе говоря, гребни волн, испущенных в некоторый момент, в следующие моменты времени находятся на
одинаковом расстоянии от точки испускания, которая движется со скоростью
). Из закона сложения скоростей
следует, что относительно катера волны распространяются только внутри угла
изображённого на первом
рисунке (это так называемый «конуса Маха»; в трёхмерном случае волны распространяются внутри конуса).
Относительно берега реки «конус Маха» как единое целое движется со скоростью , и поэтому гребни волн
образуют с берегом тот же угол
что изображён на первом рисунке. Из условия задачи следует, что
(иначе волны обгоняли бы катер, и первая волна пришла бы в точку
до того, как катер пересек линию
).
Рассмотрим рисунок, на котором показан гребень волны и набор параллельных ему гребней следующих
волн.
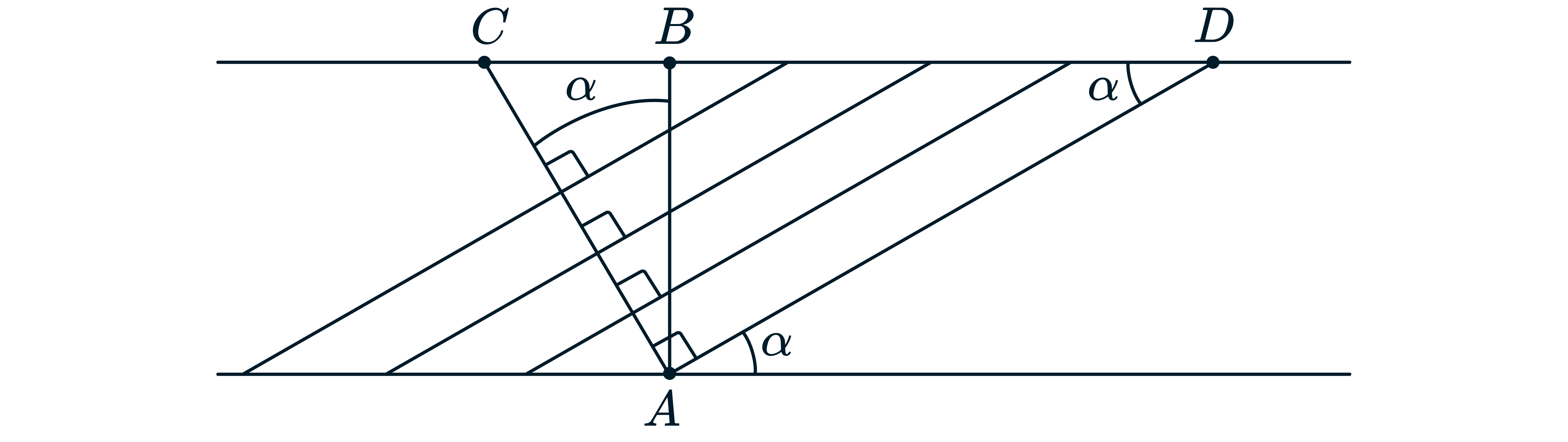
В точку дошла волна, испущенная из точки
а катер за это время прошёл отрезок
Из первого рисунка и
второго рисунка следуют уравнения (1) и (2):
Свяжем величины и (то есть фактически учтем эффект Доплера). Если волны распространяются в стоячей воде, то
скорость движения вдоль берега точки
(это точка пересечения линии гребня волны с берегом) равна
Отрезок
Поэтому
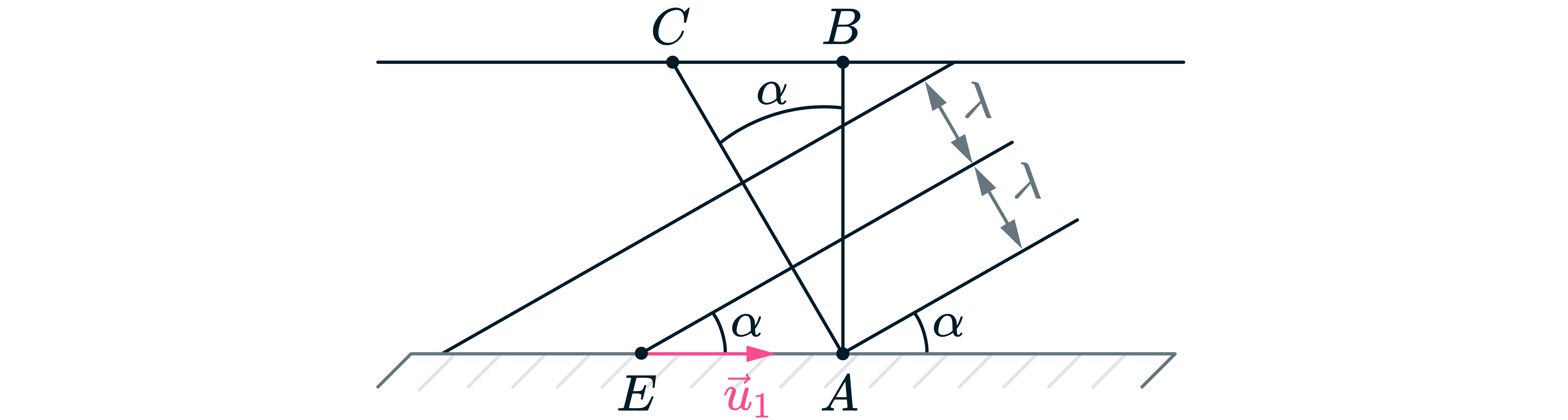
. Если же волны распространяются в воде, которая течет со скоростью
то эту скорость течения нужно добавить к скорости
и учесть, что изменится период волн. При этом получится
следующее соотношение:
где
- заданный в условии задачи период волн, наблюдаемых в системе
отечета, связанной с берегом.
Отсюда
С учетом уравнения (1),
Далее, с учетом уравнения (2):
Отсюда
Окончательно получаем:
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




