.01 Барометрическая формула
Ошибка.
Попробуйте повторить позже
молекул идеального газа находятся при температуре 
в закрытом вертикальном цилиндрическом сосуде в поле силы
тяжести. Высота цилиндра 
, площадь основания 
, масса одной молекулы 
. На вебинары был рассмотрен случай
изотермической модели. Начнем изменять температуру (то есть 
).
1. Как в таком случае выглядит закон изменения концентрации от координаты 
?
2. Как в таком случае будет выглядеть выражение для координаты центра масс газа?
3. Определите удельную потенциальную энергию (то есть потенциальную энергию на одну молекулу).
Проанализируем изменение концентрации у дна сосуда при изменении температуры в двух предельных случаях.
При низких температурах 
и
то есть все молекулы собираются на дне сосуда.
При высоких температурах 
и
![[ ( )]−1 ( mgH )
n(0) ≈ ⟨n⟩a 1− 1− a + a2∕2 − ... ≈ ⟨n⟩(1+ a∕2) = ⟨n⟩ 1 +----- ,
2kBT](/api/latex-service/v1/GetSession/205989/index-fd7e8d215dc869aeb9bced33f632e814.svg)
т.е. плотность молекул на дне приближается к среднему значению.
В случае высоких температур плотность молекул на высоте 
:
![[ mgH--] ( mgz)
n(z;T ≫ mgH ∕kB) ≈ ⟨n ⟩ 1+ 2kBT exp − kBT ≈
[ mgH ][ mgz ]
≈ ⟨n⟩ 1 + ----- 1− ---- .
2kBT kBT](/api/latex-service/v1/GetSession/205989/index-a567150fd974e8a53749680682a8f2a7.svg)
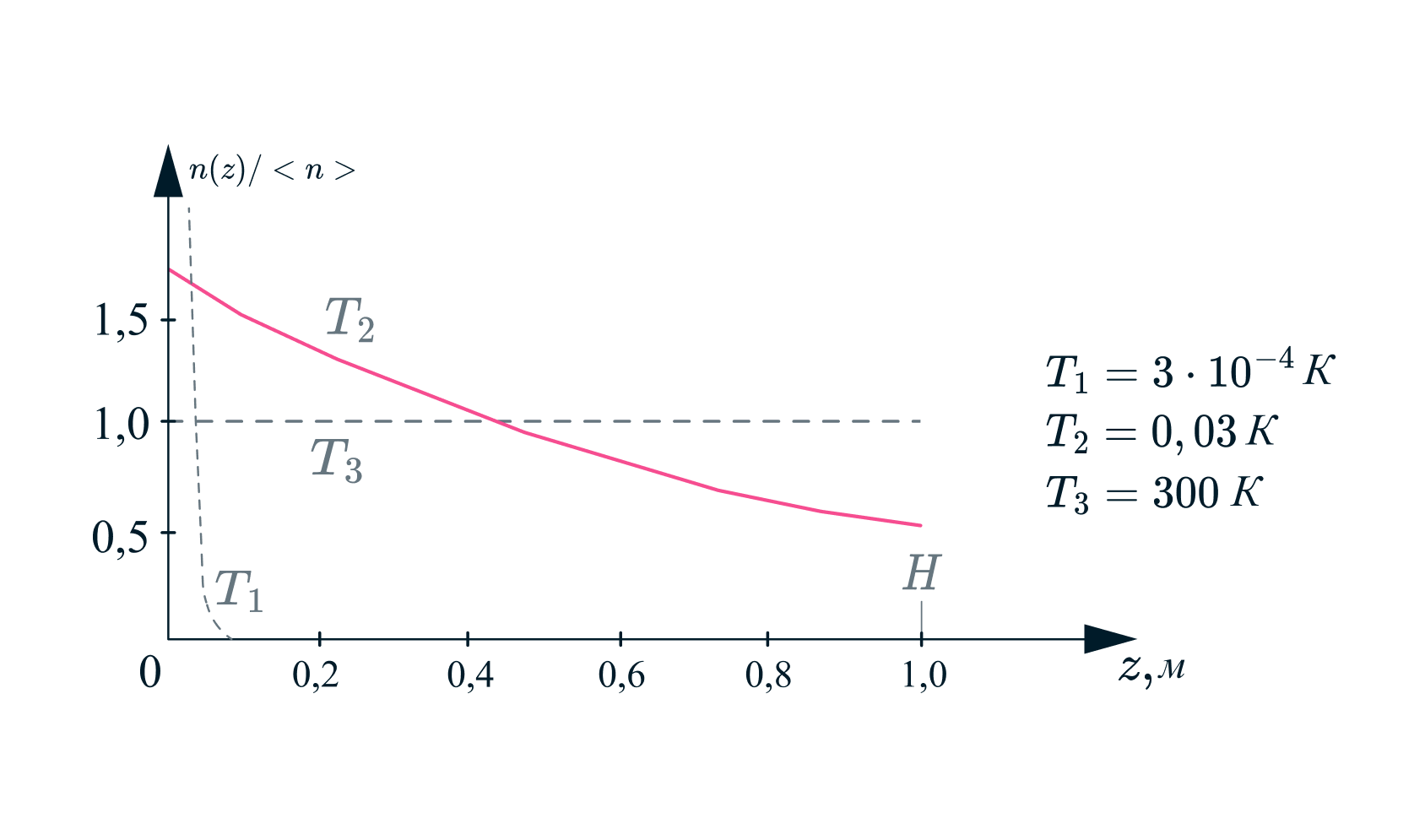
На рис.3.2 представлены зависимости 
для трех температур: 
.
При 
концентрация 
, что соответствует равномерному распределению частиц по высоте. Заметим,
что площадь под кривой 
есть константа, равная 
.
Координата 
центра масс по определению равна
где 
. Учитывая, что 
, и используя выражение для концентрации, для
координаты центра масс получаем:
![-----a----- H- ea-−-(1-+-a)
zc = 1 − exp(− a) ⋅a2[1− (1+ a)exp(− a)] = H ⋅ a (ea − 1) .](/api/latex-service/v1/GetSession/205989/index-4017e30ec34db86686195d1bc6d2e204.svg)
В предельных случаях:
1) низких температур ( 
):
2) высоких температур ( 
):
Средняя потенциальная энергия в расчете на одну молекулу газа связана с координатой центра масс 
соотношением:
Таким образом,
![a exp (MgH-)− [1 + MgH-]
⟨𝜀пот ⟩ = mgH e-−-(1+-a) = kBT-----RT(----)----RT--.
a(ea − 1) exp MgRHT- − 1](/api/latex-service/v1/GetSession/205989/index-265fc9a10d699aa956e579b2f888e83b.svg)
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
