.01 Барометрическая формула
Ошибка.
Попробуйте повторить позже
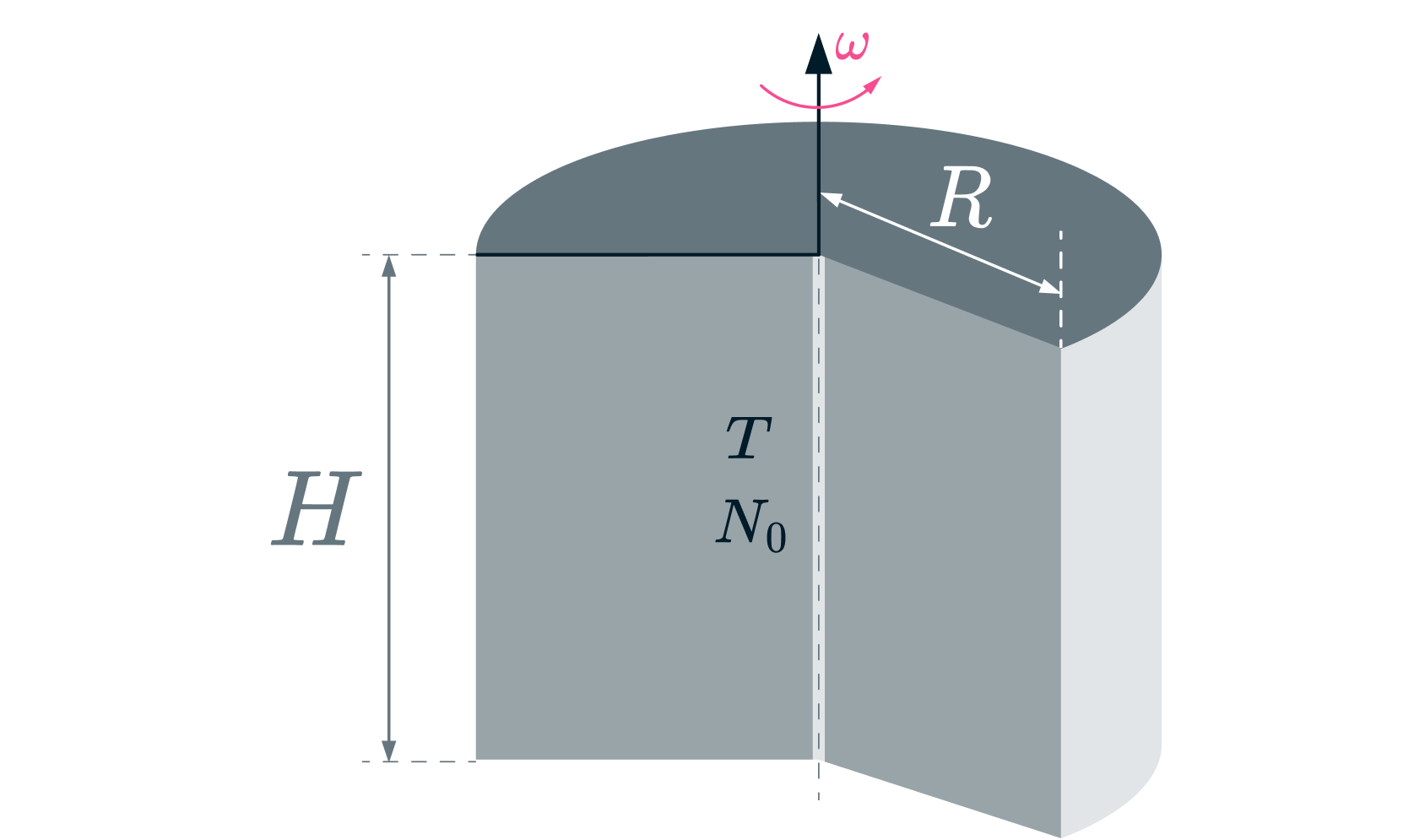
Идеальный газ, имеющий температуру находится в цилиндрическом сосуде, который вращается
вокруг своей оси с угловой скоростью
(см. рис.). Радиус цилиндра
высота
Найти
распределение давления газа вдоль радиуса цилиндрического сосуда, а также давление газа на боковую
стенку цилиндра. Число молекул газа в сосуде
Маса одной молекулы
Силой тяжести
пренебречь.
В неинерциальной системе отсчета, связанной с вращающимся цилиндром, на молекулу идеального газа действует
центробежная сила инерции, величина которой зависит от расстояния молекулы до оси вращения:
Энергия молекулы, находящейся на расстоянии от оси цилиндра, равна (по определению потенциальной энергии)
работе центробежных сил при перемещении молекулы из данной точки
в точку
, где ее потенциальная энергия
равна нулю:
Вероятность обнаружить молекулу в элементарном объеме (тонкий цилиндрический слой с радиусами
и
) определяется распределением Больцмана:
Константу находим из условия нормировки:
где . Число молекул, имеющих координаты в интервале
:
Концентрация молекул на расстоянии от оси вращения:
где средняя концентрация молекул в объеме циллиндра.
Давление на расстоянии от оси вращения (см. рис.):
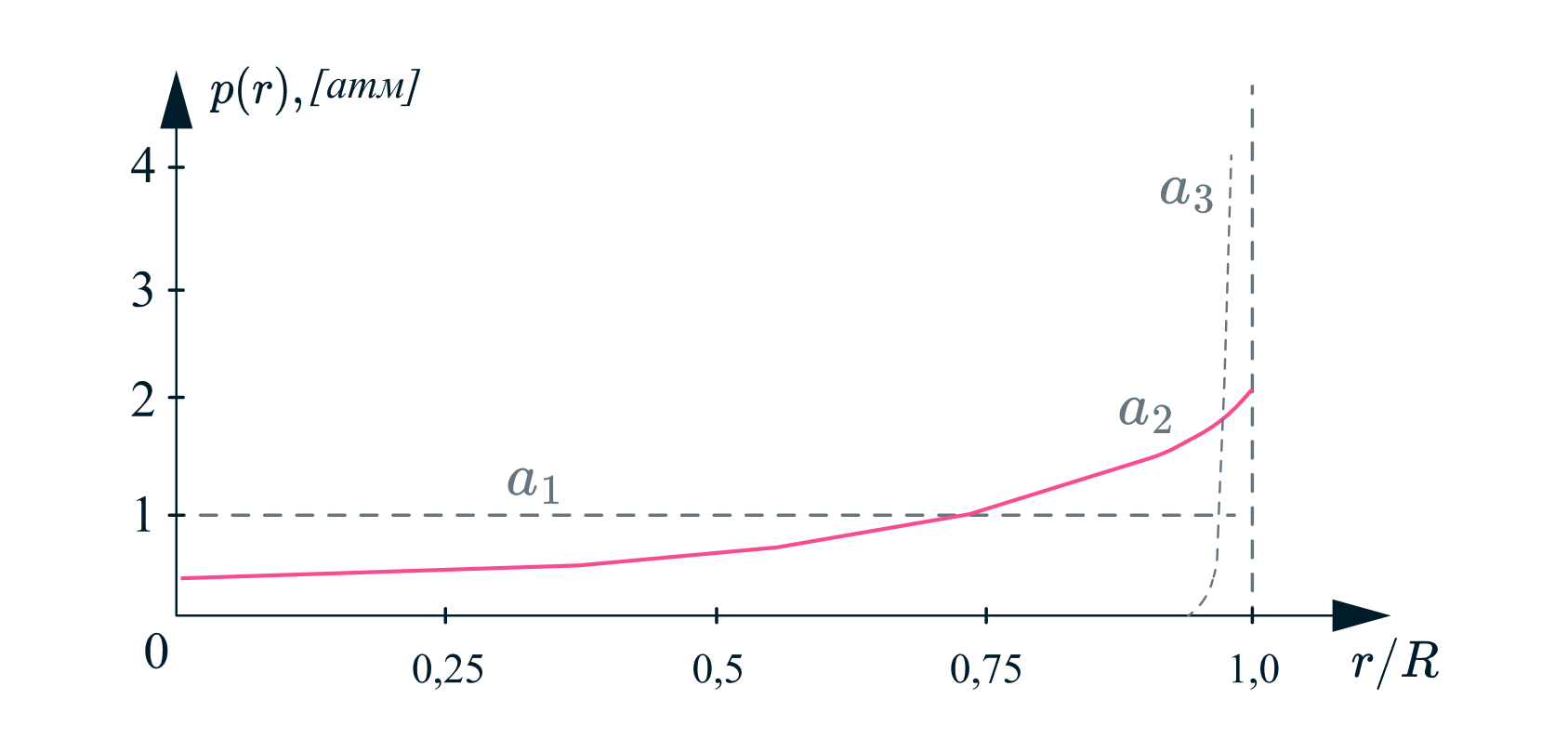
Давление на боковую стенку:
В предельных случаях имеем (см. рис.):
1) При малых скоростях вращения (или при высоких температурах) и можно пренебречь влиянием
центробежных сил:
2) При высоких скоростях вращения (или при низких температурах), т.е. в пределе давление на
боковую стенку сосуда создается всеми молекулами, собирающимися у стенки сосуда:
где - площадь боковой стенки циллиндра.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




