Биссектрисы
Ошибка.
Попробуйте повторить позже
Дан треугольник Пусть
— центр его вписанной окружности,
— такая точка на стороне
что угол
прямой,
— точка, симметричная точке
относительно вершины
Докажите, что точки
лежат на одной
окружности.
Источники:
Подсказка 1
Условие на угол PIB выглядит немного странно...однако он входит в состав угла AIB (I - центр вписанной окружности, так еще нам и намекают число 90) Какой угол тогда хочется сразу посчитать?
Подсказка 2
Угол AIB на 90 больше половины угла ACB, а, значит, углы ACI и AIP равны. На картинке много биссектрис, которые могут помочь нам в поисках подобных треугольников. А еще хочется как-то пользоваться равенством отрезков QA и AI(мы этого еще не делали)
Подсказка 3
Треугольники CIA и IPA подобны по трем углам, а в них как раз присутствует отрезок IA, так что можем записать, что IC/IP = AC/AI = AC/AQ. Смотрим, какие же треугольники содержат отрезки IC, IP, AC, IQ (или хотя бы часть из них, чтобы дальше работать с подобием)?
Подсказка 4
Треугольники ICP и ACQ! Становится ясно: хотим равенства углов CIP и CAQ, чтобы доказать подобие треугольников с такими же названиями, чтобы доказать равенство углов IPC и AQC. Посчитать угол QAC как внешний к половине угла BAC несложно, а угол PIC есть сумма углов AIP и AIC. Осталось лишь воспользоваться знанием про углы с вершиной I из подсказки 2 ;)
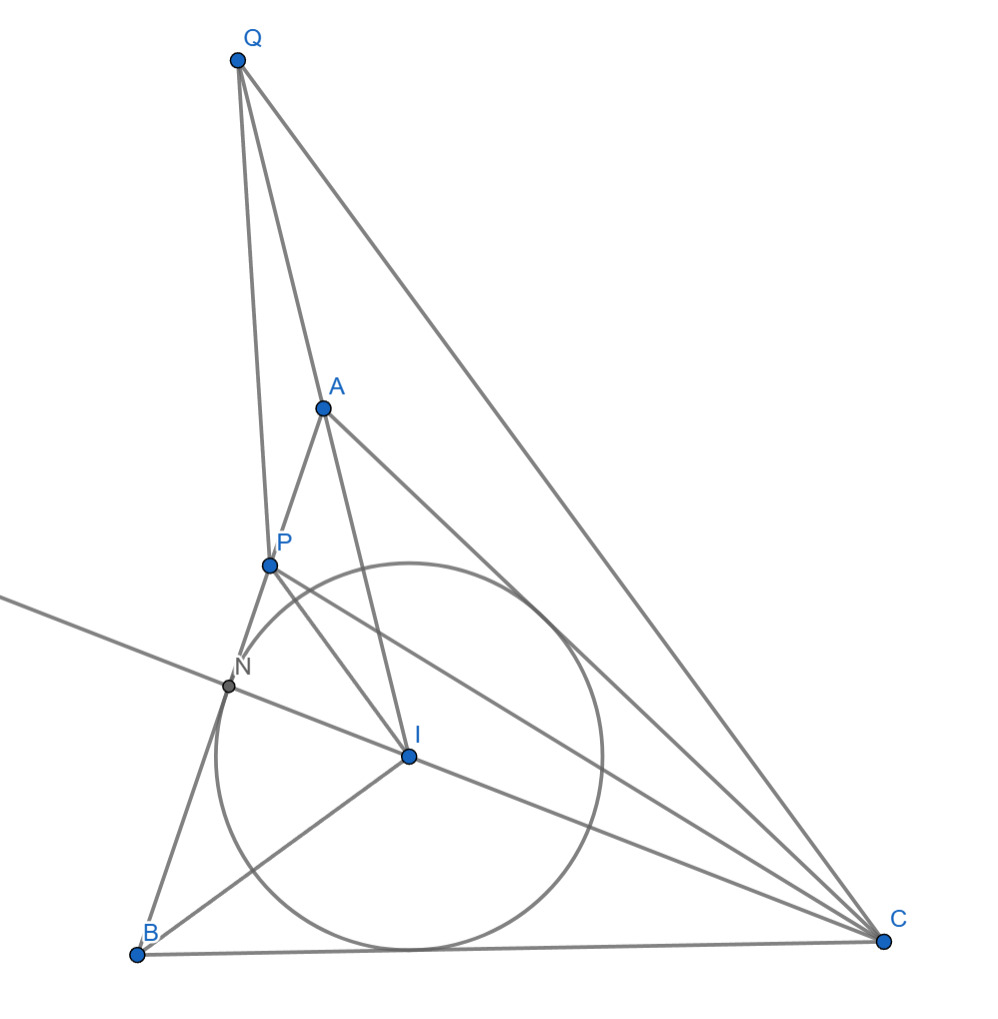
Пусть пересекает
в точке
Угол
тупой, а угол
острый, значит
лежит между
и
Далее, т.к.
— центр
вписанной окружности треугольника, получаем
Значит, треугольники и
подобны. Учитывая это и равенство
имеем
Кроме того,
Следовательно,
Тогда треугольники и
подобны по углу и отношению прилежащих сторон, значит
и точки
лежат на одной окружности.
Замечание. После доказательства подобия треугольников и
можно действовать по-другому. Выберем
точку
на продолжении отрезка
за точку
так, что
тогда треугольники
и
равны
(
). Значит,
— равнобокая трапеция, и она вписана. С другой стороны, поскольку
точки
лежат на одной окружности. Значит, все пять точек
лежат на окружности
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




