Физтех 2023

Чтобы произведение было минимальным, числа не должны иметь простых делителей, отличных от и

Пусть (показатели всех степеней — целые неотрицательные числа). Тогда

Рассмотрим отдельно делимость на и

Из того, что делится на делится на делится на следует, что

Складываем полученные неравенства и получаем:

Покажем, что значение достигается. Для этого возьмём

Из того, что делится на делится на делится на следует, что

Складываем полученные неравенства и получаем:

Покажем, что значение достигается. Для этого возьмём

Из того, что делится на следует, что Заметим, что

может равнятся если, например,

Так как минимум каждой из трёх сумм не зависит от оставшихся, то и минимальное значение равно

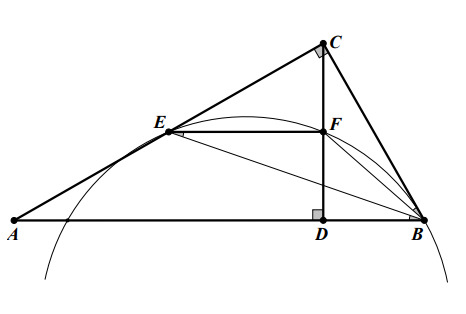
Соединим точку с точками и Так как то а по теореме об угле между касательной и хордой. Поэтому Следовательно, и — соответствующие элементы в подобных прямоугольных треугольниках и (По двум углам: — общий и Значит,

По обобщённой теореме Фалеса

Из полученных равенств следует, что

Значит, — середина а так как то — средняя линия Отсюда

А значит,

Так как по определению

То уравнение равносильно

Второе уравнение системы равносильно совокупности

Эта совокупность задаёт две непересекающиеся окружности и — с центрами в точках и и радиусами и соответственно.

Теперь рассмотрим первое уравнение системы:

Видим, оно определяет прямую с угловым коэффициентом При фиксированном значении — т.е. при фиксированном угле наклона — и при получаем всевозможные прямые с угловым коэффициентом

Чтобы система имела ровно решения, прямая должна пересекать каждую из окружностей ровно в двух точках. Это возможно в том и только том случае, когда угловой коэффициент прямой по модулю меньше, чем угловой коэффициент общей внутренней касательной двух данных окружностей (тогда за счёт выбора параметра можно подобрать такое положение прямой, что она пересекает каждую из окружностей дважды).

Проведём общую внутреннюю касательную к окружностям (пусть и — точки касания этой прямой с и соответственно). Пусть — прямая, параллельная и проходящая через точку пусть также ( поэтому — угол наклона общей внутренней касательной). Так как

а также то из прямоугольного имеем

Значит,

С учётом сказанного выше подходят все значения углового коэффициента, по модулю меньшие, чем откуда

Обозначим , Так как

то исходные уравнения можно записать в виде

Рассмотрим первое уравнение системы. Возьмём производную от левой части, получим

Т.е. в левой части стоит возрастающая функция, а в правой части число, поэтому уравнение имеет не более одного решения. С другой стороны, любой многочлен нечётной степени имеет по крайней мере один действительный корень. Отсюда следует, что уравнение имеет ровно одно решение.

Аналогично рассмотрим второе уравнение:

Значит, аналогично с первым уравнением, второе уравнение имеет ровно одно решение. Если во втором уравнении сделать замену то оно принимает вид

Это эквивалентно первому уравнению. Это означает, что корни уравнений противоположны, следовательно, их сумма равна нулю. Тогда

Запишем исходное условие на координаты точек и в виде

Так как координаты точек и являются целыми числами, то левая и правая части этого равенства могут принимать только целочисленные значения Пара точек и с целочисленными координатами удовлетворяет условию тогда и только тогда, когда они лежат на параллельных прямых

соответственно. Найдём подходящие значения параметра

Стороны и параллелограмма лежат на прямых

поэтому они параллельны прямым, на которых лежат точки и Эти прямые пересекают параллелограмм при

Выясним количество точек с целочисленными координатами на каждой из прямых вида

Рассмотрим несколько вариантов:

Если кратно трём (т.е. то получаем прямую

При любом целом получится целое значение а чтобы точка оказалась в параллелограмме нужно, чтобы

При любом этому неравенству удовлетворяет целых значений

Если не делится на 3, т.е. при где имеем

Учитывая, что получаем

Значит, этому неравенству удовлетворяет целочисленных значений.

Если (таких значений то на каждой из двух прямых

можно выбрать по точек — всего пар.

Если (таких значений то на каждой из двух прямых можно выбрать по точек — имеем пар.

Итого получаем

а)

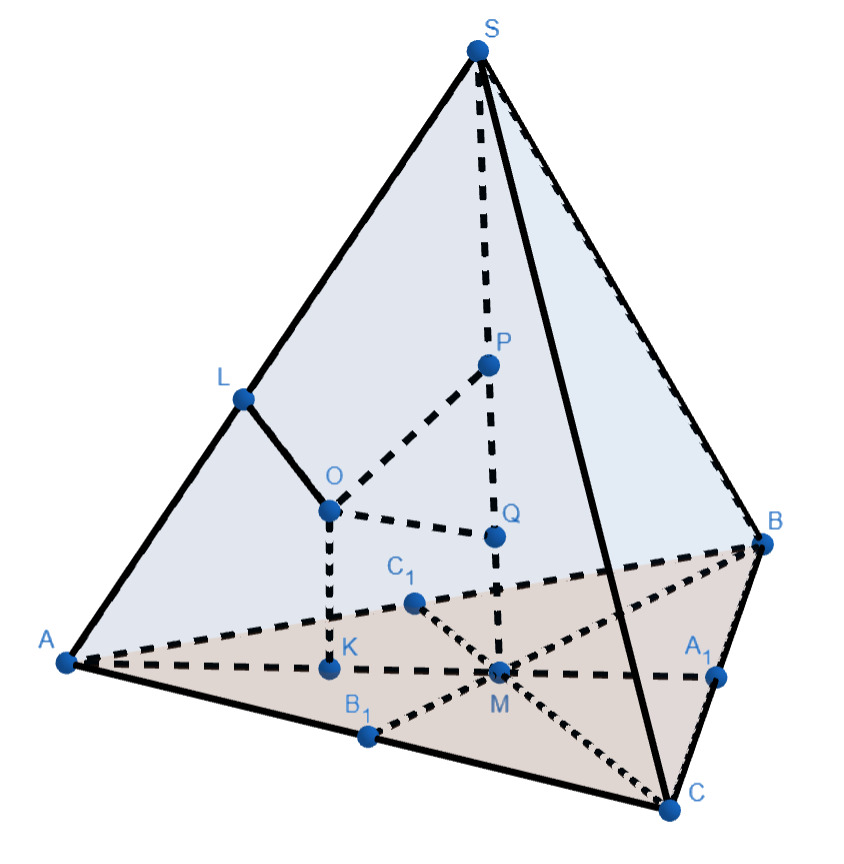
Поскольку — касательная к сфере а и — секущие к ней, то по теореме о касательной и секущей

Аналогично,

А поскольку то

В итоге получаем

Так как как касательные к сфере проведённые из точки то

А поскольку медианы треугольника точкой пересечения делятся в отношении считая от вершины, то

Кроме того,

При этом

то есть

Отсюда прямоугольный и Далее имеем

Значит,

б)

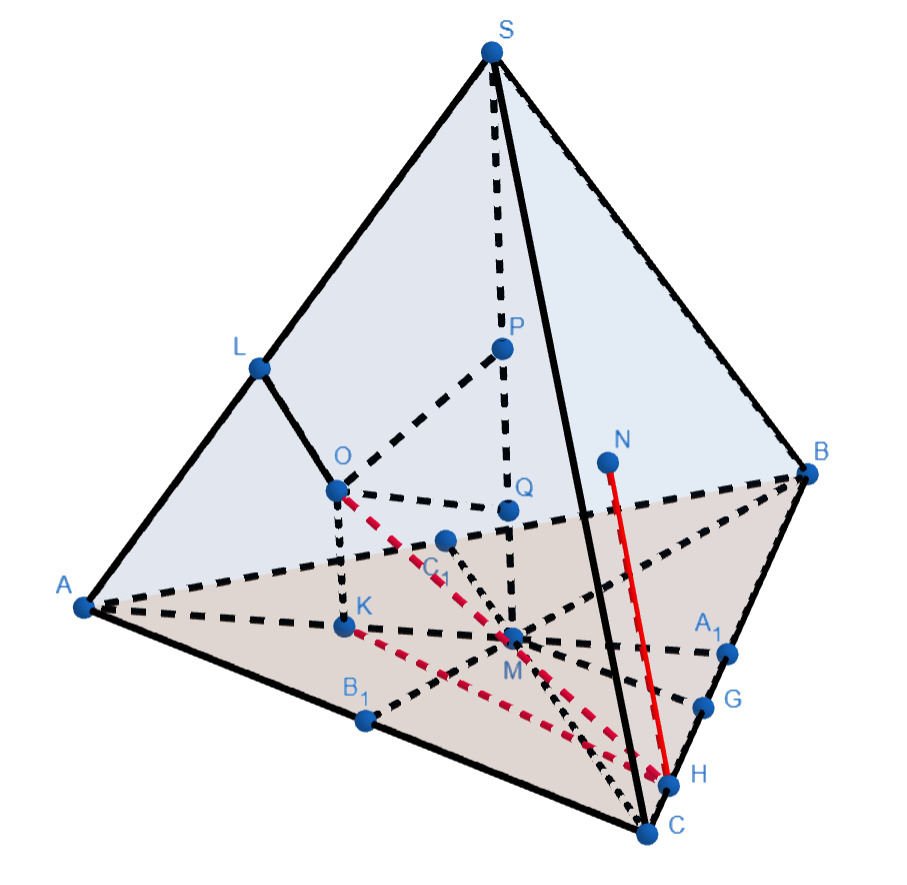
Пусть и — проекции точек и на прямую соответственно. Заметим, что потому что и — точки касания сферы со сторонами двугранного угла пирамиды при ребре Поэтому искомый угол равен

где — центр сферы

Далее имеем

Так как как касательные к то

Отсюда получаем

Из подобия и имеем

Окончательно,

Пусть и — вершины квадрата, лежащие в первой и четвёртой четвертях соответственно; — начало координат.

По условию точка лежит на прямой . Если — абсцисса точки , то , а координаты точки — это . Так как точка получается из поворотом на против часовой стрелки вокруг точки то её координаты . Поскольку обе точки лежат на графике , получаем и решаем систему уравнений (учитываем, что )

Пусть — половина диагонали квадрата. Тогда

Площадь квадрата равна полупроизведению его диагоналей, то есть

Найдём сначала количество троек натуральных чисел. Пусть

где — целые неотрицательные числа. Тогда получаем

Числа составляют в указанном порядке геометрическую прогрессию тогда и только тогда, когда , откуда

Из полученных уравнений получаем систему

Посчитаем количество решений этой системы. Есть способ выбрать пару чисел . Действительно, можно взять любым целым числом из отрезка , после чего определяется однозначно. Аналогично, пару можно выбрать способом. Перемножая, получаем способ.

Если рассматривать также отрицательные значения переменных, то можно заметить, что подходят все тройки чисел вида , где положительны и составляют геометрическую прогрессию. Таких троек ровно столько, сколько и в первом случае, поэтому окончательно имеем тройки.