Тема Росатом - задания по годам

Росатом 2024

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела росатом - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#83296

На стадионе имеются две беговые дорожки. Каждая из них является границей квадрата со сторонами $200$ м и $300$ м соответственно. Квадраты имеют общую вершину А и две стороны меньшего квадрата лежат на сторонах большего квадрата. Два друга Петя и Коля решили пробежаться, но выбрали для этого разные дорожки. Стартовали одновременно из точки А и бежали $3$ часа в одном направлении с одинаковой скоростью $100$ м/мин. Сколько минут за время тренировки ребята бежали рядом с друг другом?

Подсказки к задаче

Подсказка 1

Назовём общую вершину А, а вершины малого квадрата, лежащие на сторонах большого - B и C. Пусть движение происходит от В к С. Тогда моменты встречи в В определяют начало промежутка в 4 минуты, когда ребята бегут вместе. Как бы найти эти моменты времени для каждого мальчика...

Подсказка 2

Верно, нужно рассчитать, сколько времени потребуется каждому, чтобы добраться до точки В, а затем найти, за сколько минут они пробегут целый круг и вернутся в В. Если мы умножим время, за которое каждый из мальчиков пробегает квадрат на какое-то целое число, и добавим соответствующее время добегания до точки В, то сможем найти все моменты времени, в которые ребята оказывались в этой точке.

Подсказка 3

Получаем 1+3t=2k. Обратите внимание на чётность)

Подсказка 4

Верно, t может быть только нечётным. Иначе говоря, t=2m-1 при нечётном m. Надо только подставить m в начальное уравнение времени касательно t и найти, при скольких m оно меньше 1000. Это и будет количество 4-минутных встреч. И не забудьте прибавить 2 минуты, что ребята вместе пробежали в самом начале!

Показать ответ и решение

Пусть движение происходит в направлении против часовой стрелки. Введём обозначения как показано на рисунке:

$PIC$

Петя бежит по большой дорожке из точки $A$ , Коля — по малой. Моменты времени, в которые Петя и Коля попадают в точку $B$ за $100$ минут бега, описываются сериями: $10+12t,6+ 8k$ (считаем в минутах, $t$ и $k$ — целые). Моменты встречи друзей в точке $B$ определяют начало промежутка времени в $4$ минуты, в течении которого они бегут вместе. Также необходимо учесть, что в самом начале они вместе пробегают отрезок $AC$ за $2$ минуты.

Найдём, когда серии пересекаются: $10 +12t= 6+8k,1+3t= 2k$ . Видим, что если $t$ чётно, то не найдётся такого $k$ , чтобы равенство выполнилось, а если нечётно — найдётся. Значит, $t= 2m − 1$ и серия, описывающая встречи в точке $B,$ имеет вид: $24m − 2$ . За 3 часа встречи происходили при $24m − 2 ≤180 =⇒ m≤ 7$ Значит, они пробегают вместе $2+7⋅4 =30$ минут.

Ответ: 30

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#83297

Пары чисел $(x;y)$ связаны соотношениями

----sin2x----- -----cosy----- ------1------ 1+cosy− sin2x = 1+ sin2x− cosy = sin2x+ cosy− 1.

Найти наибольшее возможное значение величины $cos22x+ sin2y$ .

Источники: Росатом-2024, московский вариант, 11.2 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Когда видишь выражение с тригонометрией и дробями, то становится страшно. Но от одного из этого точно можно избавиться и записать систему из трёх уравнений.

Подсказка 2

Уравнения всё ещё не выглядят красиво, но может, тогда их получится разложить на множители?

Подсказка 3

В знаменателях первой и второй дроби есть одинаковое выражение в виде разности некоторого синуса и некоторого косинуса. После домножения на знаменатель это разность может стать одним из множителей. А ещё совсем нетрудно раскладывается на множители выражение получаемое из равенства первой и третей дробей (вспомните про разность квадратов).

Подсказка 4

Тогда получается 4 случая. 3 из них нетрудные. Но случай, когда в обоих выражениях sin2x + cosy + 1 = 0, не так прост. Искомое выражение удобно было бы свести к виду "число = квадрат какого-то выражения", так как это даёт нам хорошую оценку из-за неотрицательности квадрата.

Показать ответ и решение

Преобразуем равенство первого и второго выражений (домножим на знаменатели, приведём подобные и разложим на множители):

(sin2x− cosy)(sin2x +cosy+1)= 0

Аналогично сделаем с равенством первого и третьего выражений:

(sin2x− 1)(sin2x+ cosy +1)= 0

Рассмотрим $4$ случая:

$1)sin 2x =cosy$ и $sin2x= 1$ . В этом случае $cos22x +sin2y =0$ .

$2)sin 2x =cosy$ и $sin2x+ cosy +1= 0$ , тогда $sin2x= cosy = − 1 2$ и $cos22x +sin2y = 3 2$ .

$3)sin 2x +cosy+1 =0$ и $sin2x= 1$ . Тогда $cosy =− 2$ , что невозможно.

$4)sin 2x +cosy+1 =0$ . Запишем $cos22x+ sin2y$ как $2− sin22x− cos2y$ . Теперь вместо $sin2x$ подставим $− 1− cosy$ и преобразуем: $1− 2cosy− 2cos2y = 3− 1(1+2 cosy)2 2 2$ . Видно, что максимум равен $3 2$ и он достигается при $cosy =− 1 2$ . Осталось заметить, что $cosy = sin2x= − 1 2$ не зануляют знаменатели в изначальных равенствах.

Ответ:

$3 2$

Ошибка.
Попробуйте повторить позже

Задача 3#83298

Найти сумму максимальных нечетных делителей каждого из целых чисел на отрезке $[61;120]$ .

Источники: Росатом - 2024, московский вариант, 11.3 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Интересно, что чисел от 61 до 120 ровно столько же, сколько нечётных от 1 до 120.

Подсказка 2

Чем нечётные отличаются от чётных? Наличием степени двойки. Тогда как удобно представить все числа?

Подсказка 3

Из первого замечания про количество нечётных хочется посмотреть, а сколько чисел вида n * 2ᴷ для каждого нечётного n (меньшего 120) лежит в промежутке от 61 до 120.

Подсказка 4

Оказывается, для каждого такого n одно своё n * 2ᴷ в промежутке от 61 до 120. Попробуйте понять, почему это так, и досчитать искомую сумму нечётных n!

Показать ответ и решение

Для каждого нечетного числа $n$ в промежутке 1 до 119 рассмотрим числа вида $n⋅2k$ , где $k∈ ℕ∪ {0}.$ Докажем, что для каждого $n$ найдётся ровно одно число вида $k n⋅2$ на промежутке от 61 до 120.

Пусть на нашем промежутке не нашлось нужного числа. Тогда должна найтись такая пара чисел $k k+1 (n⋅2 ;n ⋅2 )$ , что

k k+1 n⋅2 ≤ 60, n⋅2 ≥121,

что невозможно, поскольку из первого следует, что

k+1 n ⋅2 ≤ 120

Тогда из нашего утверждения следует, что для любого нечётного числа $n$ , меньшего 120, найдётся число от 61 до 120, что его наибольшим нечетным делителем будет $n$ . Причём для каждого $n$ такое число уникально. При этом нечётных чисел от 1 до 120 ровно 60, как и чисел от 61 до 120. Получается, что искомая сумма равна сумме всех нечётных чисел от 1 до 120.

1+-119- 1+3+ ...+ 119= 2 ⋅60= 3600

Ответ: 3600

Ошибка.
Попробуйте повторить позже

Задача 4#83299

На плоскости нарисовано 300 прямоугольников с вершиной в начале координат, с противоположной вершиной - на гиперболе $y = 3x+5 x$ в точках с абсциссой $x= n,n= 1,2,3,...,300$ , со сторонами параллельными координатным осям. Область $D$ содержит те точки плоскости, которые принадлежат только одному из прямоугольников. Найти площадь $D$ .

Источники: Росатом - 2024, московский вариант, 11.4 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

По своей сути задача геометрическая, а самая важная часть геометрической задачи – рисунок. Постройте график функции f(x) = 3 + 5/x и обозначенные прямоугольники. А теперь посмотрите, что за площади нас просят найти.

Подсказка 2

Каждый прямоугольник будет иметь вверху прямоугольную часть, которая принадлежит только ему. Как можно вычислить её площадь?

Подсказка 3

Как произведение сторон прямоугольника! У него одна сторона равна единице, а вторая разности значений функции в соседних натуральных аргументах. Только вот рассмотрите отдельно последний прямоугольник: у него одна из сторон лежит просто на оси абсцисс.

Подсказка 4

Остаётся только записать и вычислить сумму всех площадей. Поверьте, она удобно сворачивается!

Показать ответ и решение

Обозначим $3+ 5 x$ через $f(x)$ .

У каждого прямоугольника от первого до трёхсотого есть область, содержащаяся только в нём. Эта область является прямоугольником с шириной 1 и высотой $f(n)− f(n +1)$ (если считать $f(301)= 0$ , ведь у последнего прямоугольника нижнее основание лежит уже на оси абсцисс)

Поэтому сумма площадей таких областей равна

f(1)− f(2)+f(2)− f(3)+...+ f(299)− f(300)+f(300)− 0= f(1)= 8

Ответ: 8

Ошибка.
Попробуйте повторить позже

Задача 5#83300

Найти коэффициент $a 49$ многочлена $P(x)= (1+x15+ x17)6$ , если бы он был приведен в форму суммы одночленов вида $k akx ,k = 0,2,3,...,102$ .

Источники: Росатом - 2024, московский вариант, 11.5, по мотивам 10.2 ММО - 2005 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Обратим внимание на степени переменных. Понятно, что при раскрытии скобок для каждого одночлена степень будет вида 17n+15m. Тогда найдём натуральные решения для 17n+15m=49

Подсказка 2

Правильно, единственное решение - (2;1). То есть при перемножении скобок мы 2 раза взяли х¹⁷ и 1 раз х¹⁵. Обратим внимание также, что в заданной скобке перед каждым одночленом коэффициент 1. Как тогда мы можем выразить коэффициент перед х⁴⁹?

Подсказка 3

Конечно, коэффициент перед х⁴⁹ равен количеству способов выбрать комбинацию из двух х¹⁷ и одного х¹⁵ в 6 скобках. Остаётся только это досчитать

Показать ответ и решение

Понимаем, что при раскрытии скобок степень каждого одночлена будет иметь вид $17n +15m,$ где $n$ — количество взятых $x17,m$ — количество взятых $15 x .$ Поэтому решим сначала уравнение в натуральных числах

17n +15m = 49

Нетрудно заметить решение $n= 2,m =1,$ а также что это решение единственное, т.к. иначе, чтобы сохранить нужные остатки, $x$ будет изменяться на кратное 15 число, а $y$ на кратное 17, поэтому одно из них станет отрицательным.

Осталось лишь посчитать количество способов выбрать комбинацию из двух $x17$ и одного $x15$ в 6 скобках:

2 1 6⋅5 C6 ⋅C 4 = 2 ⋅4= 60

Ответ: 60

Ошибка.
Попробуйте повторить позже

Задача 6#83301

Точка $O$ — начало трех отрезков $OA,OB$ и $OC$ лежащих в плоскости $P$ и имеющих длины 3,4 и 7 соответственно. На прямой $L$ , проходящей через точку $O$ и перпендикулярной плоскости $P$ , расположена точка $D$ так, что сумма углов, образуемых прямыми $DA, DB$ и $DC$ с прямой $L$ , равна $∘ 180$ . Найти длину отрезка $OD$ .

Источники: Росатом-2024, московский вариант, 11.6 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Треугольники ODA, ODB и ODC прямоугольные, также они имеют общую сторону OD. Если её обозначить за переменную, как можно будет записать условие на сумму трёх углов?

Подсказка 2

Пусть OD = x, тогда углы выражаются через арктангенсы. Тогда из условия получаем, что сумма трёх арктангенсов равна π. Что же хочется сделать? Взять от обеих частей тангенс! Но для тангенса суммы двух углов мы формулу знаем, чего не скажешь о суммы трёх. А вот π одиноко стоит с правой стороны, тогда можно сначала перенести одно слагаемое на правую часть и потом уже делать махинации со взятием тангенса.

Подсказка 3

Тогда взяв тангенс от обеих частей (но помните, что нужно будет сделать проверку равносильности такого перехода!) и применив формулу тангенса суммы, получаем совсем простое квадратное уравнение для x.

Показать ответ и решение

Обозначим $OD$ через $x$ .

$PIC$

Из прямоугольных треугольников выражаем углы

∠CDO =arctg 7 ,∠BDO =arctg 4,∠ADO = arctg 3 x x x

По условию нам дано

arctg 7 +arctg 4 + arctg 3= π x x x

Преобразуем

7 4 3 arctgx +arctgx = π− arctg x

Возьмём тангенс от обеих частей (проверку равносильности такого перехода отложим) и применим формулу тангенса суммы

tg(arctg 7x)+ tg(arctg 4x) 3 1−-tg(arctg 7)⋅tg(arctg 4) = tg(π − arctgx) x x

-11x--= − 3 1− 28x2 x

28 11 1− x2 =− 3-

x2 = 28⋅3= 6 14

$x= OD >0,$ поэтому подходит только $x= √6$ .

Теперь вернёмся к уравнению до взятия тангенсов и подставим туда этот корень. Правая часть $∘ -- π− arctg 32$ лежит на отрезке $(0,π).$ Левая тоже, потому что оба арктангенса по определению положительные и меньше $π2.$ То есть они не могут отличаться на кратное $π.$ Так что раз тангенсы получились равны, то и сами углы равны.

Ответ:

$√6$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#83305

У Пети в семье, помимо папы, мамы и бабушки, есть ещё братья и сёстры. Средний возраст папы, мамы и бабушки на 15 лет больше среднего возраста детей и на 10 лет больше среднего возраста всех членов семьи. Сколько в семье детей?

Источники: Росатом - 2024, региональный вариант, 11.1 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Давайте составим уравнение. Так как речь идёт о среднем возрасте, можно обозначить сумму возрастов взрослых за x, детей - за y, а количество детей через n. Теперь можем составить систему уравнений.

Подсказка 2

Пользоваться дробями нам не очень удобно, а так как ни одна из переменных не равна нулю, можем домножить уравнения на знаменатели дробей. Заметим, что одна из сторон обоих уравнений одинакова. Остаётся только приравнять другие стороны и выразить отсюда n

Показать ответ и решение

Обозначим сумму возрастов папы, мамы и бабушки через $x$ , сумму возрастов детей через $y$ , а количество детей через $n$ . Тогда справедливы следующие равенства:

x y x x+ y 3 = 15 + n,3 = n-+3 +10

Преобразуем равенства:

nx= 3y+45n,nx= 3y+ 30(n+ 3)

Видно, что

45n = 30(n+ 3)

n= 6

Ответ: 6

Ошибка.
Попробуйте повторить позже

Задача 8#83306

Решить уравнение

x x 4cosπx =[lg(100 ⋅3 )]− [lg[3]]

Здесь $[a]$ – целая часть числа $a$ – наибольшее целое число, не превосходящее $a$ .

Источники: Росатом - 2024, вариант регионов, 11.2 (по мотивам ММО - 2020, 11.2 второго дня)

Подсказки к задаче

Подсказка 1

Сразу, как мы видим логарифмы, надо записывать ОДЗ. ОДЗ здесь будет x >= 0. Дальше, давайте сделаем тождественные преобразования. У нас выходит, что 4cos(pi * x) - 2 = [lg(3^x)] - [lg[3^x]]. Попробуйте посмотреть чему вообще может равняться правая часть. Как нам оценить 3^x (по сути из этой оценки и вытекает значение правой части)?

Подсказка 2

Для любого x можно найти такое k, что 10^(k + 1) > 3^x >= 10^k, k - целое. При этом эта оценка работает и на [3^x] с тем же k. Значит, правая часть всегда 0. Что теперь остаётся сделать?

Подсказка 3

Верно, решить уравнение 4cos(pi * x) = 2 с учетом ОДЗ. После понятных преобразований, нужно получить две серии решений, каждая из которых зависит от периода, и понять для каких периодов x >= 0.

Показать ответ и решение

Запишем ОДЗ

x x [3 ]≥1 =⇒ 3 ≥ 1 =⇒ x ≥0

Сделаем преобразования:

x x 4cosπx = [lg(100 ⋅3 )]− [lg[3 ]]

4cosπx= 2+ [lg(3x)]− [lg[3x]]

Докажем, что $[lg(3x)]− [lg[3x]]= 0.$ Пусть $[lg(3x)]= k,$ тогда $10k+1 > 3x ≥ 10k.$ Если взять целую часть, то получим $10k+1 > [3x]≥10k.$ То есть "перескочить"через целое невозможно, то есть в действительности $[lg(3x)]− [lg[3x]]= 0.$

Тогда получаем

4cosπx= 2 =⇒ cosπx= 1 2

⌊ ⌊ πx = π+ 2πk | x= 1 +2k ||⌈ 3 ⇐⇒ || 3 πx =− π+ 2πn ⌈ x= − 1+ 2n 3 3

С учетом ОДЗ получаем

⌊ x= 1 +2k, k ∈ℤ, k ≥0, || 3 |⌈ 1 x= − 3 + 2n, n∈ ℤ, n≥ 1

Ответ:

$1 +2k, k ∈ℤ, k≥ 0, 3$ $− 1+ 2n, n∈ ℤ, n≥ 1 3$

Ошибка.
Попробуйте повторить позже

Задача 9#83308

Натуральное число $n ≥2023$ имеет простой делитель $p >2$ и другой делитель $q,$ связанный с $p$ соотношением $(p− 1)(q+ 2)=n − 2$ . Найти наименьшее возможное при этих условиях число $n$ .

Источники: Росатом - 2024, региональный вариант, 11.3 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Давайте раскроем скобки, приведём подобные и посмотрим на выражения слева и справа. Что можно сказать про p и q, исходя из того, что они делители числа n? Ведь слева у нас выражение без свободного коэффициента, зависящее от p и q, а справа n.

Подсказка 2

Верно, можно сказать, что 2p кратно q и q кратно p. Как можно сделать оценки на p и q?

Подсказка 3

Можно сказать, что q = kp. Но тогда 2p кратно kp. Равенства быть не может по условию, остаётся только вариант 2p^2 = n. Отсюда понятно, как искать min n: нужно найти min p при 2p^2 ≥ 2023.

Показать ответ и решение

Раскроем скобки:

(p− 1)(q +2)= n− 2 =⇒ pq− q+ 2p − 2 =n − 2

pq− q+2p= n

Раз $p$ и $q$ — это делители $n,$ то выражение в левой части должно делиться на $p$ и $q.$ Следовательно, получаем

(|{ .. q. p |( 2p ... q

То есть $q = kp,$ тогда $2p ... kp,$ откуда следует, что $k =1$ или $k= 2.$ Но так как $q ⁄= p,$ подходит только $q = 2p.$ Подставим:

2 2p − 2p+ 2p= n

2p2 =n

Осталось перебрать чётные $n,$ которые является удвоенным квадратом простого числа. Перебирая $n ≥2023,$ получаем ответ $2⋅372 = 2738.$

Проверка:

(37− 1)(2 ⋅37+ 2)= 2⋅372− 2

(37− 1)(37+ 1)= 372− 1

Ответ: 2738

Ошибка.
Попробуйте повторить позже

Задача 10#83309

Область $G$ на плоскости, ограниченная двумя параболами $y =− 2x2 +3x$ и $y = x2+ px +q,$ имеет площадь 32. Вертикальная прямая $x =1$ разбивает её на две равновеликие части. Найти $p$ и $q$ .

Источники: Росатом - 2024, региональный вариант, 11.4 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Площади, графики, да тут всё намекает на определённый интеграл, а чтобы его найти надо посмотреть на модуль разности графиков, именно модуль, потому что площадь должна быть не отрицательной!

Подсказка 2

Нам сказано, что прямая x = 1 разбивает график на 2 равновеликие части, а парабола сама по себе фигура довольно симметричная, не можем ли мы что-то сказать про точку x = 1 для параболы?

Подсказка 3

Верно, это абсцисса вершины параболы, а мы умеем находить её через коэффициенты параболы, остаётся только посчитать определённый интеграл и получить условие на q, и задача будет уничтожена!

Показать ответ и решение

Обозначим данные параболы $y(x)= −2x2+3x 1$ и $y (x)= x2+ px+ q, 2$ пусть они пересекаются в точках с абсциссами $x1 < x2.$

Ограниченная ими площадь (над одним графиком и под другим) равна модулю разности площадей под графиками на отрезке $[x1,x2].$ А это по формуле Ньютона-Лейбница считается как

||∫ x2 ∫ x2 || ||∫ x2( 2 ) || || x1 y1(x)dx− x1 y2(x)dx||= ||x1 3x + (p − 3)x+ qdx||

Заметим, что полученный интеграл равен площади под графиком параболы $3x2+(p− 3)x+ q$ на отрезке $[x1,x2]$ . По условию прямая $x =1$ делит эту площадь на две равновеликие. Значит, $x= 1$ — абсцисса вершины этой параболы. С одной стороны, она равна $3−6p,$ а с другой стороны, $x1+2x2= 1.$ Тогда находим

3−-p =1 =⇒ p= −3 6

Теперь запишем данное в условии значение площади и получим уравнение на оставшийся параметр:

| | 32= ||∫ x2(3x2− 6x+ q)dx||=||(x3− x3− 3(x2 − x2)+q(x − x))||= |x1 | 2 1 2 1 2 1

| | | | = |(x2− x1)(x21 +x22+ x1x2 − 3x1− 3x2 +q)|=|(x2 − x1)((x1+x2)2− x1x2− 3(x1+ x2)+q)|=

|| 2q|| |||∘---4q 2q||| (∘ ---q)3 = ||(x2− x1)(−2+ 3-)||= || 4− -3 (2− 3-)||= 4 1− 3

(∘---q)3 8= 1 −3

q 4= 1− 3

q = −9

Ответ:

$p =−3,q = −9$

Ошибка.
Попробуйте повторить позже

Задача 11#83310

На графике приведенного квадратного трехчлена с целыми коэффициентами отмечены две точки с целочисленными координатами. Найти расстояние между этими точками, если известно, что оно выражается целым числом, а дискриминант квадратного трёхчлена равен 9.

Источники: Росатом - 2024, региональный вариант, 11.5 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Формула подсчёта расстояния между двумя данными точками использует квадрат этого расстояния. Тогда что мы можем сказать про квадрат числа, если корень из него — целочисленное значение?

Подсказка 2

Выражение квадрата расстояния содержит сразу и абсциссы, и ординаты наших точек, это очень много переменных, вот бы оставить что-то одно из этого. Откуда же тогда можно получить y₁ - y₂ и x₁ - x₂ в одном выражении (где x₁, x₂, y₁, y₂ — абсциссы и ординаты данных точек соответственно)?

Подсказка 3

Тогда квадрат расстояния — это (x₁ - x₂)2(1 + k²), где k — некоторое выражение, записанное сейчас одной переменной для удобства. Имеется выражение «квадрат = 1 + квадрат», но много ли квадратов целых чисел отличаются на 1? Какой вывод можно сделать об абсциссах данных точек и о вершине параболы?

Подсказка 4

Осталось ещё одно условие в задаче, про дискриминант. Если изначальный квадратный трёхчлен равен y = x² + bx + с. В дискриминанте задействованы b и c, а в предыдущем найденном факте мы упоминали вершину, что их связывает? Конечно же b! А после можно будет сделать вывод на чётность x₁ - x₂.

Показать ответ и решение

Пусть $(x ,y ),(x ,y ) 1 1 2 2$ — эти точки, а $y =x2 +bx+ c$ — трёхчлен. Тогда справедливы равенства $y = x2+ bx + c 1 1 1$ и $y = x2 +bx + c 2 2 2$ . Если вычесть из первого второе, то получим $y1− y2 =(x1− x2)(x1 +x2+ b)$ , то есть $y1− y2$ делится на $x1− x2$ (для удобства запишем $y1− y2 = k(x1− x2)$ ).

Квадрат расстояния равен

2 2 2 2 (y1− y2) + (x1− x2) =(x1− x2) (1 +k )

Поскольку множитель $(x − x )2 1 2$ — квадрат, то и $1+ k2$ должен быть квадратом. Заметим, что квадраты целых чисел могут отличаться на $1$ только если эти числа — $1$ и $0$ . Значит, $k =0 =x + x + b 1 2$ , откуда $y − y =0 1 2$ . То есть абсциссы выбранных точек симметричны относительно абсциссы вершины параболы.

Поскольку $2 b − 4c$ равен 9, то $b$ нечётное. Таким образом, абсцисса вершины параболы является полуцелым числом (рациональная дробь со знаменателем $2$ ), а значит, абсциссы $x1$ и $x2$ разной чётности, то есть расстояние — любое положительное нечётное число.

Ответ: Это может быть любое положительное нечётное число.

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#83311

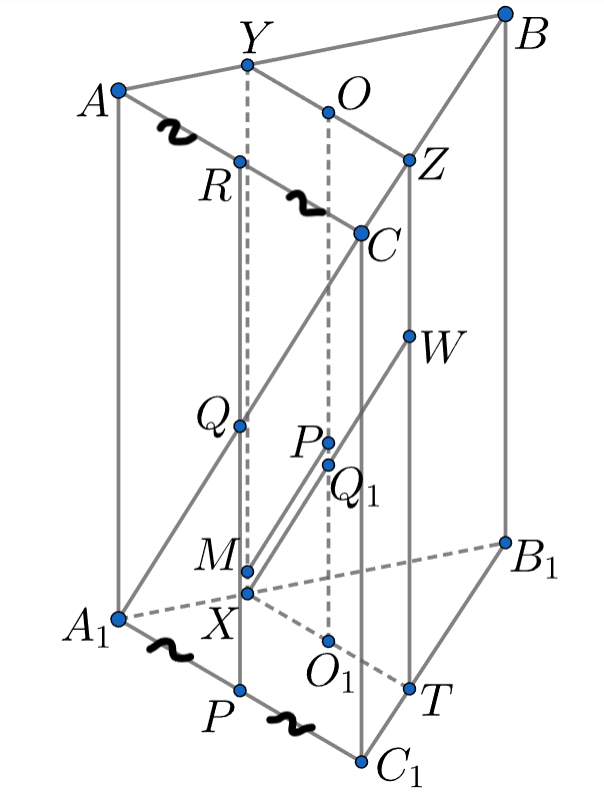
Медианы оснований треугольной призмы $ABCA B C 1 1 1$ пересекаются в точках $O$ и $O 1$ соответственно. На отрезке $OO 1$ взята точка $P$ так, что $O1P :PO = 3:5$ . Через точку $P$ проведена прямая параллельная диагонали $A1C$ боковой грани призмы. Найти длину отрезка этой прямой, расположенного внутри призмы, если длина диагонали $A1C$ равна 2.

Источники: Росатом - 2024, региональный вариант, 11.6 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Рассмотрим сечение призмы XYZT, проходящее через OO₁ и параллельное грани ACC₁A₁. Прямая, проходящая через точку Р и параллельная А₁С, будет лежать как раз в этом сечении. А искомый отрезок - это часть этой прямой, ограниченная четырехугольником XYZT. А какой фигурой является XYZT? Как относятся ее стороны к сторонам призмы?

Подсказка 2

Верно, XYZT - параллелограмм. ZT = XY = A₁A, XT = YZ = 2/3 * AC, так как точка пересечения медиан делит медианы в отношении 2 к 1. Теперь нужно подумать, с помощью чего мы можем "перенести" плоскость ACC₁A₁ на плоскость XYZT?

Подсказка 3

С помощью гомотетии! Сделаем гомотетию в точке В₁ с коэффициентом 2/3. Подумайте, куда перейдут точки, лежащие в плоскости ACC₁A₁.

Подсказка 4

Например, точка А₁ перейдет в точку Х. Постройте прямые, параллельные А1С, через точки Х и Z. Чему будут равны отрезки этих прямых, отграниченные параллелограммом XYZT? Равна ли искомая прямая этим отрезкам?

Показать ответ и решение

Рассмотрим сечение призмы $XY ZT$ , проходящее через $OO 1$ и параллельное грани $ACC A 1 1$ . Это параллелограмм, а $OO 1$ — его средняя линия.

Сделаем гомотетию в точке $B1$ с коэффициентом $2 3$ . Тогда точки $A1$ и $C1$ перейдут в $X$ и $T$ , потому что точка пересечения медиан делит медиану в отношении $2$ к $1$ . Точка $Q$ перейдёт в точку $Q1$ , делящую отрезок $OO1$ в отношении $2$ к $1$ (до гомотетии отрезок $P Q$ был половиной $PR$ , а после он перешёл в $XQ1$ , который равен $1 3PR$ ). При этом прямая $XQ1$ будет пересекать отрезок $TZ$ в точке $W$ , поскольку в параллелограмме $ACC1A1$ прямая $A1C$ пересекает вершину $C$ , а в параллелограмм $XYZT$ отличается от $ACC1A1$ лишь тем, что длины сторон $YZ$ и $XT$ короче, а значит, точка пересечения прямой $XQ1$ с прямой $TZ$ будет лежать ниже точки $Z$ .

$PIC$

Аналогично, прямая, проходящая через $Z$ параллельно прямой $A1C$ будет делить $OO1$ в отношении $2$ к $1$ , но уже считая от точки $O$ , и она будет проходить через отрезок $XY$ . Значит, прямая $MP$ будет лежать между этими двумя прямыми и также проходить через отрезок $TZ$ . Значит, отрезок нужной прямой — это отрезок прямой $MP$ , содержащийся в параллелограмме $XY ZT$ .

Поскольку $MP ∥ XW$ , длина этого отрезка будет равна $XW$ . Отрезок $XQ1$ — образ $AQ$ при гомотетии, значит, он равен $23AQ = 23$ .

Также $XQ1 = Q1W$ , то есть искомая длина — $43$ .

Ответ:

$4 3$

Ошибка.
Попробуйте повторить позже

Задача 13#88137

Найдите сумму максимальных нечётных делителей всех чисел от 601 до 1200 включительно.

Источники: по мотивам Росатома - 2024, 11.3

Подсказки к задаче

Подсказка 1

Зададимся вопросом, что означает тот факт, что у двух чисел из отрезка [601; 1200] одинаковый наибольший нечётный делитель. Если это так, как могут отличаться эти два числа?

Подсказка 2

Если у двух чисел одинаковый наибольший нечётный делитель, то состав нечётных простых, в них входящих, идентичен у двух чисел, и отличаться эти числа могут только степенью вхождения двойки. Может ли такое случиться для двух чисел из данного отрезка?

Подсказка 3

Такая ситуация невозможна, ведь на отрезке нет чисел, которые отличаются друг от друга хотя бы в два раза. Какой вывод можно сделать из этого рассуждения?

Подсказка 4

Тогда мы получили, что искомые делители у всех наших чисел различны. Делитель не может быть больше самого числа, поэтому мы не получим делители, превосходящие 1200. Тогда не остаётся выбора, какие нечётные числа брать :)

Показать ответ и решение

Пусть $S =a +a + ...+a 601 602 1200$ — сумма максимальных нечётных делителей чисел на отрезке $[601,1200]$ , причём $a i$ является максимальным нечётным делителем числа $i$ для всех $i∈{601,602,...,1200}.$

Пусть $n$ — натуральное нечётное число на отрезке $[1;1200].$ Докажем, что $n$ совпадает с $aj$ для некоторого $j ∈ {601,602,...,1200}.$ Предположим противное. Рассмотрим ряд

2 n,2n,2 n,...

Поскольку $n< 601,$ то существует неотрицательное число $i$ такое, что $2in <601,$ а $2i+1n >1200,$ что невозможно.

Таким образом, каждое нечётное число на отрезке $[1;1200]$ совпадает с $a j$ для некоторого $j ∈ {601,602,...,1200}$ . Осталось заметить, что на отрезке $[1,1200]$ каждое второе число является нечётным, следовательно, количество нечётных чисел равно 600, ровно из стольких слагаемых состоит $S$ , то есть никаких других чисел там нет. Наконец, по формуле суммы членов арифметической прогрессии

1200 1+ 3+...+1199= 1200⋅-4--= 1200⋅300= 360000.

Ответ: 360000

Ошибка.
Попробуйте повторить позже

Задача 14#94430

Натуральное число $n ≥2024$ имеет простой делитель $p >3$ и другой делитель $q,$ связанный с $p$ соотношением

(p− 1)(q+ 3)= n− 3

Найти наименьшее возможное при эти этих условиях число $n.$

Показать ответ и решение

Раскроем скобки:

pq− q+3p= n

(1)

По условию, $p$ — делитель числа $n,$ поэтому из $(1)$ следует, что $q$ делится на $p.$ Следовательно, $q = kp,$ $q$ — делитель $n,$ поэтому из $(1)$ следует, что $3p$ делится на $q.$ Следовательно, $k =3⇒ q = 3p$ (случай не $k= 1$ подходит, так как $p ⁄=q).$ Тогда, следуя $(1),$ получаем, что $n =3p2.$ Теперь следует выбрать минимальное простое число $p,$ для которого $3p2 ≥ 2024.$ Таким простым числом является $p =29⇒ n = 2523.$

Ответ:

$2523$