Тема ОММО - задания по годам

ОММО 2022

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела оммо - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#34678

Точка $O$ является центром окружности, описанной около треугольника $ABC$ со сторонами $BC = 8$ и $AC = 4$ . Найдите длину стороны $AB$ , если длина вектора $−→ −−→ −−→ 4OA −OB − 3OC$ равна $10$ .

Подсказки к задаче

Подсказка 1

В таких задачах на счет нужно очень четко понять, какие переменные мы вводим и зачем это делать. Какие переменные у нас уже известны? Две стороны треугольника. Значит, если попробовать выразить наше выражение векторное, через часть из известных переменных и того, что нам нужно найти, то может что-то получится.

Подсказка 2

Давайте выразим каждый из векторов в выражении через векторы CA и AB, тогда выходит, что |3AC + AB| = 10 (здесь написаны векторы). Далее, нам ничего не остается как возводить в квадрат, но там вылезет косинус из произведения векторов. Как побороть эту проблему, если у нас в виде переменных остаются AB и cos(BAC).

Подсказка 3

Конечно, у нас есть cos(BAC) и AB, значит все намекает на теорему косинусов для треугольника ABC и стороны BC. Вычтя из нашего равенства, которое получилось возведением в квадрат модуля, равенство из теоремы косинусов, получим уравнение, в котором есть AB*cos(BAC), приравненное к константе. Что тогда можно сделать, чтобы найти AB?

Подсказка 4

Само собой, остается подставить это в уравнение, полученное из модуля, так как после подстановки, там останется одна неизвестная - AB, а значит, задача решена!

Показать ответ и решение

$PIC$

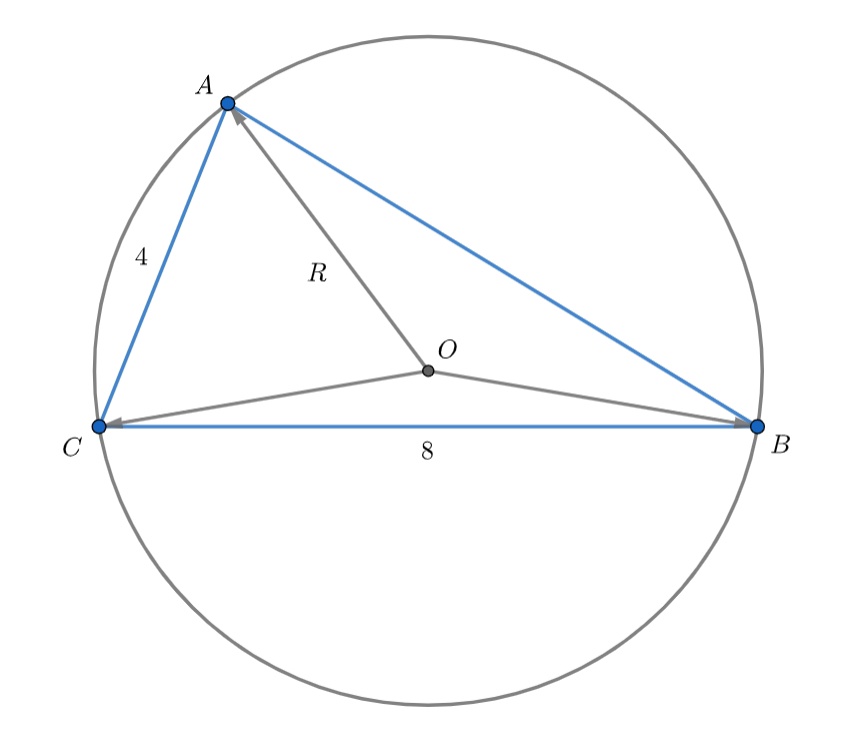
Будем пользоваться тем, что скалярный квадрат вектора равен квадрату длины вектора.

Из условия получаем, что

|3−−→CO+ 3−O→A +−B−→O + −O→A|= 10

−→ −→ |3CA+ BA|= 10

−→ −→ |3AC+ AB|= 10

А теперь возведём обе части в квадрат:

9AC2+ AB2 +6AC ⋅AB⋅cos∠BAC = 100

По теореме косинусов из треугольника $ABC$ имеем

2 2 2 AC + AB − 2AC ⋅AB ⋅cos∠BAC = BC

Вычитая это равенства из полученного выше, получаем

8AC2+ 8AB ⋅AC ⋅cos∠BAC =100− BC2

С учётом $AC = 4,BC = 8$ имеем

8⋅16+ 8⋅AB ⋅4⋅cos∠BAC = 36

8AB ⋅cos∠BAC =9− 32

Подставим в $2 2 2 AC + AB − 2AC ⋅AB ⋅cos∠BAC = BC :$

2 16+ AB +23= 64

AB =5

Ответ:

$5$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#41306

Докажите, что для каждого натурального числа $n$ число

2n n+2 n 5 + 3 + 3

делится на $11.$

Источники: ОММО-2022, номер 1, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Какое слагаемое из этой суммы выбивается сильнее других? Как можно его исправить?

Подсказка 2

Сильнее других выбивается 5^2n. При этом мы рассматриваем выражение по модулю 11(так как хотим, чтобы на 11 делилось выражение). Как исправить 5^(2n), чтобы оно имело такой же вид, как и другие слагаемые?

Подсказка 3

Рассмотреть сравнение 5^2 = 3(mod 11). В таком случае можно возвести сравнение в степень n и подставить в изначальное выражение, то есть заменить 5^(2n) на выражение с тем же остатком по модулю 11

Показать доказательство

Первое решение.

Поскольку $2 5 ≡113$ , то по модулю $11$ имеем

n n n n 3 + 9⋅3 + 3 = 11⋅3 ≡11= 0

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Докажем утверждение задачи для целых неотрицательных $n$ индукцией по $n.$

База: Если $n =0,$ то $52n+ 3n+2 +3n =50+ 32+30 = 11$ — делится на $11.$

Переход: Предположим, что при $n = k$ число $52n +3n+2+ 3n = 52k+ 10⋅3k$ делится на $11,$ и докажем, что при $n= k+ 1$ число $52n+ 3n+2 +3n = 52k+2 +10⋅3k+1$ также делится на $11.$ Заметим, что

( ) 52k+2+10⋅3k+1 = 3⋅ 52k+ 10⋅3k + 22⋅52k

Первое слагаемое в правой части делится на $11$ по предположению индукции, а второе — потому что содержит множитель $22.$ Значит, и вся сумма делится на $11.$ Переход доказан.

Ошибка.
Попробуйте повторить позже

Задача 3#49764

Функция $F$ определена на множестве троек целых чисел и принимает действительные значения. Известно, что для любых четырёх целых чисел $a,b,c$ и $n$ выполняются равенства $F (na,nb,nc)= n⋅F(a,b,c),F(a+ n,b+ n,c+n)= F(a,b,c)+n$ , $F (a,b,c)= F(c,b,a)$ . Найдите $F(58,59,60).$

Источники: ОММО-2022, номер 9, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Давайте посмотрим на нашу функцию и на то, что с ней можно делать. Во-первых, можно выносить общий множитель из аргумента. Во вторых, можно вычитать, прибавлять что угодно и к аргументам функции, и к её значению, при этом равенство останется верным. Ещё наша функция симметрична относительно первой и второй переменной. Теперь подумаем, как нам можно получить F(58,59,60). Это три последовательных числа. Значит, чтобы получить значение на этих значениях, мы можем найти значение в точке F(k-1,k,k+1) и потом по второму свойству найти требуемое. При этом как-то надо воспользоваться двумя другими условиями. Попробуйте подобрать такое k, чтобы значение в нём можно было бы найти с помощью двух других условий.

Подсказка 2

Если вы еще не нашли такое k, то давайте вместе подумаем, каких бы свойств нам хотелось бы от k. Во-первых, надо, чтобы оно определялось (то есть его значение становилось известным) только через первое и третье условие, так как если оно известно через второе, то это нам не подходит, поскольку тогда либо существует тройка, значение которой определяется через первое и третье условие, либо все значения определяются через второе, однако последнее, очевидно, неверно. Значит, существует тройка, которая определяется через первое и третье. Поскольку оба этих условия не дают свободного члена, то единственное, что мы можем получить из этих уравнений - это 0, поскольку, если мы получим равенство двух значений, без свободного члена, то это будет их отношение и , коль скоро, мы не используем второе выражение, то единственное отношение, которое можно получить и найти значение функции в точке - это 0. Значит, нам нужно получить 0. Значит, с одной стороны функция равна себе, а с другой стороны минус себе. Попробуйте что-то с этим сделать.

Подсказка 3

Если мы хотим, чтобы функция в точках была равна минус себе, то так как n*F(a,b,c) = n*F(c,b,a) = F(na,nb,nc), мы хотим, чтобы na = -nc, nb = - nb, nc = -na. Но из второго равенства следует, что nb=0, а значит и b = 0(иначе, n = 0, и у нас просто функция от нулей равна 0. Что не подходит нам под условие на k-1,k,k+1. Значит, b = 0, a = -1, c = 1. И значит, F(-1,0,1)= 0 = F(58,59,60) - 59.

Показать ответ и решение

Заметим, что для $n= −1$

F(−1,0,1)= F(1,0,−1)= (−1)⋅F(−1,0,1) =⇒ F (− 1,0,1)= 0

Отсюда легко видеть $F(58,59,60)= F(−1,0,1)+59 =59.$

Ответ:

$59$

Ошибка.
Попробуйте повторить позже

Задача 4#71523

Группа авантюристов показывает свою добычу. Известно, что ровно у 13 авантюристов есть рубины; ровно у 9 — изумруды; ровно у 15 — сапфиры; ровно у 6 — бриллианты. Кроме того, известно, что

если у авантюриста есть сапфиры, то у него есть или изумруды, или бриллианты (но не то и другое одновременно);
если у авантюриста есть изумруды, то у него есть или рубины, или сапфиры (но не то и другое одновременно).

Какое наименьшее количество авантюристов может быть в такой группе?

Источники: ОММО-2022, номер 2 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Внимательно посмотрим на условие: рассмотрим авантюристов, у которых есть сапфиры! На какие группы мы можем их разделить?

Подсказка 2

Обладателей сапфиров столько же, сколько суммарно обладателей изумрудов и бриллиантов. Теперь посмотрим на второе условие. Мы знаем, какие камни есть у тех, кто обладает изумрудами. Кто тогда обладает рубинами и как это влияет на общее количество человек?

Подсказка 3

Заметим, что есть 9 обладателей сапфиров и изумрудов и 6 обладателей сапфиров и бриллиантов. Тогда 13 обладателей рубинов никак не могут пересекаться с девятью обладателями изумрудов!

Показать ответ и решение

Заметим, что количество авантюристов, у которых есть сапфиры, равняется суммарному количеству авантюристов, у которых есть изумруды или бриллианты. Тогда из первого условия следует, что у 9 авантюристов есть сапфиры и изумруды, а у 6 — сапфиры и бриллианты. Т.е. у каждого авантюриста, у которого есть изумруды, обязательно есть сапфиры. Тогда, из второго условия, не может быть авантюриста, у которого есть и изумруды, и рубины. Значит, авантюристов как минимум $13+ 9= 22.$

Столько авантюристов и правда может быть: пусть у нас есть 9 авантюристов, у которых есть сапфиры и изумруды, 6 авантюристов, у которых есть сапфиры, бриллианты и рубины, а также 7 авантюристов, у которых есть только рубины. Можно убедиться, что этот пример подходит под все условия.

Ответ: 22

Ошибка.
Попробуйте повторить позже

Задача 5#71524

Бригада рабочих трудилась на заливке катка на большом и малом полях, причем площадь большого поля в 2 раза больше площади малого поля. В той части бригады, которая работала на большом поле, было на 4 рабочих больше, чем в той части, которая работала на малом поле. Когда заливка большого катка закончилась, часть бригады, которая была на малом поле, еще работала. Какое наибольшее число рабочих могло быть в бригаде?

Источники: ОММО-2022, номер 3 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Исходя из условия сразу можно с помощью переменных выразить, сколько человек в каждой части бригады(через n), какова производительность групп, площадь катка и время работы.

Подсказка 2

Запишем неравенство по условию: S/an > 2S/(a(n+4)). Осталось лишь его решить и оценить n.

Показать ответ и решение

Обозначим число рабочих на меньшем поле как $n,$ тогда их количество на большем поле равно $n+ 4,$ а всего в бригаде $2n+ 4$ человека. В условии задачи предполагается, что производительность каждого рабочего одинаковая, обозначим ее $a.$ Соответственно, производительности каждой части бригад равны $an$ и $a(n+ 4).$ Если площадь малого поля $S,$ то площадь большого равна $2S.$ Время, затраченное на выполнение всей работы каждой из бригад, соответственно равно

S 2S an и a(n-+4)

По условию задачи

-S > --2S-- an a(n +4)

В силу положительности всех переменных, это неравенство равносильно неравенству

n +4 >2n ⇔ n< 4

Поэтому $n ≤3,$ следовательно, $2n+ 4≤ 10.$ Ситуация равенства, очевидно, возможна: достаточно взять любые положительные $S$ и $a.$

Ответ: 10

Ошибка.
Попробуйте повторить позже

Задача 6#71525

Решите в действительных числах систему уравнений:

(| a+ c= 4 |||{ ac+ b+d =6 | |||( ad+ bc =5 bd= 2

Источники: ОММО-2022, номер 5 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Перед нами система с 4 неизвестными, в которой, если начать выражать всё последовательно, ничего хорошего не выйдет. Давайте немного повспоминаем, где такая конструкция встречается? Возможно, вы этим занимались в алгебре.

Подсказка 2

Ага, если вспомнили, то отлично. Если нет, то ничего страшного. Попробуйте перемножить два приведённых трёхчлена с коэффициентами a, b, c и d и привести подобные слагаемые. Не видите сходств? Какой вывод отсюда можно сделать?

Подсказка 3

Да, нам по сути сказали коэффициенты многочлена 4 степени! Видеть такое вы могли в методе неопределённых коэффициентов как раз для уравнения 4 степени. Теперь вы можете попробовать найти очевидные корни этого многочлена и разложить его на скобки. Теперь осталось понять главное. Для чего вы всё это делали?

Подсказка 4

Точно, для того, чтобы понять, что корни будут единственными. Вы могли и просто так угадать a, b, c и d, но о единственности ничего утверждать не могли. Осталось только сопоставить наши изначальные квадратные трёхчлены с тем, что получилось в итоге, и победа!

Показать ответ и решение

Пусть $x2+ ax+ b$ и $x2 +cx+ d$ — два квадратичных многочлена, коэффициенты которых — искомые корни данной системы. Тогда

( 2 )( 2 ) 4 3 2 x + ax+ b x + cx +d = x + (a +c)x +(ac+b+ d)x +(ad+bc)x +bd=

4 3 2 = x +4x + 6x +5x+ 2

Из делителей свободного коэффициента $2$ находим корни $− 1$ и $− 2$ , тогда можно поделить многочлен на $(x+ 1)(x+ 2)=(x2+ 3x +2):$

x4+ 4x3 +6x2+ 5x+2 =(x2+ 3x+ 2)(x2+ x+ 1),

что возможно только в двух случаях:

{ { x2+ax +b= x2+ 3x+2 x2 +ax+ b= x2+ x+1 x2+cx+ d= x2+ x+ 1 или x2 +cx+ d= x2+3x +2

тогда в первом случае получаем $a= 3,b= 2,c= 1,d =1,$ а во втором — $a= 1,b=1,$ $c= 3,d= 2.$

Ответ:

$(3,2,1,1),(1,1,3,2)$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#71526

Решите уравнение

x√11- x√11- 5x√11 arcsin 2√21-+ arcsin4√21 = arcsin-8√21-

Источники: ОММО-2022, номер 6 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

В первую очередь, когда в задаче мы видим тригонометрические функции, нужно сразу вспоминать про ограничения на аргументы.

Подсказка 2

Когда мы найдём ограничения на x, можно использовать стандартную идею в арктриге, давайте возьмём прямую функцию от обратных. В нашем случае, функцию синуса от правой и левой части уравнения.

Подсказка 3

В правой части всё легко и понятно, но вот с левой явные проблемы. Давайте обратим внимание на то, что слева у нас ни что иное, как синус суммы. Распишем его по формуле.

Подсказка 4

Воспользуемся тем, что cos(arcsin(t)) = √(1-t²). После чего получаем уравнение, которое при вынесении общего множителя разобьётся на два случая, когда x = 0(не забудьте проверить, что он подходит), а так же на второй случай, когда x≠0.

Подсказка 5

Во втором случае получается уравнение √(336-11x²) + √(84-11x²) = 5√21. Ограничения на x, которые мы считали в начале, тут нам помогут в утверждении, что подкоренные выражения положительные. Если несколько раз использовать тот факт, что правая и левая часть положительны и мы можем их возводить в квадрат, то дорешать уравнение не составит труда, главное, не забудьте проверить, что корни уравнения подходят.

Показать ответ и решение

Из условия на область определения арксинуса вытекает, что

8√21- 1344 |x|≤ 5√11-⇔ x2 ≤ 275

(1)

Вычисляя синус от обеих частей уравнения и учитывая, что

cosarcsint> 0

и, следовательно,

∘ ----- sin(arcsint)=t, и cos(arcsint) = 1− t2,

получаем

√-- ∘ -------- √ -- ∘------- √ -- x√11⋅ 1− 11x2-+ x√-11⋅ 1 − 11x2 = 5x√-11 2 21 16 ⋅21 4 21 4 ⋅21 8 21

Перенося все в левую часть уравнения, упрощая и вынося общим множитель за скобки, имеем

√-- x-11 (∘336-−-11x2+ ∘84−-11x2− 5√21) =0 8⋅21

Из данного уравнения следует, что или $x =0$ (который, очевидно, подходит), или $x$ является корнем уравнения

∘336−-11x2+ ∘84-− 11x2 = 5√21

Из условия $(1)$ следует, что все подкоренные выражения положительны. Поскольку обе части уравнения положительны, то их можно возвести в квадрат

∘ ------------------ 336− 11x2+ 2 (336− 11x2)(84− 11x2)+ 84− 11x2 = 525

Перенося всё кроме корня в правую часть уравнения, имеем

2∘ (336−-11x2)(84−-11x2)= 22x2+ 105

Возводя ещё раз обе части уравнения в квадрат, получаем

( 2)( 2) 4 2 4 336− 11x 84 − 11x = 484x + 4620x + 11025

или

23100x2 = 101871

Таким образом, уравнение имеет ещё два возможных корня

x =± 21 10

Проверка. Проверяем, что левая часть уравнения при данных значениях аргумента лежит в промежутке $[−π∕2;π∕2].$ Для этого вычисляем косинус левой части

( x√11 x√11) ∘ (---11x2)(----11x2)- 11x2 cos arcsin2√21 +arcsin 4√21 = 1− 4⋅21 1− 16-⋅21- − 8⋅21 =

∘ ---------------------- ( 11⋅21)( -11-⋅21-) 11⋅21 13⋅37 11⋅21 = 1− 4⋅100 1− 16⋅100 − 8⋅100 = 800 − 800 > 0

Поскольку значения косинуса положительно, а левая часть лежит в промежутке $[−π;π],$ то она лежит в промежутке $[− π∕2;π∕2].$ Значит, все найденные числа являются решением задания.

Ответ:

$0;±21 10$

Ошибка.
Попробуйте повторить позже

Задача 8#71527

При каких значениях параметра $a$ уравнение

2 log2x +(a− 6)log2 x+9 − 3a= 0

имеет ровно два корня, один из которых в четыре раза больше, чем другой?

Источники: ОММО-2022, номер 7 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Решать параметр с логарифмом совсем как-то не хочется. Какое первое действие можно сделать сразу?

Подсказка 2

Верно, можно просто сделать замену логарифма и решать для начала квадратное уравнение с параметром. В таких случаях очень полезно бывает проверить, не имеет ли наше уравнение очевидных корней? Угадать их помогает разложение свободного члена и теорема Виета.

Подсказка 3

Ага, корни нашего уравнения 3 и 3-a. Осталось только сделать обратную замену, выполнить условие задачи, и победа!

Показать ответ и решение

Пусть $t= log x, 2$ тогда уравнение принимает вид

2 t+ (a− 6)t+ (9− 3a)=0

Заметим, что

3⋅(3− a)= 9− 3a,3+ (3− a)= 6− a

Отсюда по теореме, обратной теореме Виета, корни этого уравнения $− 3$ и $3− a.$ Делаем обратную замену:

[ log2x= 3 [ x= 8 log2x= 3− a ⇒ x= 23−a

Получаем два случая:

[ [ 8 =4⋅23−a ⇒ a= 2 23−a = 4⋅8 a= −2

Ответ:

${−2;2}$

Ошибка.
Попробуйте повторить позже

Задача 9#71528

В треугольнике $ABC$ сторона $AC = 42.$ Биссектриса $CL$ делится точкой пересечения биссектрис треугольника в отношении $2 :1,$ считая от вершины. Найдите длину стороны $AB,$ если радиус вписанной в треугольник $ABC$ окружности равен 14.

Источники: ОММО-2022, номер 8 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Вот у нас есть уже одна биссектриса и центр вписанной окружности. Попробуйте рассмотреть биссектрису из точки A, но только не в треугольнике ABC, а в треугольнике ALC) Чем здесь можно воспользоваться?

Подсказка 2

Например, свойством биссектрисы про отношение сторон) Из этого будет следовать, что AL = 21. Теперь попробуйте понять, как можно выразить синус угла A..

Подсказка 3

Различным выражением площади треугольника ALC) Ведь с одной стороны это просто формула площади через синус и две стороны, а с другой стороны, можно разбить треугольник на два: AIC и AIL. Но как удобнее найти их площади?

Подсказка 4

Площадь каждого можно найти с помощью радиуса вписанной окружности и сторон, ведь в этих треугольниках радиусы будут высотами!Так, мы находим синус А = 1, т.е. угол А прямой) А дальше просто обычный счет и использование свойства биссектрисы снова)

Показать ответ и решение

Пусть $I$ — центр вписанной в треугольник $ABC$ окружности (т.е. точка пересечения биссектрис). Заметив, что $AI$ — биссектриса, в треугольнике $ALC,$ в силу свойства биссектрисы треугольника имеем:

AC :AL= CI :IL =2 :1⇒ AL =AC ∕2= 21

Далее,

AC ⋅AL ⋅sin∠A = 2S△ACL = 2S△AIC + 2S△AIL = AC ⋅r+AL ⋅r= (AC + AL)⋅r,

где $r$ — радиус вписанной в треугольник $ABC$ окружности. Таким образом,

42⋅21⋅sin∠A =(42+21)⋅14⇒ sin∠A = 1⇒ ∠A = 90∘

В силу свойства биссектрисы $BI$ треугольника $CLB$ имеем

BC :BL =CI :IL= 2:1

Полагая $BL = x,$ имеем $BC = 2x.$ В силу теоремы Пифагора:

AC2 + AB2 = BC2

422+(21+ x)2 = (2x)2

x =35 ⇒ AB =x +21= 56

Ответ: 56

Ошибка.
Попробуйте повторить позже

Задача 10#71529

Пусть $B$ — множество действительных чисел, не содержащее $0$ и $1.$ Известно, что если $b∈ B,$ то $1∈ B b$ и $1− 1∈ B. b$ Может ли в $B$ быть ровно 1000 элементов?

Источники: ОММО-2022, номер 10 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

По факту, у нас есть операции x -> 1/x и x -> 1 - 1/x. Подумайте, какие и сколько чисел мы вообще сможем получить из одного числа x, применяя эти операции?

Подсказка 2

Если просто поприменять эти операции, то можно заметить, что получится только 6 чисел, если они все различные. А можно ли получить из них меньше различных?

Подсказка 3

Да, попробуйте приравнять какие-то из всех полученных чисел, и вы поймете, могут ли они совпадать, либо если они совпадают, то при каком x) А сколько различных чисел вышло уже в этом наборе?

Подсказка 4

3! А теперь подумайте: у нас все наборы по 6 чисел и один из трех...Можно ли получить тогда множество из 1000 чисел?)

Показать ответ и решение

Посмотрим на числа ${t,1,1− t,-1-, t-,t−1}. t 1−t t−1 t$ Пусть

1 α:x ↦→ x

1 x− 1 β :x↦→ 1− x = -x--

Заметим, что отображение $α$ переводит числа $t,1t,1 − t,1−1t,tt−1,t−1t$ в числа $1t,$ $t,1−1t,1− t,t−t1,t−t1$ соответственно, а отображение $β$ — в числа $t−1t ,1− t,tt−1,t,1t,11−t$ соответственно.

Кроме того, заметим, что

t−→ t− 1-−→-1--−→ 1− t−→ --t-−→ 1 β t β 1− t α β t− 1 β t

Поэтому если $t∈ B,$ то каждое из чисел $t,1,1− t, 1-,-t-,t−1 t 1−t t−1 t$ лежит в $B,$ причём этот набор переходит в себя под действием $α$ и $β.$

Может ли в этом наборе быть меньше шести чисел? Да, если некоторые совпадают. Не умаляя общности, можно считать, что одно из этих чисел равно $t$ . Тогда или $t= 1, t$ откуда $t= −1$ (т.к. $t⁄= 1$ по условию), или $t= 1− t,$ откуда $t= 1∕2$ , или $t= 1-, 1−t$ откуда $t2− t+1= 0$ — нет решений, или $t= -t-, t−1$ откуда $t=2$ (т.к. $t⁄= 0$ по условию), или $t= t−1, t$ откуда $t2− t+ 1= 0$ — нет решений. Итак, в наборе может быть меньше 6 чисел, только если это набор $1 {−1;2;2}.$