ИТМО 2021
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Кубический многочлен имеет три корня. Наибольшее его значение на отрезке достигается при
, а наименьшее при
.
Найдите сумму корней многочлена.
Источники:
Подсказка 1
Давайте в первую очередь обозначим наш многочлен в стандартном виде. И раз нам намекают про производную в условии, то найдём и её. Исходя из заданного условия, что мы можем сказать про нули производной?
Подсказка 2
Верно, числа 5 и 7 являются просто корнями квадратного трёхчлена, то есть нулями производной. Запишем это в виде разложения на множители. Давайте теперь вспомним, какая есть теорема, где мы знаем сумму корней многочлена через его коэффициенты?
Подсказка 3
Точно, это теорема Виета! Мы можем выразить через изначальные коэффициенты кубического многочлена сумму корней производной, а оттуда найти и нужную сумму корней.
Пусть многочлен имеет вид , откуда его производная
.
Так как наименьшее и наибольшее значения достигаются во внутренних точках отрезка, то по необходимому условию экстремума
производная в этих точках равна нулю, так что имеет корни
и
, так что можно записать
По теореме Виета сумма корней многочлена равна
, а сумма корней многочлена
равна
, откуда
находим
.
Ошибка.
Попробуйте повторить позже
Найдите сумму натуральных чисел от до
включительно, имеющих с числом
общие делители, большие
Источники:
Подсказка 1
В условии задачи сказано, что надо просуммировать числа от 1 до 3000, которые не взаимнопросты с 3000. Какие нам тогда числа не подходят, если 3000 = 2³ * 3¹ * 5³?
Подсказка 2
Это значит, что нам подходят числа, которые делятся на 2, или на 3, или 5. Давайте поймём, что если нам подходит число x, то подходит и число 3000-x. При том, все числа, которые подходят под условие выше, разбиваются на пары. Или почти все? А когда тогда посчитать их сумму?
Подсказка 3
Числа 3000 и 1500 не составляют те самые пары, а вот все остальные числа, подходящие под условия все таки разбиваются на пары. Это значит, что нам теперь достаточно найти количество таких чисел и домножить их на 3000 (учтя особую роль в этой сумме исключений выше). Как найти количество таких чисел? Мы ведь не можем просто сложить количество чисел кратных 2, 3 и 5 и получить ответ. У нас есть числа которые кратны сразу двум каким-то, а также числа, кратные сразу всем. Подумайте, как тогда считать их количество?
Подсказка 4
Мы можем посчитать с помощью формулы включений и исключений количество таких чисел, а именно сначала количество просто кратных какому-то, минус сумма кратных сразу двум и плюс сумма кратных всем трём. Получится 2200. Чему тогда равна наша сумма?
, то есть нас интересуют числа, деляющиеся на
или
Найдём сначала количество таких чисел. Для этого
воспользуемся принципом включений и исключений. Чётных чисел от
до
ровно
, кратных трём —
,
кратных пяти —
. Однако, если просто сложить числа 1500,1000 и 600 , мы посчитаем некоторые числа 2 раза, а именно, числа,
делящиеся на
и
, поэтому из полученной суммы надо вычесть
и
. Однако,
всё ещё неправильный ответ, Поскольку в этом выражение числа, имеющие все три простых
множителя, сначала считаются три раза, а потом их количество вычитается опять же три раза, поэтому надо снова добавить эти числа.
Количество таких чисел
, значит, количество чисел, имеющих с
общие делители и не превосходящих его, это
Заметим теперь, что если какое-то число имеет с числом
общие делители, то число
тоже имеет с
те же самые общие
делители. Значит, все интересующие нас числа, кроме чисел
и
разбиваются на пары с суммой
(числу 3000 в пару
пришлось бы сопоставить
а числу
само себя). Таких пар получаается
поэтому итоговый ответ
Замечание.
Числа, меньшие и взаимно простые с ним разбиваются на пары таким же образом, поэтому участники, знакомые с функцией
Эйлера, могли получить формулу для ответа в виде
Ошибка.
Попробуйте повторить позже
Палиндром — это слово, которое не меняется, если в нём переставить буквы в обратном порядке, например . Сколько
различных
-буквенных слов можно составить из букв
так, чтобы они не содержали палиндромов длины больше
Источники:
Подсказка 1
Что означает, что у нас есть палиндром? Это значит, что есть палиндром чётной длины или нечётной длины. А что следует из этого утверждения? Какое более просто условие на слово нам достаточно проверять, чтобы слово было свободно от палидромов?
Подсказка 2
Это значит, что не должно быть палиндрома длины 2 и длины 3. Ну отсутствие палиндрома длины 3, равносильно тому, что у нас буквы через 1 не совпадают. А отсутствие длины два, значит, что не совпадают соседние. Какое тогда условие равносильно отсутствию палиндромов длины 2 и 3?
Подсказка 3
Эти условия равносильны тому, что среди трёх подряд идущих букв нет совпадающих! Тогда остается простейшая комбинаторная задача на подсчёт количества вариантов!
Заметим, что две центральные буквы любого палиндрома чётной длины одинаковы, то есть образуют палиндром длины два. Точно так же
три центральные буквы палиндрома нечётной длины образуют палиндромы длины три. Таким образом, отсутствие в слове палиндромов
равносильно отсутствию палиндромов длины и
Это, в свою очередь, равносильно тому, что любые три подряд идущие буквы в слове
различны.
Первая буква в слове выбирается пятью способами, для следующей остаётся способа. Каждая из последующих букв не может
совпадать с двумя предыдущими, поэтому для неё остаётся
способа. Все эти числа надо перемножить, поэтому мы
получаем
Ошибка.
Попробуйте повторить позже
Положительные числа и
таковы, что
и
. Докажите неравенство
Источники:
Подсказка 1
Давайте для начала просто внимательно посмотрим на наше неравенство. Что мы можем сказать об этих выражениях? О коэффициентах? О переменных?
Подсказка 2
Интересно, что коэффициенты из левой части в сумме дают 1. Выглядит прямо как среднее арифметическое для чисел х, х, х, у, у и z... А тут ещё и неравенства...
Подсказка 3
Да, давайте применим здесь неравенство для среднего арифметического и геометрического! Преобразуем их с помощью известных условий и будем держать в голове, что x не больше z!
Заметим, что сумма коэффициентов в левой части равна единице. Применим неравенство для среднего арифметического и среднего
геометрического для чисел :
Поскольку и, следовательно,
Ошибка.
Попробуйте повторить позже
Вася выбрал четыре числа и для каждой пары вычислил логарифм большего по основанию меньшего. Получилось шесть логарифмов.
Четыре из них равны и
Какие значения может принимать наибольший из всех шести логарифмов?
Источники:
Подсказка 1
Не понятно, как рассуждать в нашей задаче не введя всё-таки 4 начальных упорядоченных числа x ≤ y ≤ z ≤ t. Понятно при этом, что мы можем выразить логарифм по основанию x от z через логарифмы по основанию x от y и логарифм по основанию y от z как их произведение. Какие тогда переменные удобно ввести, чтобы наши 6 чисел хорошо через них выражались?
Подсказка 2
Удобно ввести логарифмы с комбинациями "соседних" чисел. Тогда если они a, b, c в таком же порядке, как стоят начальные числа, то у нас есть числа a, b, c, ab, ac, bc, abc. Значит, мы свели задачу к поиску максимума среди них при условии того, что все числа больше 1 и известно 4 из них. Как тогда действовать? А если посмотреть на числа из условия?
Подсказка 3
Никакие два числа из условия в произведении двух не дают некоторое третье из условия. Это значит, что в любой тройке чисел из второй подсказки вида k, l, kl у нас хотя бы одно число неизвестно!
Пусть четыре исходные числа - это . Обозначим
. Тогда
,
то есть наши шесть логарифмов равны
и
Наибольший из них при этом
и именно его нам надо
найти.
Заметим, что среди наших четырёх логарифмов ни один не является произведением двух других. Это значит, что в каждой тройке
отсутствует хотя бы одно число. Каждое из шести чисел встречается ровно в двух из этих троек,
значит, чтобы “разрушить” все тройки, надо удалить два числа, которые вместе в одной тройке не встречаются, то есть, числа, которых мы
не знаем, это либо
и
, либо
и
, либо
и
.
Соответственно, у нас есть одна из четвёрок и
. Третий вариант невозможен, потому что ни одно из
наших четырёх чисел не является произведением трёх других. Для того, чтобы четвёрка чисел могла соответствовать первому или второму
вариантам, необходимо и достаточно, чтобы произведение двух чисел было равно произведению двух оставшихся. Это условие выполняется:
.
В первом случае мы имеем , и
— это наибольшее из наших четырёх чисел. Во втором случае
и
—
это как раз искомое произведение. Значит, мы имеем два возможных ответа:
и
Ошибка.
Попробуйте повторить позже
Четырёхугольник описан вокруг окружности с центром в точке
— точки касания сторон
и
соответственно,
и
— высоты в треугольниках
Найдите длину
отрезка
Источники:
Подсказка 1
На рисунке довольно много высот, но проведены они всё же не во всех появившихся треугольниках. Давайте проведем еще одну, KT в треугольнике OKA. Что можно сказать про точку T? Есть ли какая-то "красота" в нашем рисунке? ;)
Подсказка 2
T совпадает с S! Обратите внимание на то, что картинка довольно-таки симметричная:) Тогда имеет смысл найти равные углы по обе стороны от OA.
Подсказка 3
Что можно сказать про четырёхугольники KPOS и ORNS? Какие равенства из этого вытекают?
Подсказка 4
Отлично, углы SPO и ORS равны! А что мешает проделать те же действия относительно других радиусов из точки O? ;) Тогда у нас появится ещё больше пар равных углов!
Подсказка 5
Что можно сказать про четырёхугольник QPSR?
Подсказка 6
QPSR — параллелограмм! Тогда мы можем искать не QR ;) Осталось лишь придумать, как же через известные отрезки выразить тот, который мы хотим найти. Не забудьте о том, что у нас проведены высоты в прямоугольных треугольниках!
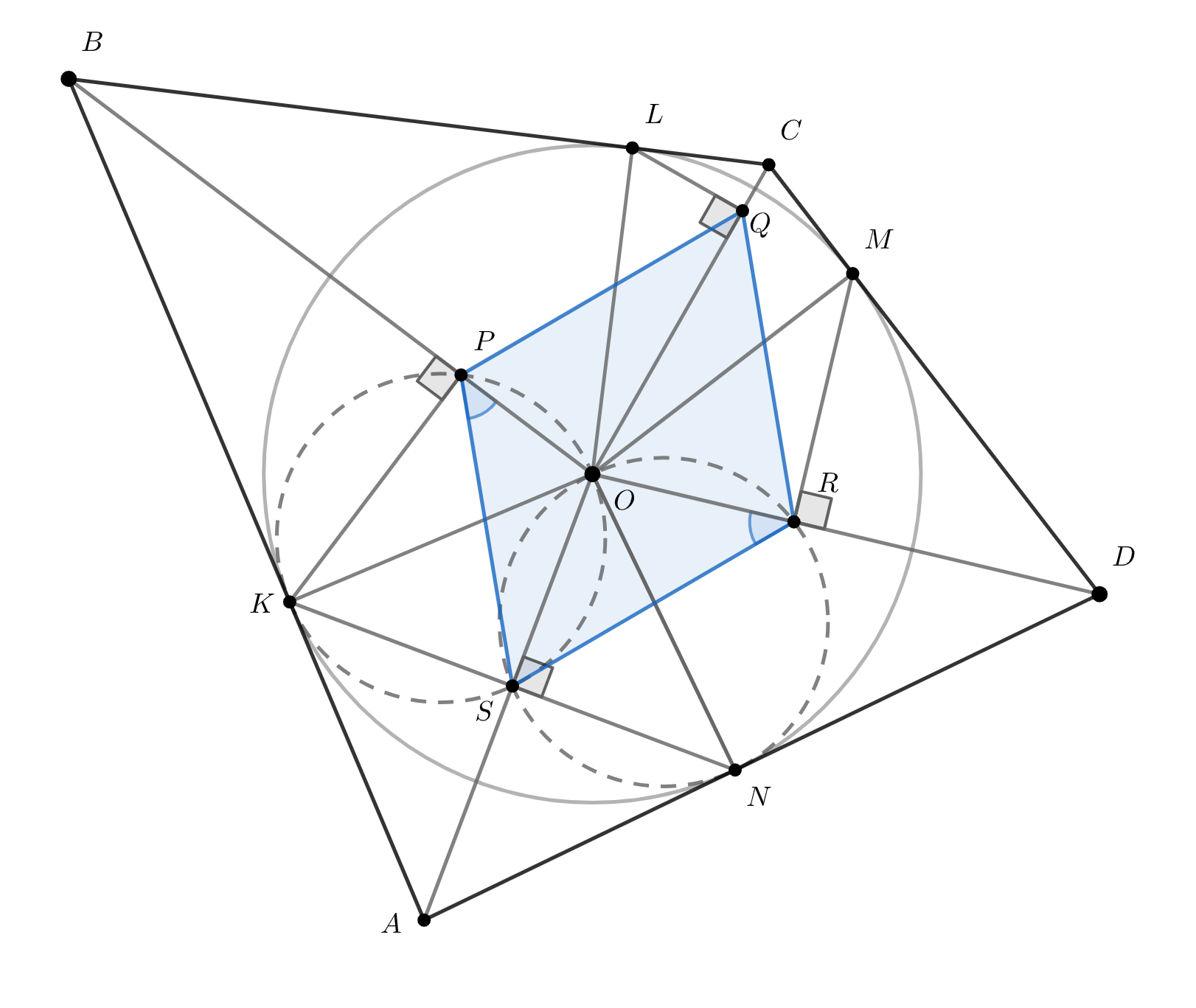
Треугольники и
— прямоугольные с общей гипотенузой и катетом, равным радиусу окружности, поэтому они равны. Значит,
их высоты падают в одну точку общей гипотенузы, то есть
— высота в треугольнике
. Поэтому точки
и
лежат на окружности с диаметром
. Аналогично точки
и
лежат на окружности с диаметром
. Поскольку
диаметры этих окружностей равны, градусные меры дуги
в этих окружностях совпадают. В первой окружности на эту
дугу опирается
, а во второй -
, значит, эти углы равны. (Именно равны, а не дополняют друг друга до
, потому что точки
и
лежат по разные стороны от прямой
, а окружности симметричны относительно
неё).
Аналогично . Сложив это с предыдущим равенством, получим
. Аналогично
, то есть
четырёхугольник
— параллелограмм.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание.
Можно понять, что вершины четырёхугольника инверсны вершинам четырёхугольника
относительно нашей
окружности, то есть мы только что повторили доказательство теоремы о том, что четырёхугольник, инверсный описанному, является
параллелограммом.
_________________________________________________________________________________________________________________________________________________________________________________
Значит, вместо длины отрезка мы можем найти длину отрезка
.
По свойству высоты прямоугольного треугольника, . Аналогично
, откуда
. Кроме того,
угол
в треугольниках
и
общий, поэтому они подобны с коэффициентом
. Значит,
Ошибка.
Попробуйте повторить позже
Два куба с ребром имеют общую грань. Сечение одного из этих кубов некоторой плоскостью — треугольник площади
Сечение
другого той же плоскостью — четырёхугольник. Какое наибольшее значение может принимать его площадь?
Источники:
Подсказка 1
Если вы правильно построили сечение, то плоскость должно пересекать кубы по треугольнику (будем его называть большим), на первый куб приходится треугольник (будем его называть маленьким), а на второй — трапеция. Притом площадь маленького треугольника фиксирована. Значит, максимизация площади трапеция равносильна максимизации площади большого треугольника, или же максимизации коэффициента подобия большого треугольника к маленькому.
Подсказка 2
Попробуйте выразить этот коэффициент с помощью теоремы Фалеса через некоторые отрезки, чтобы большинство отрезков были фиксированной длины. Тогда вы поймёте, какие отрезки нужно максимизировать или минимизировать.
Подсказка 3
Пусть есть треугольник, вершины которого расположены на трёх рёбрах куба на расстояниях x, y, z от вершины. Попробуйте записать его площадь в виде какого-то не очень сложного выражения от x, y, z, используя формулу Герона.
Подсказка 4
Если вы правильно исследовали коэффициент подобия и получили правильное выражение площади KPQ, то вы понимаете, что одну из переменных нужно минимизировать, а две остальные — максимизировать. Значит, две переменные будут равны ребру. Попробуйте выразить третью через длину ребра и коэффициент подобия, о котором говорили выше. И поставьте полученные выражения в формулу площади.
Пусть наши кубы — это и
с общей гранью
. Пусть также треугольное сечение первого куба —
это
, где точка
лежит на
, точка
на
, а точка
— на
. Одна из сторон четырёхугольного сечения второго
куба — отрезок
. Две другие — продолжения отрезков
и
на грани второго куба, назовём эти отрезки
и
. Чтобы
сечение было четырёхугольным, точки
и
должны находиться на одной грани второго куба, а это может быть только грань
.
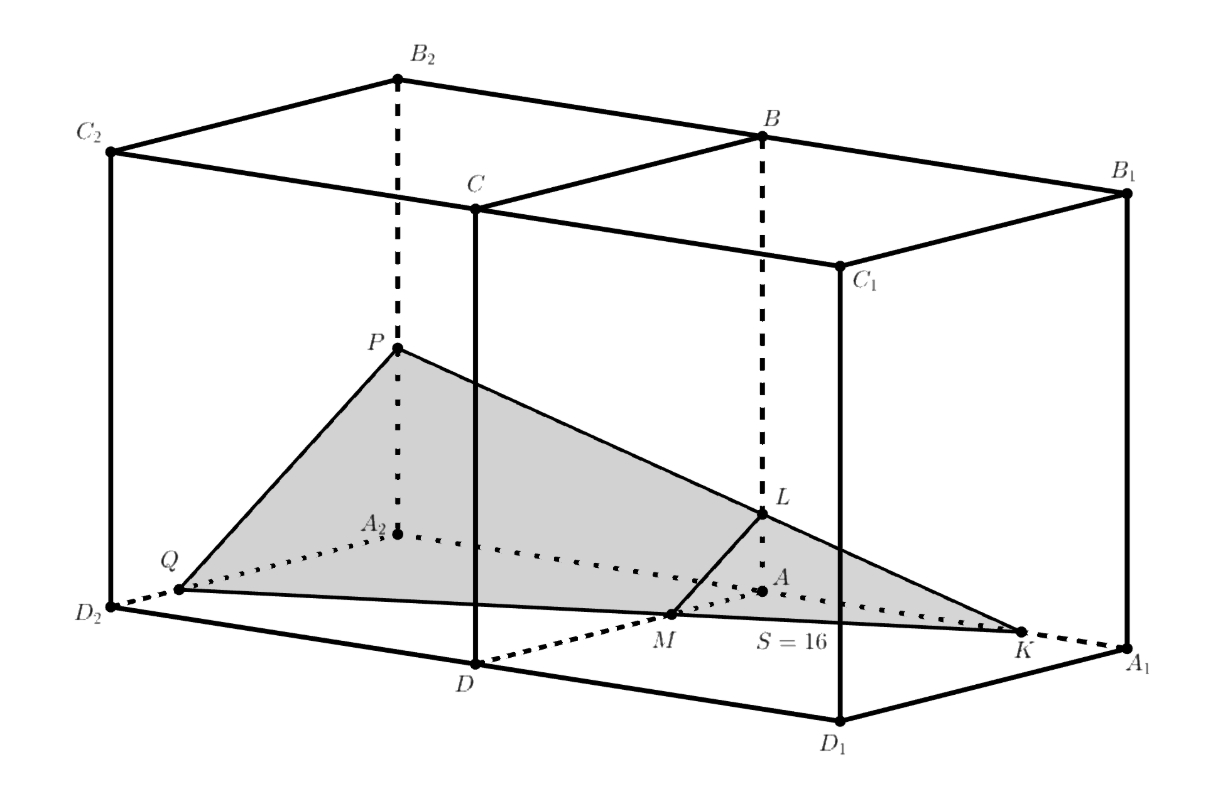
Значит, четырёхугольное сечение второго куба — это трапеция . Нахождение её наибольшей площади равносильно нахождение
наибольшей площади треугольника
, который подобен треугольнику
. Обозначим этот коэффициент подобия
. Тогда
. То есть наша задача равносильна задаче о нахождении максимального коэффициента
подобия.
С другой стороны, по теореме Фалеса . То есть коэффициент подобия тем больше, чем меньше
, а значит, наша задача — минимизировать
, или, что то же самое, минимизировать
.
Пусть у нас есть треугольник, вершины которого расположены на трёх рёбрах куба, выходящих из одной точки, на
расстояниях и
. Найдём формулу площади этого треугольника. Это можно делать по-разному, например, через
векторное произведение, или посчитав двумя способами площадь тетраэдра, образованного вершинами треугольника и
вершиной куба, но мы вычислим эту площадь по формуле Герона, зная стороны треугольника:
и
.
Посмотрим на эту формулу для треугольника и отрезков
. С одной стороны, нам надо
минимизировать
, а с другой - максимизировать площадь. Очевидно, для этого
и
должны быть максимальны, то есть равны ребру
.
Как мы знаем, , то есть
, откуда
Подставляя эти значения в формулу, получаем:
Соответственно,
откуда
Правая часть этого равенства убывает при , а значит, данное уравнение на
имеет не больше одного решения. Конкретное
решение в большинстве вариантов легко подбирается из этого равенства, так как оно целочисленное.
При мы получаем уравнение
откуда сразу возникает желание проверить , что оказывается верным.
Ответ получается как разность площадей двух треугольников и равен
Ошибка.
Попробуйте повторить позже
Гензель и Гретель играют в игру, Гензель ходит первым. Они по очереди ставят фишки на клетчатую доску (
строк и
столбцов).
Каждый раз, когда Гретель ставит фишку, она получает
очка за каждую фишку, уже стоящую в той же строке и
очка за каждую
фишку, уже стоящую в том же столбце.
На одной клетке может стоять только одна фишка. Игра заканчивается, когда все клетки доски заполнены.
Какое наибольшее количество очков может заработать Гретель вне зависимости от действий Гензеля?
Источники:
Подсказка 1
Предположим, что Гензель получает очки по тому же принципу. Тогда если мы выберем 2 клетки в одной линии, то тот, кто поставит в них фишку последним, заберёт свои очки за эту пару клеток. Может, у нас получится как-то посчитать общее количество очков, полученное за игру?
Подсказка 2
Верно, каждые две клетки в одном столбце дадут кому-то 4 очка, а в одной строке — 3 очка. Чтобы найти сумму набранных к концу игры очков, нужно просто посчитать количество пар клеток в строках и столбцах и сложить. Как Гретель заполучить как можно больше очков? После своего первого хода она может получить на 4 очка больше Гензеля... Как нам продолжить эту традицию?
Подсказка 3
Да, можно попробовать и дальше ставить фишки в одну строку с теми, куда только что ставил Гензель! А как это красиво оформить и понять? Может, посмотрим в сторону разбиений?
Подсказка 4
Например, разбиение 1х2! Как только Гензель займёт одну из клеток такого прямоугольника, Гретель закрывает вторую, каждым ходом забирая на 4 очка больше брата. Теперь можем найти миниальное количество очков, что она точно заберёт. Мы знаем, сколько очков они заработают на двоих и насколько больше очков Гретель получает каждым ходом. Остаётся только найти их общий отрыв по очкам, умножив на количество ходов Гретель, и составить уравнение!
Давайте скажем, что Гензель тоже получает очки по тому же принципу, что и Гретель. В таком случае, каждая пара клеток в одной строке
даст в итоге какому-то из игроков очка, а каждая пара клеток в одном столбце —
очка. В одной строке можно найти
пар клеток, а в одном столбце —
пару. Общая сумма очков, набранных обоими игроками в конце игры, будет
равна
Приведём стратегию за Гретель, позволяющую ей каждый ход получать на очка больше, чем перед этим Гензель. Для этого разобъём
каждую строку на 4 прямоугольника
Как только Гензель ставит фишку в одну из клеток прямоугольника, Гретель тут же занимает
вторую. Столбцы, в которых находятся эти клетки, идентичны из-за стратегии Гретель, а в строке к моменту её хода находится на одну
фишку больше — ровно на ту, которую поставил Гензель.
С другой стороны, если Гензель будет каждый раз выбирать клетку, которая приносит максимальное количество очков, Гретель своим
следующим ходом сможет набрать максимум на очка больше, так как добавлением одной фишки Гензель повышает “ценность” каждой
из оставшихся клеток не более, чем на
Каждый игрок сделает ходов и, при правильной игре, Гретель наберёт на
очков больше. Зная сумму и разность двух чисел,
можно легко найти сами числа, это
и
Во всех остальных вариантах второй игрок всегда получает большее количество очков за фишку в ряду, длина которого чётна, поэтому описанная стратегия за второго игрока всегда работает.


