ИТМО 2024

Обозначим угол при вершине полученного равнобедренного треугольника за Назовем новые точки центр вписанной окружности — Тогда — равные прямоугольные треугольники, в частности, углы при вершине у них равны Кроме того, центр описанной окружности треугольника — также точка Если бы все эти 3 угла откладывались в одну сторону (по или против часовой стрелки), получился бы треугольник, подобный исходному. Однако есть еще случай, когда два угла отложены в одну сторону, допустим, по часовой стрелке, а третий, — в другую.

Заметим, что исходный треугольник получается из двойственного таким же преобразованием, только все повороты точек осуществляются в другую сторону. Рассмотрим углы, которые лучи образуют с лучом Если угол откладывается по часовой стрелке, будем считать его с минусом, иначе — с плюсом. Тогда образует угол Пусть лучи и образуют с углы и Тогда и образуют с углы и Тогда мы можем выразить углы С учетом направления, получаем Изменился ли порядок точке на окружности у нового треугольника по сравнению со старым? Это так, если то есть или Учитывая принятое нами расположение точек на окружности,

Значит, положение точек меняется, если сумма двух соответствующих углов треугольника больше При этом в наших условиях ни один из углов сам по себе не больше значит, точка не может «перепрыгнуть» через точки и сразу. В случае, если порядок точек остался неизменным, углы исходного треугольника — это половины посчитанных нами и а также угла

Значения углов исходного треугольника — и Но и — это и есть углы какие-то углы треугольника а — третий угол, уменьшенный на Так как — угол при вершине равнобедренного треугольника получим 3 подслучая:

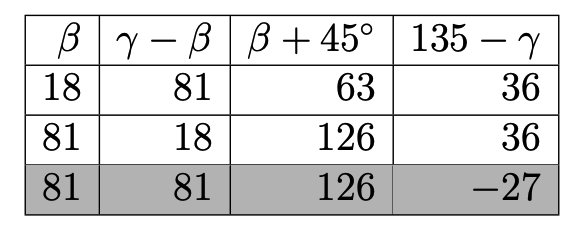
Вычисляем следующие значения:

Получаем такие тройки значений углов:

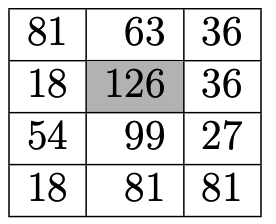
Наибольший угол равен это и будет ответом.