ИТМО 2024

Производная многочлена равна

Видно, что 36 корней этого выражения являются корнями многочлена или его производной (могут быть одновременно корнями и многочлена, и производной).

По теореме Ролля между каждыми двумя корнями многочлена находится корень производной, не являющийся при этом корнем многочлена. Поэтому если у многочлена хотя бы 19 корней, то у его производной хотя бы 18 отличных от этих 19 корней. Так что суммарно уже хотя бы различных корней, а это уже больше 36.

_________________________________________________________________________________________________________________________________________________________________________________

Лемма (доказывать на олимпиаде не требовалось): Если число является корнем многочлена кратности то для производной число является корнем кратности

______________________________________________________________________________________________________________________________________________________

Пример на 18 корней строится так: рассмотрим многочлен

У него и у его производной 18 корней, но есть общий (только общий по лемме, оставшиеся 17 корней находятся между корнями по теореме Ролля). Тогда у 35 корней.

Но при достаточно маленьком (можно взять конкретное ) многочлен будет иметь так же 18 корней и такую же производную, но будет иметь уже 36 корней за счёт того, что перестанеть являться корнем .

У числа шестнадцать делителей и все они являются делителями числа . Если делится на , то к этим делителям добавляются ещё числа 16,48 и 80 , то есть 120 — это уже как минимум девятнадцатый делитель.

Если делится на , то к исходным шестнадцати делителям добавляются 9,18 и 45 . Если делится на , то к исходным шестнадцати делителям добавляются 25,50 и 75.

Значит, делится на какое-то простое число , кроме 2,3 и 5 . Если это число не превосходит 40 , то числа и являются делителями , меньшими 120 , и мы опять получаем слишком много делителей. Значит, хотя бы 41 , то есть . Заметим, что это число нас как раз устраивает.

Вырежем из нашего куба куб и разобьём его на 64 куба .

Предположим, что в каждом кубике закрашено не более трёх ячеек, то есть всего не более 192.

В исходном кубе после этого остались кубики на трёх гранях, имеющих общую вершину. Рассмотрим 64 клетки на одной из этих граней, которые не лежат ни на какой из двух других. Они разбиваются на 16 квадратов , в каждом из которых не более трёх закрашенных ячеек. Итого на трёх гранях получаем не более .

У нас остались не рассмотренными 25 ячеек, образующих три ребра исходного куба, сходящиеся в одной вершине. Среди них закрашены не более 24, так как общая ячейка трёх этих рёбер и три её соседних лежат в одном кубике , значит, среди этих четырёх ячеек не более трёх закрашенных.

Таким образом, мы получаем максимум закрашенных ячеек, что противоречит условию задачи. Значит, наше предположение было неверно.

После замены

условие, что исходные числа не меньше превращается в

а условие на произведение превращается в

Искомое выражение по формуле перехода и свойствам логарифмов равно

Воспользуемся методом Штурма. Пусть имеется какое-то значение искомого выражения при удовлетворяющих условиям выше (не умаляя общности, переменные можно переименовать для упорядочивания). Заменим два числа на числа с такой же суммой и не меньшей разностью Тогда в искомом выражении сумма дробей

не изменится, а сумма дробей

и аналогичная ей (с точностью до перестановки ) сумма дробей

не уменьшатся, так как после приведения к общему знаменателю у получившейся дроби числитель увеличивается при увеличении а знаменатель уменьшается при увеличении

Такими преобразованиями можно превратить три наименьших числа из в единицу, а наибольшее — в при этом наше выражение будет увеличиваться (точнее, заведомо не уменьшаться). Итак, максимальное значение выражения равно

Радиусы и равны друг другу и высоте трапеции. Из условия про пересечение лучей следует, что — меньшее основание.

Проведём вторую касательную к вписанной окружности треугольника параллельную основаниям трапеции. Обозначим за и точки пересечения этой касательной с отрезками и — трапеция.

Точки касания окружностей и оснований трапеции образуют квадрат со стороной . Если вырезать этот квадрат из трапеции и склеить оставшиеся части между собой, получится трапеция, равная .

Более точно, обозначим точки касания окружностей и с основаниями трапеции : пусть и лежат на ( ближе к ), и лежат на ( ближе к ). Кроме того, пусть — точки касания вписанной окружности с соответственно. Кроме того, пусть и — точки касания окружностей и с боковыми сторонами трапеции, и — центры окружностей и вписанной окружности треугольника .

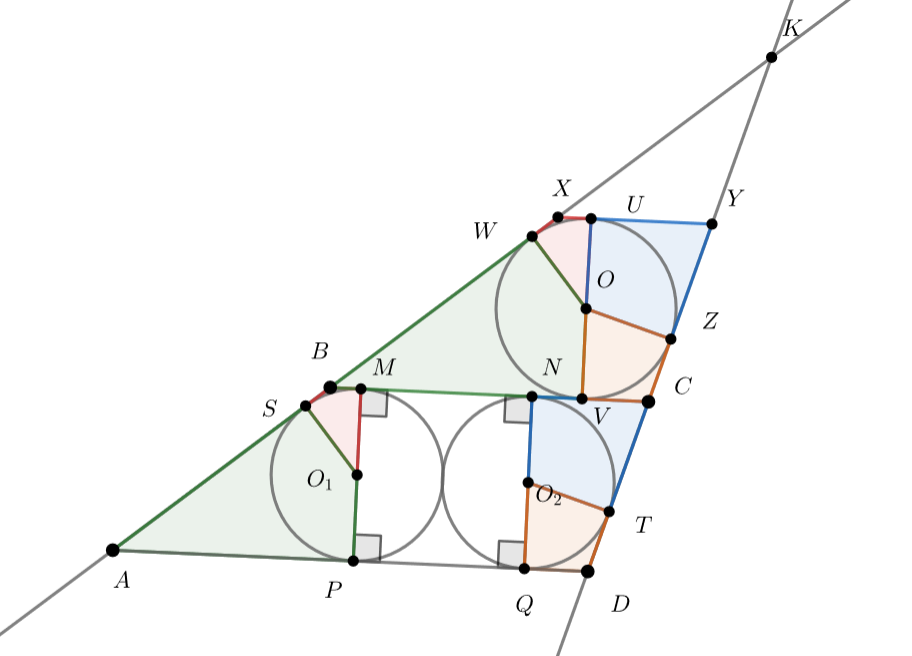
Рассмотрим четырёхугольники и

как соответственные. , прямые.

Значит оставшиеся углы, и также равны. Значит, треугольники и равны. Следовательно, треугольники и также равны, а значит четырёхугольники и равны. Аналогично

Значит,

Пусть — длина высоты треугольника , проведённой из точки . Тогда длина высоты треугольника , проведённой из точки равна . Значит, коэффициент подобия треугольников и с одной стороны равен , а с другой , откуда . Значит, площадь треугольника равна

Пусть — центр описанной окружности треугольника , лежащий на — центр сферы. Очевидно, — середина . Так как точки и лежат на сфере, перпендикулярно плоскости . С другой стороны, и — это одна и та же прямая, а перпендикулярна плоскости . Значит, плоскости и параллельны, а тетраэдры и подобны.

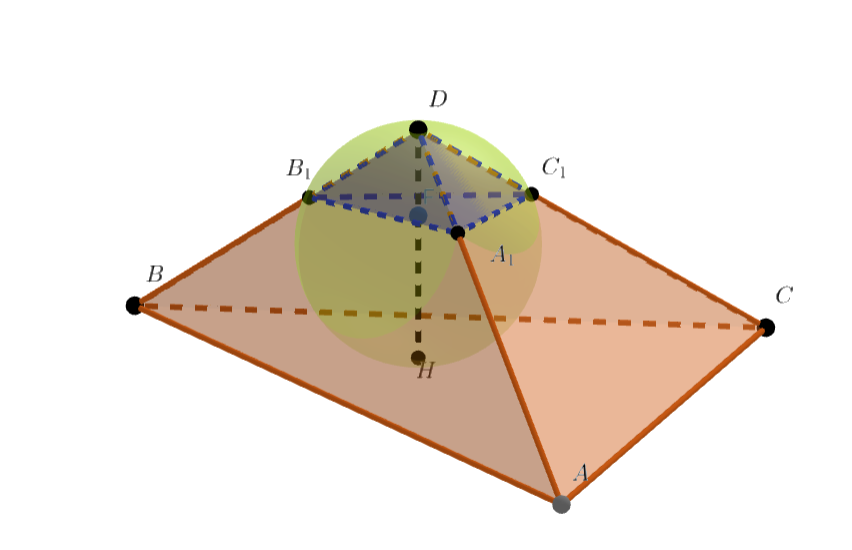
Пусть — длина , то есть высота маленького тетраэдра. Высота большого тетраэдра равна , а коэффициент их подобия .

- прямоугольный треугольник с прямым углом , значит, радиус описанной окружности треугольника , то есть , равен

Как известно, среди всех треугольников, вписанных в данную окружность, наибольшую площадь имеет равносторонний. Для окружности радиуса эта площадь составляет

Значит, объемы тетраэдров составляют

и

а их произведение равно

Чтобы максимизировать эту величину, достаточно максимизировать

В первой точке достигается минимум, равный нулю, а во второй — максимум. Подставив в формулу для объёма, получим

Рассмотрим некоторого человека, назовём его . Пусть его шляпа изначально оказалась у какого-то , шляпа оказалась у , и т.д. Рассмотренный нами процесс нумерации рано или поздно закончится тем, что для какого-то его шляпа окажется у какого-то , который был уже нами пронумерован ранее. При этом это может быть только , т.к. про всех остальных мы уже знаем, откуда взялись находящиеся у них шляпы.

Значит, шляпа в начале представления оказалась у и мы получили так называемый цикл из человек. Для удобства будем считать, что и т.д., чтобы иметь возможность говорить, что каждый человек с номером передал свою шляпу человеку с номером (то есть, мы на самом деле нумеруем людей остатками (классами вычетов) при делении на ).

После того, как джентльмены передадут свои шляпы, шляпа окажется у того, у кого раньше была шляпа , то есть у , шляпа окажется у и т.д. Шляпа каждого окажется у . После второй передачи шляпа каждого окажется у и т.д. Через минут шляпа окажется у .

Если это тот же человек, что и , разность их номеров, то есть , должна делится на . Значит, шляпа может вернуться к исходном владельцу, только если количество человек в цикле является степенью двойки. При этом фокусник хочет, чтобы был цикл как можно большей длины.

Самая большая степень двойки, не превосходящая 100, это . Фокусник в начале должен разбить пришедших на представление на циклы, длины одного из которых равна 64, а длины остальных — меньшие степени двойки, не важно какие. Тогда через 6 минут все шляпы окажутся у своих настоящих владельцев (у некоторых они окажутся раньше, но в этот момент это впервые произойдёт для всех сразу).

Перепишем рекуррентную формулу:

Записав её для вместо получим

откуда

Поскольку то

Значит,

Посчитаем, чему равна сумма первых членов. Мы можем симметрично расписать члены арифметической прогрессии, тогда сумма нечётного числа членов равна количеству членов, умноженному на средний член:

аналогично для Поскольку суммы прогрессий равны,

Пусть — разность прогрессии тогда

Пусть — разность прогрессии тогда с другой стороны,

Значит,

Так как и взаимно просты, делится на а делится на Наименьшее возможное значение равно а значит, наименьшее возможное значение

Поскольку мы можем сократить равенство на Получим

Обозначим тогда где и взаимно просты. Получим

Сократим на

Значит, делится на При этом и взаимно просты друг с другом, а значит, и Значит, делится на

Пусть Тогда

Отсюда

Число 67 — простое, значит,

Перебрав все варианты от 1 до 8, получим и или наоборот. Также откуда или наоборот.

Лучи и пересекаются в точке значит, что и — боковые стороны, — меньшее основание, а — большее. Вписанная окружность трапеции является одновременно вписанной окружностью треугольника и вневписанной окружностью треугольника

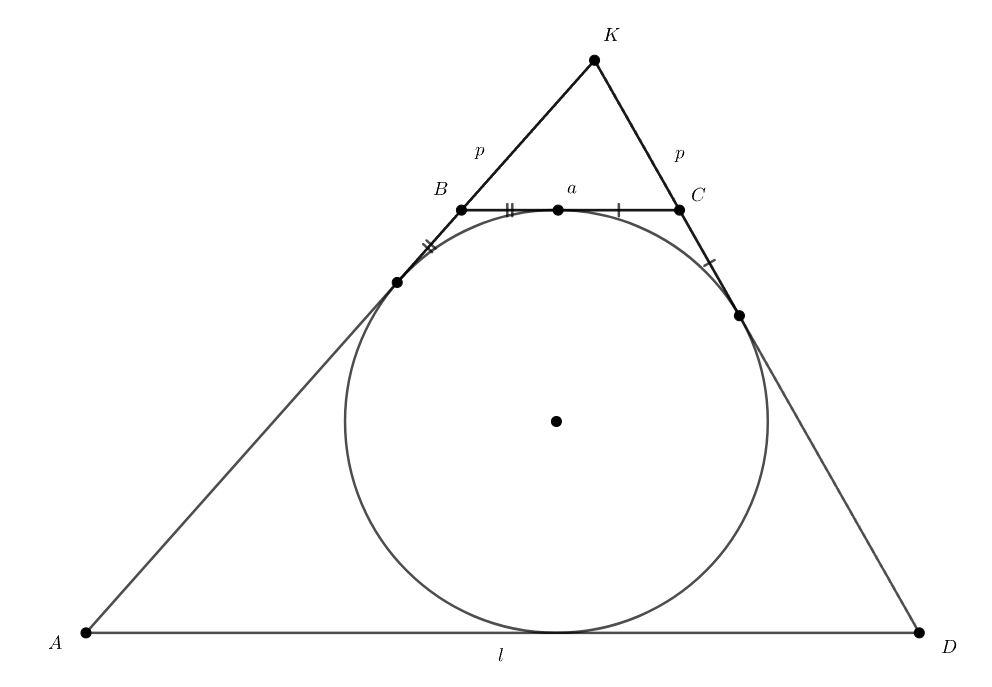
В подобных треугольниках соответствующие элементы относятся как коэффициент подобия. В частности, это верно для отрезков касательных, проведённых к вписанным окружностям из точки В большом треугольнике эти отрезки равны так как вписанная окружность трапеции является вневписанной окружностью треугольника В треугольнике эти отрезки равны где

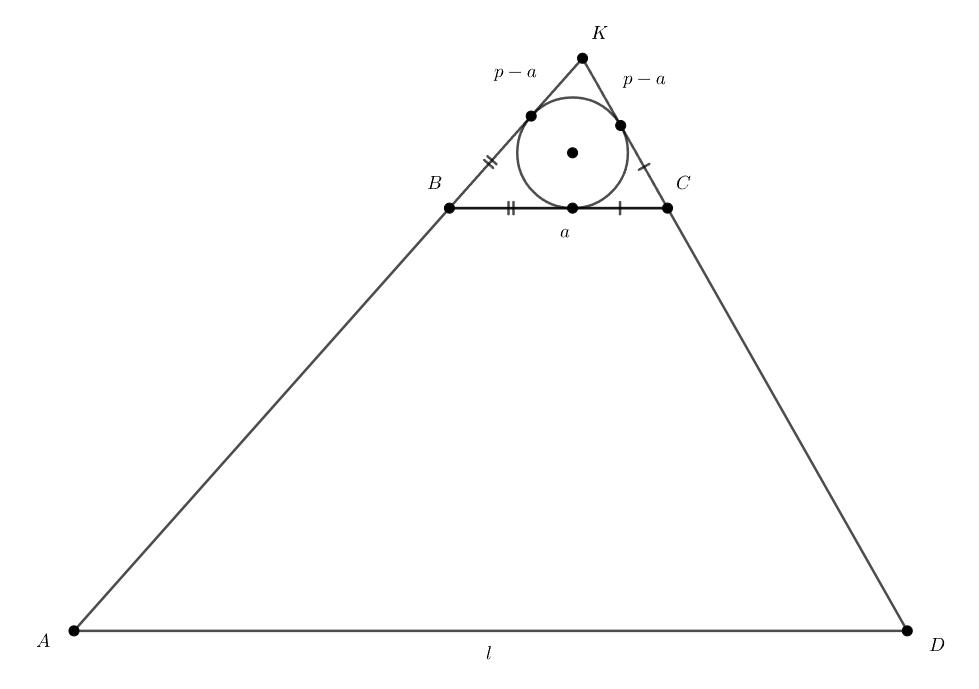
Коэффициент подобия равен откуда

Преобразуя это равенство, получаем

Число частей, на которые разбивается -угольник, равно В один треугольник входит не более двух сторон -угольника, значит, число частей, содержащих эти стороны, не менее Оставшиеся части могут не содержать сторону -угольника.

В качестве примера отрезаем по две стороны каждым новым треугольником.

Обозначим угол при вершине полученного равнобедренного треугольника за Назовем новые точки центр вписанной окружности — Тогда — равные прямоугольные треугольники, в частности, углы при вершине у них равны Кроме того, центр описанной окружности треугольника — также точка Если бы все эти 3 угла откладывались в одну сторону (по или против часовой стрелки), получился бы треугольник, подобный исходному. Однако есть еще случай, когда два угла отложены в одну сторону, допустим, по часовой стрелке, а третий, — в другую.

Заметим, что исходный треугольник получается из двойственного таким же преобразованием, только все повороты точек осуществляются в другую сторону. Рассмотрим углы, которые лучи образуют с лучом Если угол откладывается по часовой стрелке, будем считать его с минусом, иначе — с плюсом. Тогда образует угол Пусть лучи и образуют с углы и Тогда и образуют с углы и Тогда мы можем выразить углы С учетом направления, получаем Изменился ли порядок точке на окружности у нового треугольника по сравнению со старым? Это так, если то есть или Учитывая принятое нами расположение точек на окружности,

Значит, положение точек меняется, если сумма двух соответствующих углов треугольника больше При этом в наших условиях ни один из углов сам по себе не больше значит, точка не может «перепрыгнуть» через точки и сразу. В случае, если порядок точек остался неизменным, углы исходного треугольника — это половины посчитанных нами и а также угла

Значения углов исходного треугольника — и Но и — это и есть углы какие-то углы треугольника а — третий угол, уменьшенный на Так как — угол при вершине равнобедренного треугольника получим 3 подслучая:

Вычисляем следующие значения:

Получаем такие тройки значений углов:

Наибольший угол равен это и будет ответом.

Автор задачи забыл добавить условие, что в стране нет «треугольников», то есть троек городов, попарно соединённых друг с другом. Без этого условия утверждение задачи неверно.

Рассмотрим множество из города соединим в нём все города со всеми, кроме каких-то городов и Рассмотрим ещё одно множество из города соединим в нём все города со всеми, кроме каких-то городов и

Среди оставшихся городов (множество ) соединим каждый город ровно с следующим образом: расставим города по кругу и соединим каждый из них с идущими по кругу после него по часовой стрелке и идущими до. Это можно сделать, так как во всех наших вариантах чётно.

Затем разрушим какие-то две дороги в этом множестве, не имеющие общего конца, и соединим четыре города, являющиеся их концами с городами и Получится картинка, в которой от любого города можно добраться до любого. При этом от города из до города из нельзя добраться менее, чем по пяти дорогам.

Действительно, из в мы можем попасть только через Для этого из мы должны попасть в или затем из него в какой-то из городов множества С другой стороны, чтобы попасть в мы должны из попасть в или а затем оттуда в Это уже четыре дороги. При этом, множество устроено так, что в нём нет общих соседей у и значит, нам нужна ещё одна дорога внутри этого множества.

Заметим, что наш многочлен возрастает. Это можно доказать, например, посчитав его производную и убедившись, что она неотрицательна.

Однако, мы докажем это не используя производную. Нам достаточно сделать это для положительных

Рассмотрим выражение

Нам надо доказать, что выражение в скобках положительно, тогда мы докажем, что

Приравняв

получим квадратное уравнение относительно с дискриминантом

Значит, всегда одного знака, а именно положительного.

Так как многочлен возрастает, для всех между и выполняются неравенства

Значит, для этих верно Аналогично для между и

А вот на промежутке многочлен принимает в том числе значение в какой-то точке, при этом для всех из этого промежутка

Рассмотрим некоторого человека, назовем его Пусть его шляпа изначально оказалась у какого-то шляпа оказалась у и т.д.. Рассмотренный нами процесс нумерации рано или поздно закончится тем, что для какого-то его шляпа окажется у какого-то который был уже нами пронумерован ранее. Заметим, что это так как про всех остальных мы уже знаем, откуда взялись находящиеся у них шляпы. Значит, шляпа в начале представления оказалась у и мы получим цикл из человек. Каждый раз каждый из участников передает свою шляпу следующему по циклу. Таким образом, шляпы в этом цикле вернутся к своим хозяевам через минуту, затем через каждые следующие следующие минут.

Таких циклов может быть несколько. Тогда если все шляпы вернутся к своим хозяевам через минут, число должно делиться на длины всех этих циклов. Таким образом, нам нужно разложить число 12 в сумму нескольких слагаемых так, чтобы их наименьшее общее кратное было максимальным. Возьмем следующее разложение:

НОК этих чисел — 60, значит, шляпы вернутся к своим хозяевам через 59 минут. Если все слагаемые являются делателями числа 24, то их НОК не больше 24. Значит, для большего НОК нужно хотя бы одно число, не являющееся делителем 24, например, 5, 7, 9, 10 или 11. Варианты, в которых все слагаемые, кроме одного, равны единице, нам не нужны. Переберем оставшиеся варианты для слагаемых, больших 5:

• НОК
• НОК
• НОК
• НОК Для вариантов и НОК, очевидно, еще меньше.
• НОК

Осталось рассмотреть варианты с 5. Если все остальные делители не больше 6, НОК не больше, чем 60, а вариант с 7 мы уже разобрали. Значит, ответ — 59.