ИТМО 2024
Ошибка.
Попробуйте повторить позже
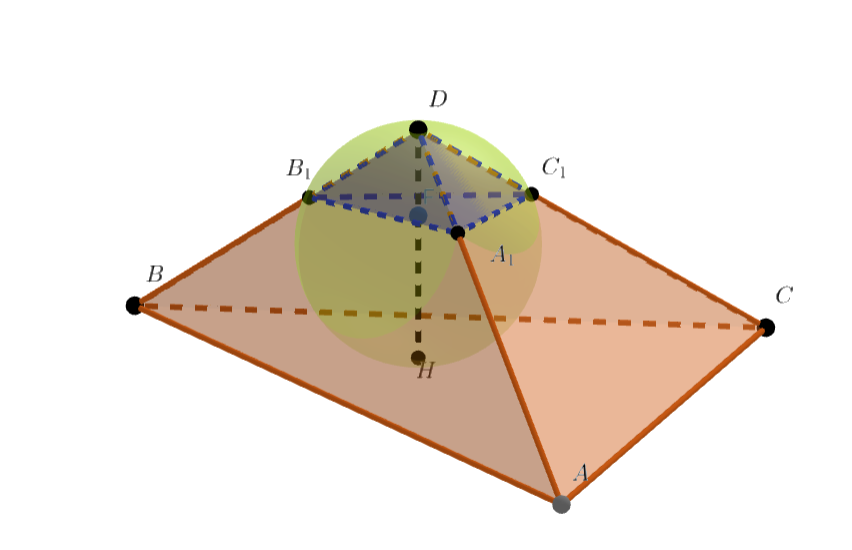
Сфера касается основания
тетраэдра
в точке
и проходит через вершину
. Рёбра
и
эта сфера
пересекает в точках
и
. Центр описанной окружности треугольника
лежит на отрезке
. Радиус сферы
равен
.
Пусть - объём тетраэдра
, а
- объём тетраэдра
. Какое наибольшее значение может принимать
Источники:
Подсказка 1
Какие фигуры и точки стоит рассмотреть первым делом?
Подсказка 2
Обратите внимание на центр сферы (обозначим его O). Где он находится?
Подсказка 3
На самом деле, это середина DH! Попробуйте посмотреть на плоскость A₁B₁C₁.
Подсказка 4
Заметим, что прямая OH₁ перпендикулярна плоскости A₁B₁C₁. Что еще можно сказать про OH₁?
Подсказка 5
Она перпендикулярна плоскости ABC, следовательно, эти плоскости параллельны. Какое еще вывод можно сделать?
Подсказка 6
Тетраэдры ABCD и A₁B₁C₁D подобны! Обозначим за h высоту малого тетраэдра DH₁. Найдите высоту большого тетраэдра и коэффициент подобия.
Подсказка 7
Посмотрите на треугольник OH₁A. Что можно найти благодаря ему?
Подсказка 8
Вычислите радиус описанной окружности треугольника A₁B₁C₁. Как с ее помощью можно максимизировать объем?
Подсказка 9
У какого из треугольников, вписанных в одну окружность, будет наибольшая площадь?
Подсказка 10
У равностороннего!
Пусть — центр описанной окружности треугольника
, лежащий на
— центр сферы. Очевидно,
— середина
.
Так как точки
и
лежат на сфере,
перпендикулярно плоскости
. С другой стороны,
и
— это одна и
та же прямая, а
перпендикулярна плоскости
. Значит, плоскости
и
параллельны, а тетраэдры
и
подобны.
Пусть — длина
, то есть высота маленького тетраэдра. Высота большого тетраэдра равна
, а коэффициент их подобия
.
- прямоугольный треугольник с прямым углом
, значит, радиус описанной окружности
треугольника
, то есть
, равен
Как известно, среди всех треугольников, вписанных в данную окружность, наибольшую площадь имеет равносторонний. Для окружности
радиуса эта площадь составляет
Значит, объемы тетраэдров составляют
и
а их произведение равно
Чтобы максимизировать эту величину, достаточно максимизировать
В первой точке достигается минимум, равный нулю, а во второй — максимум. Подставив в формулу для объёма,
получим
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




