Тема Бельчонок - задания по годам

Бельчонок 2022

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела бельчонок - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#58323

На продолжении за точку $C$ стороны $BC$ равностороннего треугольника $ABC$ выбрана точка $M$ , через неё проведена прямая, параллельная $AC$ . Эта прямая пересекает продолжение стороны $AB$ в точке $N$ . Медианы треугольника $BNM$ пересекаются в точке $O$ . Точка $D$ — середина $AM$ . Найдите углы треугольника $ODC.$

Источники: Бельчонок-2022, 11.2 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Проведем отрезок АК такой, чтобы АК было параллельно СМ! Заметим, что тогда АКМС это параллелограмм.

Подсказка 2

Давайте заметим, что треугольник BNM правильный, откуда для его центра O: OM = ON ! Тогда мы можем попробовать отметить равные углы и равные отрезки на нашей картинке (их тут много!)

Подсказка 3

Попробуйте доказать, что треугольники KON и COM равны, и, используя, что D - точка пересечения диагоналей параллелограмма, подсчитать углы в треугольнике!

Показать ответ и решение

$PIC$

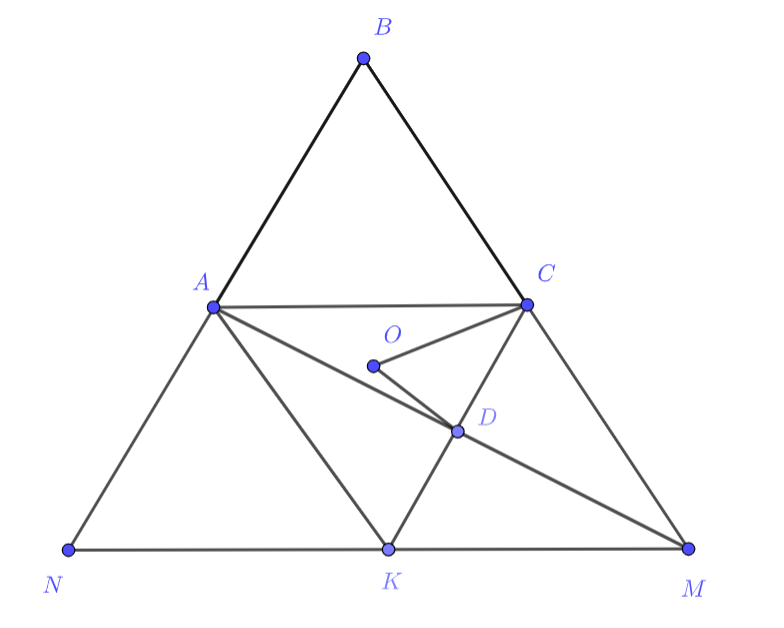
Рассмотрим $K ∈NM, AK ∥CM$ , откуда $AKMC$ — параллелограмм. Заметим, что

В $△AKN :∠N = 60∘,AK ∥BC$ , откуда он равносторонний и $NK = NA =MC$ (в силу симметрии).
Треугольник $BNM$ правильный, откуда для его центра $O$ : $OM = ON$ .
Аналогично предыдущему $∠KNO = ∠N2-= ∠M2-= ∠CMO =30∘$ .

Отсюда по двум сторонам и углу между ними $△KON =△COM$ , тогда $OK = OC$ . Поскольку $D$ является точкой пересечения диагоналей параллелограмма, то $KD =DC$ и $OD$ является медианой равнобедренного $△KOC$ . Отсюда $∘ ∠ODC = 90$ и

∠KOC ∠KOM + ∠MOC ∠KOM +∠KON ∠NOM ∠DOC = --2--= ------2------ = ------2------= ---2-- =60∘

снова пользуясь правильностью $△BNM$ . В итоге получаем $∠OCD = 180∘− ∠DOC − ∠CDO = 30∘$ .

Ответ:

$90∘,60∘,30∘$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#74648

Борис раскладывает 8 белых и 8 чёрных шариков по двум коробкам. Настя наугад выбирает коробку, а потом не глядя берёт из неё шарик. Может ли Борис так разложить шарики по двум коробкам, чтобы вероятность вынуть белый шарик была больше $2 3?$

Источники: Бельчонок-2022, 11.1 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Попробуем придумать несложный пример. Как сделать так, чтобы Настя с большой вероятностью вынула белый шарик, выбирая лишь одну из двух коробок?

Подсказка 2

Положим один белый шарик в одну из коробок!

Показать ответ и решение

Борис положит в первую коробку 1 белый шарик, а во вторую все остальные. Тогда вероятность вынуть белый шарик равна

1 1 7 22 2 2 + 2 ⋅15-= 30 > 3

Ответ: да

Ошибка.
Попробуйте повторить позже

Задача 3#74649

На отрезке $[2;5]$ выбрали три разные точки, для каждой точки перемножили расстояния до двух других точек, получили положительные числа $a,b,c.$ Докажите, что

1 1 1 8 a +b + c ≥ 9

Источники: Бельчонок-2022, 11.3 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Какой-то странный у нас отрезок - [2;5]. Быть может, мы сможем его как-то улучшить? Попробуем также расписать выражение из условия с помощью выбранных на отрезке чисел и как-нибудь оценить.

Подсказка 2

[2;5] можно сдвинуть до отрезка [0;3]. Попробуем выразить знаменатель каждой дроби через x, y, z. Теперь можем оценить сумму дробей, увеличив знаменатели. Но как именно?

Подсказка 3

Попробуем "сдвинуть" границы нашего отрезка: x к нулю, а z к 3. Уменьшатся ли знаменатели?

Показать доказательство

Переместим отрезок в точку $0,$ то есть будем рассматривать отрезок $[0;3].$ Обозначим взятые точки $0≤ x< y < z ≤3.$ Тогда, т.к. $− x ≤0,z ≤ 3,$

1 1 1 1 1 1 a +-b + c = (y−-x)(z−-x) + (y−-x)(z−-y) + (z− y)(z-− x)

----1-----+ -----1---- +-----1---- ≥ -1-+ ---1-- +---1--- (y − x)(z − x) (y− x)(z− y) (z− y)(z− x) y⋅3 y(3− y) (3− y)⋅3

При замене $− x$ на 0, а $z$ на 3 все знаменатели увеличились, а обратные им величины уменьшились.

1 (1+ ---3-- +--1-- )= 3−-y+-3+-y= --2--- 3 y y(3− y) (3− y) 3y(3− y) y(3 − y)

Тогда

2 8 y(3-− y) ≥ 9 ⇔ (2y− 3)2 ≥0

Ошибка.
Попробуйте повторить позже

Задача 4#74652

Найдите все натуральные числа $a,$ для которых число

a+1 +√a5-+2a2+-1 -----a2+-1------

также является натуральным.

Источники: Бельчонок-2022, 11.4 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Мы хотим сделать так, чтобы числитель делился на знаменатель. Попробуем сделать замену а+1=b, так же заменим и корень. Что получится?

Подсказка 3

Может ли -а-1 быть сравнимо с нулем по модулю a^2+1?

Показать ответ и решение

Обозначим $a+ 1= b,√a5-+2a2+-1= c$ . В числителе записано

c2-− b2 c+ b= c− b

На $a2+ 1$ должно делиться

c2− b2 = a5+ 2a2+ 1− (a +1)2 = a5+a2− 2a≡a2+1 −a − 1

При $a> 1$ модуль остатка меньше $2 a +1,$ поэтому остаток не может делиться на $2 a + 1$ ни при каком $a> 1.$ Уравнению удовлетворяет единственное значение $a= 1.$

Ответ: 1

Ошибка.
Попробуйте повторить позже

Задача 5#74657

Найдите целую часть числа

---1--- ---1--- -----1---- √1 +√2-+ √3+ √4 +⋅⋅⋅+√623-+√624

Источники: Бельчонок-2022, 11.5 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Гораздо удобнее работать с целочисленными знаменателями-> что нужно сделать, чтобы они стали именно такими? Попробуем оценить число А другим число так, чтобы нам было удобно оценивать их разность двумя способами. Тогда мы сможем прийти к оценке числа А!

Подсказка 3

А+В=24(почему?). Теперь мы можем оценить их разность, группируя соответствующие слагаемые.

Подсказка 4

Их разность меньше 1, а сумма равна 24. Осталось ли ль сделать соответствующие выводы)

Показать ответ и решение

Обозначим

--1---- ---1--- ----1----- A = √1+ √2 +√3-+ √4 + ⋅⋅⋅+ √623+ √624

Возьмём число

B = √--1√--+ √-1-√-+ ⋅⋅⋅+ √---1-√--- 2+ 3 4+ 5 624+ 625

Число слагаемых одинаково, каждое слагаемое в $A$ больше соответствующего слагаемого в $B,$ поэтому $A > B.$ Избавимся от иррациональности в знаменателях:

A= √2-− √1-+√4 − √3+ ⋅⋅⋅+ √624− √623

B =√3-− √2-+ √5− √4+ ⋅⋅⋅+ √625− √624

Очевидно, $√ --- √- A+ B = 625 − 1 =24.$ Оценим $A − B.$

( ) ( A− B =√--1-√-− √--1-√-− √--1√-- − ⋅⋅⋅− √---1-√---− 1+ 2 2+ 3 3 + 4 622+ 623

− √---1-√---)− √---1-√---< √--1√--< 1 623+ 624 624+ 625 1+ 2

Подставим $B = 24 − A :$

A− 24+ A< 1,

отсюда $A < 12,5.$ Но $A > B,$ значит, $A >12.$ Следовательно, целая часть числа $A$ равна 12.

Ответ: 12

Ошибка.
Попробуйте повторить позже

Задача 6#76734

Найдите все пары $(x;y)$ натуральных чисел, для которых оба числа $x2+8y;y2− 8x$ являются точными квадратами.

Источники: Бельчонок - 2022, 11.5 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Давайте внимательно посмотрим на наши выражения. Нельзя ли сразу угадать какую-то пару чисел, удовлетворяющую условиям задачи. Пусть x равен какому-то натуральному n. Тогда какой должен быть y, чтобы первое выражение было квадратом?

Подсказка 2

Верно, тогда y=n+2. Можно проверить, что условие задачи выполняется. Что же делать теперь? Ведь y может быть больше или меньше x+2. Какую идею тогда здесь можно применить для дальнейшей оценки наших выражений, чтобы перебирать другие варианты было проще?

Подсказка 3

Да, можно попробовать зажать наши числа между квадратами. Если y < x+2, то первое выражение будет находиться между x² и (x+4)², и остаётся только вариант для (x+2)² = x² + 8y из-за чётности. Аналогично рассматривается, если y > x+2. Тут уже второе число зажимается между y² и (y-4)². Осталось только технически это всё реализовать и найти оставшиеся решения. Победа!

Показать ответ и решение

Легко проверить, что пары вида $(n;n +2)$ , где n – натуральное число, удовлетворяют условию задачи. Пусть $(x;y)$ – любая другая пара, удовлетворяющая условию задачи. Рассмотрим два случая.

1) Пусть сначала $y < x+ 2$ . Тогда $2 2 2 2 x <x + 8y < x + 8(x+ 2)= (x+ 4)$ , откуда $2 2 x + 8y =(x+ k)$ , где $k ∈{1;2;3}$ . Очевидно, возможен лишь случай $k= 2$ (по чётности), и тогда $x= 2y − 1$ .

Осталось выяснить, при каких натуральных $y$ число $2 2 y − 8x= y − 16y+ 8$ будет точным квадратом. Пусть $2 2 y − 16y+ 8= a$ , тогда $√-----2 y =8± 56+ a$ . Число под корнем должно быть точным квадратом: $2 2 56+ a = c$ , т. е. $2 2 c− a = 56$ .

Разложим $56$ на множители и рассмотрим системы. Учитывая, что $c− a$ и $c+ a$ имеют одинаковую чётность, отбросим лишние, останутся системы:

{ c− a = 4 c+ a = 14

{ c− a = 2 c+ a = 28

откуда $c= 9,a= 5$ или $c= 15$ , $a= 13$ .

При $a= 5$ значение $y = 8± √56+25$ и подходит $y = 8+9 =17$ . При $a= 13$ значение $y = 8± √56+-169$ и подойдет $y =8+ 15= 23$ . Поскольку $x= 2y− 1$ , получаем пары $(45;23)$ и $(33;17)$ .

2) Пусть теперь $y > x+ 2$ , т. е. $x <y − 2$ . Здесь $y > 4$ , и мы имеем $(y− 4)2 = y2− 8(y− 2)<y2− 8x< y2$ . Значит, $y2− 8x= (y − k)2$ , где $k ∈{1;2;3}$ . Опять возможен только случай $k= 2$ (по чётности), так что $y = 2x +1$ .

Пусть $x2 +16x+ 8= b2$ , тогда $x= −8± √56+-b2$ . Выше показано, что число под корнем является точным квадратом только при $b= 5$ или $b= 13$ . Тогда $x =1$ или $x =7$ . Получаем пары $(1;3)$ и $(7;15)$ , первая из которых входит в множество $(n;n+ 2)$ .

Ответ:

$(7;15),(33;17),(45;23),(n;n+ 2),n∈ ℕ$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#77812

Найдите для всех натуральных $n >1$ положительные решения системы

{ x +2x + ⋅⋅⋅+ nx = 3 11+ -21-+⋅⋅⋅+-1n =3 x1 2x2 nxn

Источники: Бельчонок - 2022, 11.2 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Слишком много переменных, и еще они умножаются на коэффициенты какие-то. Попробуем вместо переменных x_i ввести y_i таким образом, чтобы нам стало приятнее жить. И для y_i уже можно что-то заметить.

Подсказка 2

Думаю, Вы догадались, что замена нужна такая: i*x_i = y_i. Тогда обращаем внимания, что во втором уравнении слагаемые - обратные величины к слагаемым первого. Что мы знаем про сумму положительного числа и его обратной величины?

Подсказка 3

Как с помощью этого неравенства мы можем отбросить из рассмотрения много случаев?

Подсказка 4

На этом этапе вам остается рассмотреть отдельно n = 2 и n = 3 и решить задачу для них. Здесь уже нет ничего сложного!!

Показать ответ и решение

Обозначим $y = kx k k$ и сложим уравнения системы:

( 1-) ( 1-) ( 1-) y1+ y1 + y2+ y2 + ...+ yn+ yn =6

Для положительных чисел справедливо неравенство об обратных: $a + 1a ≥ 2.$ Поэтому левая часть не меньше $2n,$ отсюда $n ≤3.$ При $n= 3$ каждое из слагаемых равно $2,$ отсюда $y1 =y2 = y3 = 1,$ и $x1 = 1,x2 = 12,x3 = 13.$ При $n =2$ получается система:

{ { x1+2x2 = 3, ⇒ 2x2 = 3− x1, 1x1-+ 12x2-=3. 1x1-+ 3−1x1-=3.

Решая последнее уравнение, получаем, что $3±√5 3∓√5 x1 =--2-,x2 =-4--.$

Ответ:

$x = 3±√5,x = 3∓√5 1 2 2 4$ при $n= 2;$

$1 1 x1 =1,x2 = 2,x3 = 3$ при $n= 3;$

при других $n$ решений не существует.

Ошибка.
Попробуйте повторить позже

Задача 8#77816

Каким числом способов можно разложить 30 яблок в 3 корзинки так, чтобы в первой корзинке лежало меньше яблок, чем во второй, во второй меньше, чем в третьей, и пустых корзинок не было?

Источники: Бельчонок - 2022, 11 (см. dovuz.sfu-kras.ru)

Показать ответ и решение

Рассмотрим уравнение

a+ b+ c= 30.

Расставим $30$ единиц в ряд, выберем два промежутка между единицами и поставим в них по чёрточке. Число единиц слева от первой чёрточки равно $a$ (число яблок в первой корзине), справа от второй равно $c$ (число яблок в третьей корзине). Число способов выбрать два промежутка равно $29⋅28-= 406. 2$

Надо вычесть из этого числа количество случаев, когда среди чисел $a,b,c$ есть равные.

Пусть $a= b$ . Тогда $2a+ c= 30$ , это уравнение имеет $14$ ненулевых решений ( $2a$ чётное и может изменяться от $2$ до $28$ ). Аналогично будет по $14$ случаев, когда $b= c$ или $a= c.$

Итак, $406− 3⋅14 =364$ . Случай $a= b= c$ посчитан один раз в общем числе способов и три раза вычтен, а надо его исключить всего один раз, поэтому требуется прибавить $2.$

Число $364+ 2= 366$ равно числу упорядоченных троек различных $a,b,c$ . Но нужен порядок $a< b< c$ , поэтому разделим на число перестановок трёх элементов: $366- 6 = 61.$

Ответ: 61

Ошибка.
Попробуйте повторить позже

Задача 9#82776

B прямоугольнике $ABCD$ сторона $BC =3.$ На стороне $AB$ отмечена её середина — точка $P.$ Из точки $C$ опущен перпендикуляр $CQ$ на $DP.$ Найдите длину $BQ.$

Источники: Бельчонок - 2022, 11 (см. dovuz.sfu-kras.ru)

Подсказки к задаче

Подсказка 1

Видим, что у нас отмечена середина отрезка, а точку P и DP хотелось бы как-нибудь в целом получше связать с картинкой. Какое тогда дополнительное построение хорошо бы сделать?

Подсказка 2

Верно, давайте продлим DP до пересечения с продолжением BC в точке M. Что тогда можно сказать про прямоугольные треугольники PAD и BPM?

Подсказка 3

Да, они ведь равны по катету и острому углу. То есть мы получаем, что MB=AD=BC. Но нам нужен отрезок BQ. Заметим, что у нас получился ещё один прямоугольный треугольник. Что можно сказать про BQ в нём?

Подсказка 4

Верно, BQ является медианой в нём. Осталось только вспомнить, свойство медианы в прямоугольном треугольнике, и победа!

Показать ответ и решение

Продлим $CB$ и $DP$ до пересечения, пусть $M$ — это точка их пересечения.

$PIC$

Прямоугольные треугольники $MBP$ и $DAP$ равны, так как имеют равные катеты, $BP = AP,$ потому что $P$ — середина, и равные острые углы, $∠MP B = ∠AP D,$ как вертикальные. Значит, $MB = AD = BC.$ Таким образом, $BQ$ — медиана прямоугольного треугольника $MQC,$ и равна половине гипотенузе $MC,$ то есть $3.$

Ответ:

$3$

Ошибка.
Попробуйте повторить позже

Задача 10#105885

Для отбора на соревнования борец Владимир должен был провести три схватки и одержать подряд хотя бы две победы. Его соперниками были Андрей (А) и Борис (Б). Владимир мог выбрать схему встреч: АБА или БАБ. Вероятность Владимира потерпеть поражение в одной схватке от Бориса равна $0.3,$ а от Андрея $0.4;$ вероятности постоянны. При какой схеме вероятность отобраться на соревнования больше, и чему равна эта вероятность?

Подсказки к задаче

Подсказка 1

Раз у нас две независимые схемы, почему бы не рассмотреть их по отдельности? А на какие подслучаи, скажем, можно разбить схему БАБ?

Подсказка 2

Владимир мог победить в трёх схватках, мог только в первых двух, мог только в последних двух. Какова вероятность каждого из этих исходов? Остаётся лишь подумать, что нам делать с этими тремя вероятностями ;)

Показать ответ и решение

Пусть Владимир два раза встречается с более слабым соперником, то есть рассмотрим схему БАБ. Тогда вероятность равна

0,7⋅0,6⋅0,3 +0,7⋅0,6⋅0,7+ 0,3⋅0,6⋅0,7= 0,546

Пусть Владимир выбирает схему АБА. Тогда получим

0,6⋅0,7⋅0,4 +0,6⋅0,7⋅0,6+ 0,4⋅0,6⋅0,7= 0,588

Ответ: АБА; 0,588