Тема Межвед - задания по годам

Межвед 2022

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела межвед - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#39874

Есть $101$ клетка. Двое поочередно слева направо вписывают в эти клеточки по одной из цифр от $0$ до $9$ . Если после заполнения всех клеток сумма всех записанных цифр будет делиться на $11$ , то выиграет игрок, ходивший первым, а если не будет делиться на $11$ — то вторым. Какой из игроков выиграет при правильной своей игре и любой игре соперника? Ответ обосновать.

Источники: Межвед-2022, 11.1 (см. www.academy.fsb.ru)

Подсказки к задаче

Подсказка 1!

1) Итак, у нас ребята заполняют клетки по очереди числами, значит было здорово использовать стратегию дополнения!

Подсказка 2!

2) Да, можно всегда дополнять сумму до 9, так как цифры от 0 до 9. Попробуем играть так за второго, что у нас выйдет?

Подсказка 3!

3) Что в конце первый всегда будет ставить любое число и выиграет! Тогда попробуем играть за первого, и "передать ход" второму. То есть первый ставит какой-то х, а дальше дополняет сумму до 9. Как ему надо ходить, чтобы выиграть...?

Показать ответ и решение

Заметим, что первый игрок всегда может дописывать к предыдущему числу второго такое, что их сумма равна девяти. Тогда в парах $(2,3)...(100,101)$ сумма будет равна девяти, откуда вся сумма в клетках $2,3...101$ равна $50⋅9= 450 ≡11− 1.$ Выберем цифру в первой клетке, равной $1$ и вся сумма будет кратна $11$ при любой игре второго.

Ответ:

Первый

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#71644

Найдите количество цифр в десятичной записи числа $2100,$ если известно, что десятичная запись числа $2200$ содержит $61$ цифру.

Источники: Межвед-2022, 11.2 (см. www.academy.fsb.ru)

Подсказки к задаче

Подсказка 1

Подумайте, каким образом мы можем оценить количество разрядов в числе через степень десятки.

Подсказка 2

Если 10^n <= a < 10^(n+1), тогда число содержит в себе n+1 разрядов. Тогда для 2^200 можно записать 10^60 <= 2^200 < 10^61. Подумайте, как с помощью этого мы можем получить аналогичное неравенство для 2^100.

Подсказка 3

Возведем 10^60 <= 2^200 < 10^61 в степень 1/2.

Показать ответ и решение

Чтобы понять сколько цифр содержится в записи натурального числа $a$ , надо найти такое неотрицательное целое число $n,$ что будет справедливым неравенство $n−1 n 10 ≤a <10 .$ Такое число $n,$ очевидно, единственно. (Например, $2 3 10 ≤ 992<10 ,$ поэтому в записи числа 992 три цифры.)

Итак, надо найти такое целое неотрицательное $n,$ что $n 100 n+1 10 ≤ 2 < 10 .$ По условию $60 200 61 10 ≤ 2 < 10 .$ Возведя обе части в степень $1 2,$ получим $30 100 30+1 10 ≤ 2 < 10 2.$ Значит, в десятичной записи числа $100 2$ содержится 31 цифра.

Ответ: 31

Ошибка.
Попробуйте повторить позже

Задача 3#71645

Сократите дробь

2x6+-5x4− 3x3+-2x2− 12x−-14 4x6− 4x4− 6x3− 3x2+25x− 28

В результате сокращения степени многочленов в числителе и знаменателе должны уменьшиться.

Источники: Межвед-2022, 11.3 (см. www.academy.fsb.ru)

Подсказки к задаче

Подсказка 1

Чтобы упростить дробь, мы должны сократить числитель и знаменатель на их наибольший общий делитель. Какой алгоритм мы знаем для нахождения НОД двух чисел?

Подсказка 2

Давайте применим алгоритм Евклида для числителя и знаменателя. Найдите остаток от деления знаменателя на числитель. Это можно сделать делением «уголком».

Подсказка 3

Если сделать всё правильно, то остаток будет равен -14x⁴-7x²+49. Теперь выполните тот же алгоритм для нашего числителя и остатка и будем его продолжать, пока одно из выражений не станет равным 0, оставшееся выражение и будет НОД числителя и знаменателя. Осталось только сократить на него.

Показать ответ и решение

Найдем наибольший общий делитель многочленов, стоящих в числителе и знаменателе, используя алгоритм Евклида.

Для этого поделим с остатком знаменатель на числитель:

6 4 3 2 ( 6 4 3 2 ) 4 2 4x − 4x − 6x − 3x + 25x − 28= 2⋅ 2x +5x − 3x +2x − 12x − 14 − 14x − 7x +49

В результате деления получили остаток $− 14x4 − 7x2+ 49.$ Теперь числитель (который сейчас выступал в роли делителя) поделим (например, «уголком») на остаток:

6 4 3 2 ( 4 2 )( x2 2) 3 2x +5x − 3x + 2x − 12x− 14== −14x − 7x + 49 ⋅ − 2 − 7 + 4x + 2x− 14

Далее надо опять разделить делитель на остаток. В этот раз остаток от деления оказывается равным нулю:

( ) −14x4− 7x2 +49= − 7x ⋅4x3+ 2x− 14 2

Это означает, что многочлен $4x3+ 2x− 14$ является искомым наибольшим общим делителем числителя и знаменателя исходной дроби и он может быть «вынесен за скобки» (чтобы избежать появления дробных коэффициентов, будет удобнее использовать многочлен $2x3 +x − 7):$

Итак,

( )( ) 2x6-+5x4−-3x3-+2x2−-12x-− 14=-2x3+-x−-7-⋅x3+-2x+-2 4x6 − 4x4− 6x3 − 3x2+ 25x − 28 (2x3+ x− 7)⋅(2x3 − 3x+ 4)

Ответ:

$-x3+-2x-+2- 2x3− 3x+ 4$

Ошибка.
Попробуйте повторить позже

Задача 4#71647

Известно, что положительные числа $x,y,z$ удовлетворяют системе:

(| x2+ y2+ xy =529 { x2+ z2+√3xz = 441 |( 2 2 z + y = 144

Найдите значение выражения $√3xy +2yz+ xz.$

Источники: Межвед-2022, 11.5 (см. www.academy.fsb.ru)

Подсказки к задаче

Подсказка 1

Посмотрите внимательно, у нас в каждом выражении есть квадраты двух чисел и их произведение. Подумайте, на какую геометрическую теорему похожи наши выражения.

Подсказка 2

Каждое из выражений очень похоже на теорему косинусов. Как мы в таком случае можем геометрически изобразить наши уравнения?

Подсказка 3

Давайте рассмотрим треугольник ABC и точку O, расположенную внутри него. Пусть AO = y, BO = z, CO = x. В таком случае, чему равны величины углов ∠AOB, ∠AOC, ∠BOC и чему равны длины сторон треугольника ABC.

Подсказка 4

Теперь давайте рассмотрим выражение, значение которого нужно найти. Давайте перепишем его на языке сторон треугольника. Тогда сразу станет видно, что √3xy это 4 площади треугольника AOC, 2yz это 4 площади треугольника AOB, xz это 4 площади треугольника BOC. Как теперь мы можем найти значение выражения?

Подсказка 5

Значение выражения - не что иное, как 4 площади треугольника ABC. Осталось только найти его площадь, не забудьте, что мы уже нашли три его стороны.

Показать ответ и решение

Рассмотрим треугольник $ABC$ с выбранной внутри него точкой $O$ так, что

∘ ∘ ∘ AO = y,OB =z,OC =x,∠AOB = 90 ,∠AOC =120 ,∠BOC =150

$PIC$

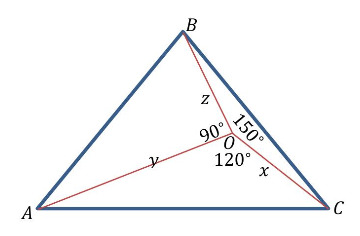
Условия системы представляют собой теорему косинусов (в т.ч. теорему Пифагора) для треугольников $AOB, AOC,BOC.$

Отсюда нетрудно понять, что $AB = 12,BC = 21,$ $AC =23.$ Теперь заметим, что

√ - 3xy+ 2yz+ xz =4SAOC + 4SAOB + 4SBOC = 4(SAOC + SAOB +SBOC )= 4SABC

Площадь треугольника $ABC$ найдем по формуле Герона:

12+ 21+ 23 √- p= ----2---- = 28, SABC = 56 5

Следовательно, $√ - 4SABC = 224 5.$

Ответ:

$224√5$

Ошибка.
Попробуйте повторить позже

Задача 5#71961

Зафиксируем 10 натуральных чисел $n ,n ,...,n 1 2 10$ и обозначим через $n$ их сумму $n= n + ⋅⋅⋅+ 1$ $n . 10$ Предположим теперь, что на доске в строчку записаны $n$ чисел $a1,...,an,$ каждое из которых равно либо 0, либо 1. Эти числа (в том порядке как они записаны) разбивают на 10 групп:

a◟1,..◝.,◜an1◞,a◟n1+1,..◝.◜,an1+n2◞,...,a◟n1+⋅⋅⋅n9◝+◜1,...,an◞ n1 n2 n10

Группу назовем ненулевой, если в ней содержится хотя бы одна 1. В результате разбиения, в зависимости от того какие числа $a,...,a 1 n$ были взяты изначально, можно получить то или иное число ненулевых групп. Нас будут интересовать такие наборы $a ,...,a , 1 n$ которые при указанном разбиении дают четное число ненулевых групп. Докажите, что число таких наборов $a1,...,an$ (где ненулевых групп будет четно) находится по формуле:

n−1 1 n n n 2 +2 ⋅(2 1 − 2)⋅(2 2 − 2)⋅...⋅(210 − 2)

Источники: Межвед-2022, 11.6 (см. www.academy.fsb.ru)

Подсказки к задаче

Подсказка 1

Нас просят найти количество наборов, подходящих под условие. То есть, нам нужно, чтобы количество не нулевых групп было четно. Но если оно четно, то оно равно 0, 2, …, 10. Значит, надо посчитать, сколько у нас вариантов для 0 групп, для 2 групп и так далее, и просуммировать. Давайте начнем с простого. Сколько у нас вариантов для 0 не нулевых групп? А для 2?

Подсказка 2

Для 0 все совсем ясно - это 1 вариант, так как подходит только 000…0. Для 2 - нам надо сначала выбрать номера групп, а потом для каждой из групп найти количество вариантов и перемножить. Как-будто просится «Цэшка», но ведь у нас количество вариантов при разных выборах номеров групп будет разным. Поэтому, нам надо суммировать по всем 1 <= i < j <= 10. А что конкретно нам надо суммировать? Сколько у нас будет вариантов выбора последовательности для группы n_i, к примеру?

Подсказка 3

Верно, нам будут подходить все варианты кроме того, когда в нашей группе стоят все нули. Поэтому для 2 групп у нас будет сумма по тому, что написано выше, величин (2^n_i - 1) * (2^n_j - 1). Меняется ли что-то при увеличении количества групп? Нет. Значит, нашли сколько всего вариантов, но пока это сумма. Значит, теперь нам надо доказать, что она сворачивается в то, что написано в условии. То есть, нам надо доказать, что сумма сумм равна некоторому выражению. А на что эти суммы похожи, если вспомнить формулу раскрытия скобок в выражении (x_1 + 1) * (x_2 + 1) * … (x_k + 1)?

Подсказка 4

Конечно, эти суммы очень напоминают формулу раскрытия скобок в выражении выше, при x_i = 2^n_i - 1. Но вот только в формуле раскрытия этого выражения участвуют как суммы с четным количеством множителей, так и с нечетным. А у нас только с четным. Как нам тогда это исправить? Что нужно сделать, чтобы у нас каким-то образом убрались, уничтожились нечетные слагаемые?

Подсказка 5

Нужно подставить в выражение уже -(2^n_i - 1). Тогда, сумма в подстановках с минусом и без, не будет содержать слагаемых с нечетным количеством множителей, так как они взаимоуничтожатся. Тогда, это значит, что нам осталось найти значения выражения в подстановке с минусом и с плюсом, и сложить их, после чего поделить на два, ведь все слагаемые с четным числом множителей будут дважды включаться в сумму. Производя эти действия, получим требуемое.

Показать доказательство

Искомое число наборов посчитаем, суммируя количество наборов с заданным числом $k$ ненулевых групп:

При $k= 0$ такой набор единственный;
При $k= 2$ их $∑ ni nj 1≤i<j≤10(2 − 1)⋅(2 − 1);$
При $k= 4$ уже $∑ ni nj nl ns 1≤i<j<l<s≤10(2 − 1)⋅(2 − 1)⋅(2 − 1)⋅(2 − 1);$
$...$
При $k= 10$ в итоге $(2n1 − 1)⋅(2n2 − 1)⋅...⋅(2n10 − 1).$

Определим многочлены

σ (x ,...,x )= 1 0 1 10

σk(x1,...,x10)= ∑ xi⋅...⋅xi ,1 ≤k ≤10 1≤i1<⋅⋅⋅<ik≤10 1 k

Как известно из правила раскрытия скобок, такая сумма всевозможных многочленов это сумма по всем наборам и она равна

∑ 0≤k≤10σk(x1,...,x10)= (x1+1)⋅...⋅(x10+ 1),

Если мы сложим эту сумму с суммой таких же многочленов от отрицательных аргументов, то многочлены с нечётными индексами взаимноуничтожатся:

∑ σk(x1,...,x10)+ ∑ σk (−x1,...,−x10) = 0≤k≤10 0≤k≤10

∑ = 2 . σk (x1,...,x10) 0≤k≤10,k..2

Используем полученные результаты:

∑ n n 2N = 2 ..σk (2 1 − 1,...,2 10 − 1)= 0≤k≤10,k .2

n1 n10 n1 n10 =(2 − 1 +1)⋅...⋅(2 − 1+1)+ (− (2 − 1)+1)⋅...⋅((−2 − 1)+ 1)

2N =2n1+...+n10 + (−2n1 + 2)⋅...⋅(−2n10 + 2)

что и требовалось:

N =2n−1+ 1⋅(2n1 − 2)⋅...⋅(2n10 − 2) 2

Ошибка.
Попробуйте повторить позже

Задача 6#72038

Решите уравнение

5 8cos x− 5cosx − 2cos3x= 1

Источники: Межвед-2022, 11.4 (см. www.academy.fsb.ru)

Подсказки к задаче

Подсказка 1

С косинусом 3x работать неудобно, сразу его раскроем. Теперь хочется уравнение преобразовать так, чтобы справа либо остался 0, либо так и осталась единица, но слева было произведение, которое мы можем оценить.

Подсказка 2

Вынесением общего множителя и использованием тригонометрических формул приходим к равенству cos(x)cos(4x)=1. Попробуем оценить левую часть.

Подсказка 3

Каждый из множителей лежит в определенном промежутке, значит можно разбить решение на два случая.

Подсказка 4

Понятно, что модуль обоих множителей должен быть равен единице. Осталось лишь работать два случая несложных систем)

Показать ответ и решение

5 8cos x− 5cosx − 2cos3x= 1

Используем формулу косинуса тройного угла $cos3x= 4cos3x− 3cosx$ получаем

8cos5x− 5cosx− 2(4cos3x− 3cosx)= 1

8cos5x − 8cos3x+ cosx= 1

Разложим нашу левую часть в произведение чисел, каждое из которых по модулю не больше 1.

cosx(8cos4x − 8cos2x+1)= 1

cosx(−8 cos2x(− cos2x+ 1)+1)= 1

По основному тригонометрическому тождеству получаем

cosx(−8cos2x sin2x+ 1)= 1

По формуле синуса двойного угла получаем

cosx(−2sin22x+ 1)=1

По формуле косинуса двойного угла получаем

cosxcos4x= 1

Так как $− 1≤ cosx ≤1$ и $− 1 ≤cos4x ≤1,$ то равенство возможно только в двух случаях

{ cosx= 1 { cosx= −1 cos4x= 1 или cos4x= −1

Рассмотрим систему

{ cosx= 1 cos4x= 1

Решим уравнение $cosx= 1.$ Получаем $x= 2πn, n∈ ℤ.$ Заметим, что эти решения также являются и решениями второго уравнения системы, поэтому для первой системы имеем $x =2πn, n ∈ℤ.$

Рассмотрим теперь вторую систему

{ cosx =− 1 cos4x= −1

Решим уравнение $cosx= −1.$ Получаем $x= π +2πn.$ Подставим эти решения во второе уравнение системы и получим $cos4(π +2πn)= cos(4π+8πn)= 1$ — противоречие. Значит, у второй системы нет решений.

Ответ:

$2πn,n∈ ℤ$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#72039

Обозначим через $a n,m$ число, полученное записью подряд всех натуральных чисел от $n$ до $m,$ здесь $n$ и $m$ — натуральные числа, причем $n >m ≥ 1.$ Так, например, число $a4,2 =432,$ а число $a11,7 =1110987.$ Докажите, что среди таких чисел есть число, делящееся на $2022.$

Источники: Межвед-2022, 11.7 (см. www.academy.fsb.ru)

Подсказки к задаче

Подсказка 1

Наверное, конкретные m и n мы не предъявим, а нужно как-то построить их. Тогда полезно поискать какие-то свойства таких чисел. Подумайте, что мы можем сказать про разность a(m,1)-a(n,1)...

Подсказка 2

Из определения этих чисел следует, что это будет a(m,n+1)*10ⁿ. Тогда, если a(m,1)-a(n,1) поделится на 1011, то и a(m,n+1)*10ⁿ поделится на 1011. Найдутся ли такие m и n?

Подсказка 3

Найдутся! Действительно, если чисел a(k,1) бесконечно много, то существуют два числа a(m,1) и a(n,1) такие, что их остатки при делении на 1011 совпадают. Это значит, что a(m,n+1)*10ⁿ делится на 1011⇒a(m,n+1) делится на 1011. Осталось только придумать что-то с четностью. Когда число a(m,n+1)- четное?

Подсказка 4

Когда n- нечетное! Подумайте, сможем ли мы найти такую пару a(m,1) и a(n,1), где m и n- оба нечетные, и завершите решение!

Показать доказательство

Рассмотрим числа вида $a n,1$ , где $n$ — нечётное. Так как чисел указанного вида бесконечно много, то среди них найдутся два числа $a n,1$ и $ak,1,n> k,$ имеющие одинаковые остатки от деления на $2022.$ Тогда разность $an,1− ak,1$ делится нацело на $2022.$ При этом $n−k an,1 − ak,1 =an,k+1⋅10$ и число $an,k+1$ является чётным. Так как $2022 =2 ⋅1011$ и числа $1011$ и $n−k 10$ взаимно просты, то число $an,k+1$ делится нацело на $1011,$ а следовательно, и на $2022.$

Ошибка.
Попробуйте повторить позже

Задача 8#72040

Решите уравнение

2 2 x + y +1= 6xy,

где $x$ и $y$ — натуральные числа.

Источники: Межвед-2022, 11.8 (см. www.academy.fsb.ru)

Подсказки к задаче

Подсказка 1

У нас есть уравнение второй степени относительно x и y в натуральных числах. В таких случаях бывает полезно рассмотреть его как квадратное относительно одной из переменной. Что мы можем сказать про это уравнение относительно x?

Подсказка 2

Если y- натуральное число, то все коэффициенты этого уравнения целые числа. Тогда, чтобы x был целым, необходимо, чтобы четверть дискриминанта была полным квадратом. Может ли такое быть?

Подсказка 3

D/4=8y²-1. Тогда должно существовать целое t такое, что t²=8y²-1. Какие тогда ограничения, связанные с остатками, накладывается на t?

Подсказка 4

t² должен давать остаток -1 при делении на 8. Но может ли такое быть? Переберите квадраты всех остатков при делении на 8 и убедитесь, что это невозможно!

Показать ответ и решение

Пусть пара натуральных чисел $(x ,y ) 0 0$ удовлетворяет исходному уравнению

2 2 x + y +1 =6xy

(1)

Тогда

1.

Положив $x0 = y0 =a$ и подставив в $(1),$ получим

2a2+ 1= 6a2

Очевидно, что $a ∕∈ ℕ$ . Поэтому $x0 ⁄= y0$ . Без ограничения общности можно считать, что в этой паре $x0 >y0$ . Будем это записывать как $max(x,y )=x . 0 0 0$

2.

По условию, число $x0$ является корнем многочлена

f(x)=x2− 6y0x +y2+ 1 0

(2)

По теореме Виета, этот многочлен еще имеет корень $x2,$ причем

{ x2+ x0 = 6y0 x2x0 = y20 +1

Отсюда следует, что $x2 = 6y0− x0$ и $x2 ∈ ℕ.$ Поэтому уравнение $(1)$ имеет еще одно решение в натуральных числах $(6y0− x0,y0)$

Это означает, что для многочлена $(2)$ справедливы равенства

f(x0)= f(6x0 − y0)= 0

Заметим, что

f(y0)= y20 − 6y20 + y20 + 1< 0

Поэтому число $y0$ лежит между корнями многочлена $(2),$ а именно:

x0 >y0 >6y0− x0

Следовательно,

max(6y0− x0,y0)= y0 < max(x0,y0)

Итак, для любого решения $(x0,y0)$ существует другое решение, у которого максимальный элемент окажется меньше. Таким образом, мы можем строить новые решения, у которых максимальный элемент становится все меньше. Но при этом этот максимальный элемент, постоянно уменьшаясь, остается натуральным числом, что невозможно. Пришли к противоречию. Значит, исходное уравнение $(1)$ решений в натуральных числах не имеет.

Ответ: решений нет