ШВБ 2021
Ошибка.
Попробуйте повторить позже
Функция при всех действительных
удовлетворяет соотношению
Решите уравнение
Источники:
Подсказка 1
У нас всего одно уравнение на две неизвестные f(x) и f((x+1)/(x-1)). Значит, нужно получить ещё одно уравнение, подставив вместо x такое значение, что аргументы функций останутся прежними.
Подсказка 2
Если мы подставим (x+1)/(x-1) вместо x, то мы получим новое уравнение на наши неизвестные. То есть у нас уже имеется система из двух уравнений с двумя неизвестными. Решив её, мы получим f(x).
Сделаем замену:
Тогда функция при всех вещественных
удовлетворяет соотношению
При всех фиксированных значения
и
удовлетворяют системе уравнений:
Подставим первое уравнение во второе:
Решим заданное уравнение:
Ошибка.
Попробуйте повторить позже
При каких целых значениях параметра для корней
уравнения
выражение будет натуральным числом?
Источники:
Из формул для корней уравнения имеем, что
Поэтому выражение из условия равно
Так как — целое, то результат будет натуральным, когда
Так что возможные значения параметра находятся из
совокупности:
Подходят значения параметра
Ошибка.
Попробуйте повторить позже
При каких значениях параметра площадь фигуры, ограниченной на координатной плоскости
линиями
равна
Источники:
Подсказка 1
Подумайте, что из себя представляют линии x = a - 1 - a² и x = a² - 3a + 1
Подсказка 2
Да, это действительно будут просто вертикальные прямые. Теперь попробуйте визуализировать: что будет представлять собой фигура, ограниченная заданными прямыми?
Подсказка 3
Попробуйте вспомнить, какие есть формулы площади параллелограмма. Какая из них может помочь нам решить задачу, учитывая, что длина одной из сторон — постоянная величина?
Подсказка 4
Учитывая, что у нас фиксированная площадь и одна из сторон так же фиксирована, значит существует и единственное возможное значение длины высоты, опущенной к этой стороне. Попробуйте представить высоту как выражение, зависящее от параметра a.
Рассмотрим и нарисуем графики функций и
![]()
Так как мы работаем в плоскости то
и
являются вертикальными линиями, двигающимися вдоль
при изменении
Получается, что мы должны рассматривать площадь параллелограмма.
Так как и
не зависят от параметра
, то мы можем воспользоваться формулой
где
— длина прямой,
ограниченной нашими функциями, а
— расстояние между вертикальными линиями.
![]()
Заметим, что мы можем очень легко найти:
По условию:
Так же можно представить как:
Осталось лишь найти корни уравнения, когда
Ошибка.
Попробуйте повторить позже
Найдите наибольшее натуральное число для которого верно неравенство
Источники:
Подсказка 1
Из условия становится понятно, что нам пригодится формула суммы кубов;) Если Вы её забыли — не беда, можно выразить её по индукции или через сумму четвёртых степеней. Но для этого нам понадобится, например, формула суммы последовательных квадратов.
Подсказка 2
После того, как мы выразим обе суммы в виде дробей, можно будет заметить, что у них есть общий множитель, а справа стоит 0. Это нам намекает на то, что нужно попытаться разложить левое выражение на множители! Осталось лишь разобрать знаки скобочек и записать новое неравенство на x ;)
Вычислим сумму
Заметим, что сумма кубов до вся сокращается, и остаётся только
Отсюда выразим сумму квадратов.
Теперь проделаем аналогичные преобразования для вычисления суммы
Все эти формулы, конечно, желательно и так помнить, но если забыли, то можно будет вывести так или по индукции. Тогда возвращаясь к неравенству
Отсюда получаем, что наибольшее натуральное значение, при котором верно равенство, равно
Ошибка.
Попробуйте повторить позже
На стороне треугольника
отмечена точка
так, что
Около треугольника
описана
окружность. Через точку
и точку
лежащую на стороне
проведена прямая, которая пересекает окружность в точке
причем
Найдите
если
— биссектриса треугольника
Источники:
Подсказка 1
На картинке у нас есть окружность, а также равные из условия углы. Давайте тогда попробуем записать цепочки равных и вывести из этого что-то полезное.
Подсказка 2
Здорово, оказывется, у нас проведена касательная к окружности, а треугольники AKC и BAC подобны! Воспользуемся этим и условием, чтобы посчитать некоторые отрезки ;) Сейчас наша цель — делать картинку как можно яснее.
Подсказка 3
Таким образом, из подобий и того, что у нас проведена биссектриса, можно посчитать практически все отрезки треугольника ABC. Но как добраться до отрезка, который является частью хорды в окружности? Давайте введём переменные и воспользуемся тем, что знаем об отрезках хорды!
Подсказка 4
AD * DB = PD * DN. А произведение секущей на её внешнюю часть равно квадрату касательной! Отсюда можно найти ответ ;)
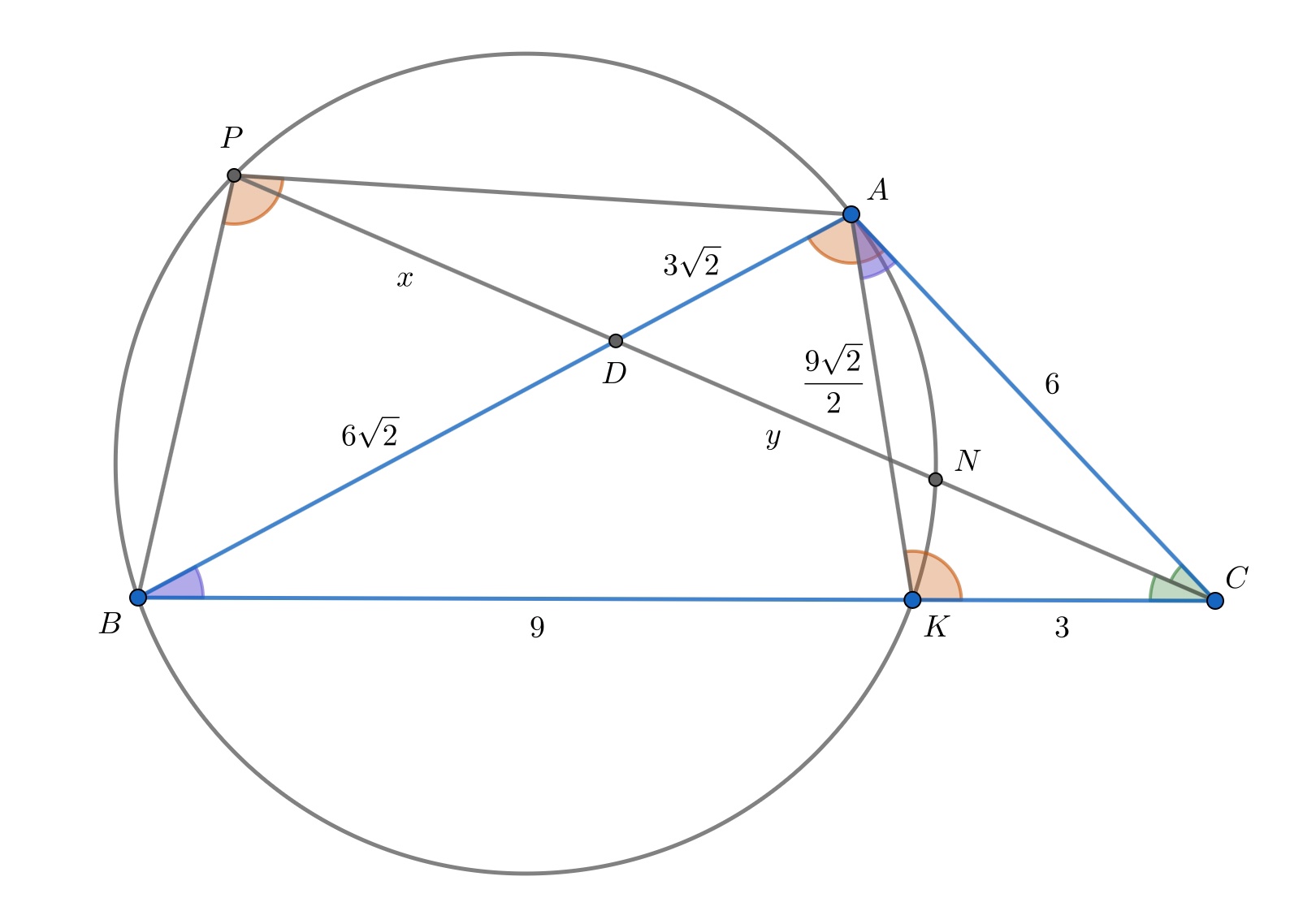
Из условия мы знаем, что
а из вписанного четырёхугольника
Откуда получаем, следующие
равенства
Значит, отрезок является отрезком касательной к окружности. Теперь мы понимаем, что
подобен
Запишем
соответствующие отношения сторон и подставим значения из условия:
Так как мы знаем, что
— биссектриса, то запишем свойство, подставив известные значения
К тому же мы нашли поэтому
Давайте теперь запишем формулу для биссектрисы и вычислим
её:
Пусть
где
точка пересечения прямой
с окружностью,
Четырехугольник
вписан в
окружность, откуда из произведения отрезков хорд
По свойствам касательных и секущих к окружности имеем
Теперь осталось только решить систему из полученных уравнений в
пункте
Откуда Решив уравнение, получим
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при которых система
имеет решения. Укажите эти решения при найденных значениях параметра
Источники:
Подсказка 1
С тригонометрическими функциями работать неприятно, а в рамках таких нетривиальных равенств даже больно. Давайте замену x = 5cos t, y = 5sin t. Чтобы замена была равносильной, добавим в систему третьей уравнение x²+y²=25.
Подсказка 2
Давайте обратим внимание на второе равенство. Предлагается рассмотреть три случая: x < 0, 0 < x < 4, 4 < x. В каждом из этих случаев второе уравнение превращается в нечто простое.
Подсказка 3
В каждой в третье уравнение можно вместо y подставить его выражение через a и изобразить область первого неравенства и третьего равенства в осях xa. Дальше останется аккуратно понять, при каких a будут решения.
Сделаем следующие замены:
Имеем
Система распадается на совокупность трёх систем:
В системе координат изобразим решение системы
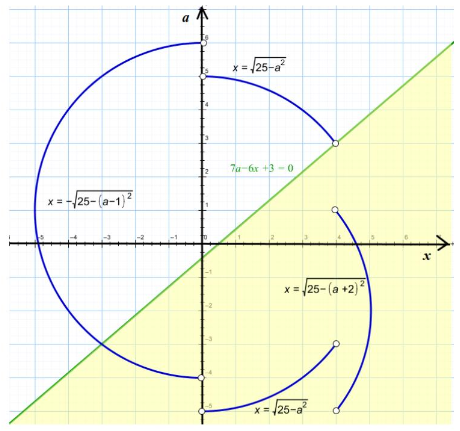
Имеем решение
Тогда
Откуда получается, что
При записи же ответа через нужно учитывать знаки
, т.е.
при
а при имеем
Имеем решение
при
. Тогда
Откуда получается, что
или
3) Имеем решение при
. Тогда
Откуда получается, что
или
при
имеем
при
имеем
при
имеем
при
имеем
Ошибка.
Попробуйте повторить позже
Основанием пирамиды служит прямоугольный треугольник
с катетами
и
Высотой пирамиды
является отрезок
где точка
симметрична точке
относительно середины отрезка
Точка
принадлежит боковому ребру
причем
Найдите площадь сечения пирамиды плоскостью, проходящей через
параллельно гипотенузе основания
и отрезку
если расстояние от точки
до секущей плоскости равно
Источники:
Подсказка 1
Если вы верно построили сечение, то оно должно быть треугольником. Обозначим его через KNL (K на AS, N на BS, L на CS). Пусть A₁ симметрична B относительно A, аналогично определим C₁. Заметим, что треугольники KNL и A₁NC₁ подобны.
Подсказка 2
Отметьте на BD такую точку R, что NR || SD. Тогда NR перпендикулярна плоскости основания. Также проведите через R Прямую, перпендикулярную A₁C₁ и пересекающую её в Q. Что можно сказать про NQ в треугольнике A₁NC₁?
Подсказка 3
Также давайте проведём через B прямую параллельно A₁C₁ и пересечём её с RQ в B₁. Расстояние от B до секущей плоскости равно расстоянию от B₁ до секущей плоскости (почему?). Дальше осталось аккуратно посчитать ответ.
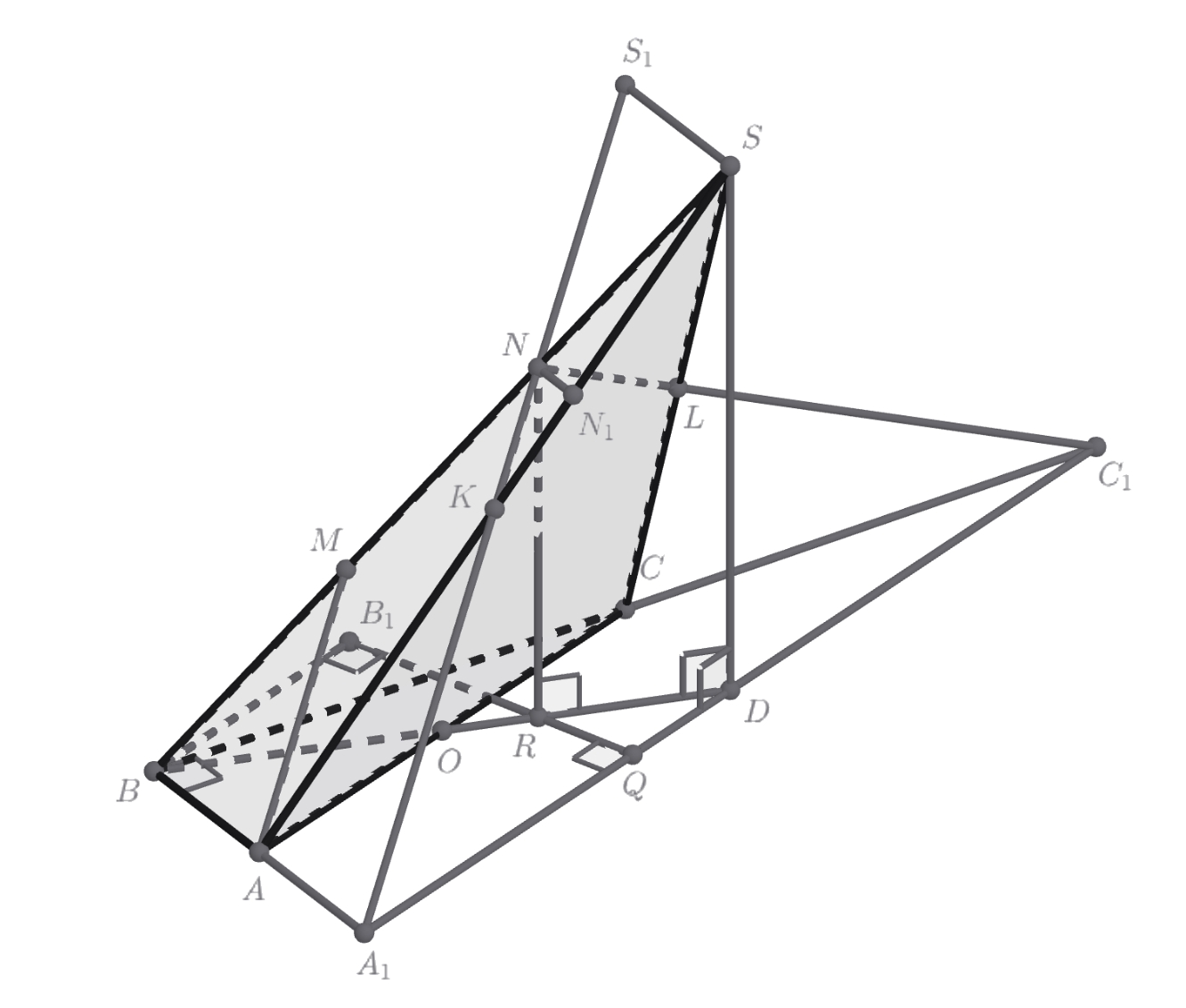
Треугольник — прямоугольный,
точка
точка
симметрична
относительно
Секущая плоскость
проведена через точку
расстояние
от точки
до плоскости
Проведём через точку
прямую
параллельную
такую, что
Также отметим точку
на
такую, что
средняя линия
и
пересекает
в точке
Тогда
видим, продлив
до пересечения в точке
с прямой, проходящей через
паралелльно
и лежащей в плоскости
что
К тому же
Проведём через точку в плоскости
прямую, параллельную
и пересекающую
в точке
Тогда получаем,
что
Аналогично, проведя подобные рассуждения в плоскости получаем, что
где
точка пересечения
и
Плоскость
содержит
сечение — треугольник
Для площадей, в силу подобия треугольников, имеем соотношение
Отметим на
точку
такую, что
Тогда
Через
проведём прямую
и пусть она пересекает прямую, параллельную
и проходящую через
в точке
Тогда по теореме о
перпендикулярах
откуда
Найдем
Поскольку
и расстояние
от точки
до плоскости
равно расстоянию от точки
до
плоскости
Длина отрезка
равна высоте треугольника
Имеем Пусть
. Тогда
Ошибка.
Попробуйте повторить позже
Искусственный спутник (ИСЗ) движется по круговой орбите вокруг Земли (имеет форму шара) на высоте равной радиусу Земли
км, с периодом обращения
ч и постоянной угловой скоростью
Для того, чтобы можно было наблюдать за
спутником с поверхности Земли, он должен находиться выше плоскости горизонта. Определите:
а) продолжительность наблюдения спутником (в минутах) от момента его появления над горизонтом до момента захода за горизонт, если траектория ИСЗ проходит ровно над головой наблюдателя;
б) плоский угол при вершине конуса обзора поверхности Земли с ИСЗ (в градусах).
Источники:
Подсказка 1
С первого взгляда что-то очень непонятное, но давайте постараемся это нарисовать. Нарисуем две концентрические окружности (Земля и орбита) и линию горизонта.
Подсказка 2
Вспомним из физики, как мы можем выразить время полёта. Ага! Время полёта можно представить как длину дуги, поделённую на угловую скорость из условия.
Подсказка 3
Длину дуги можно найти, зная величину центрального угла. А как же найти величину центрального угла? Проведём радиус и касательную и внимательно посмотрим на получившийся треугольник. Ведь мы можем найти его углы!
Пусть наблюдатель находится в точке
— линия пересечения плоскости горизонта и плоскости орбиты. Спутник проходит над
головой наблюдателя.
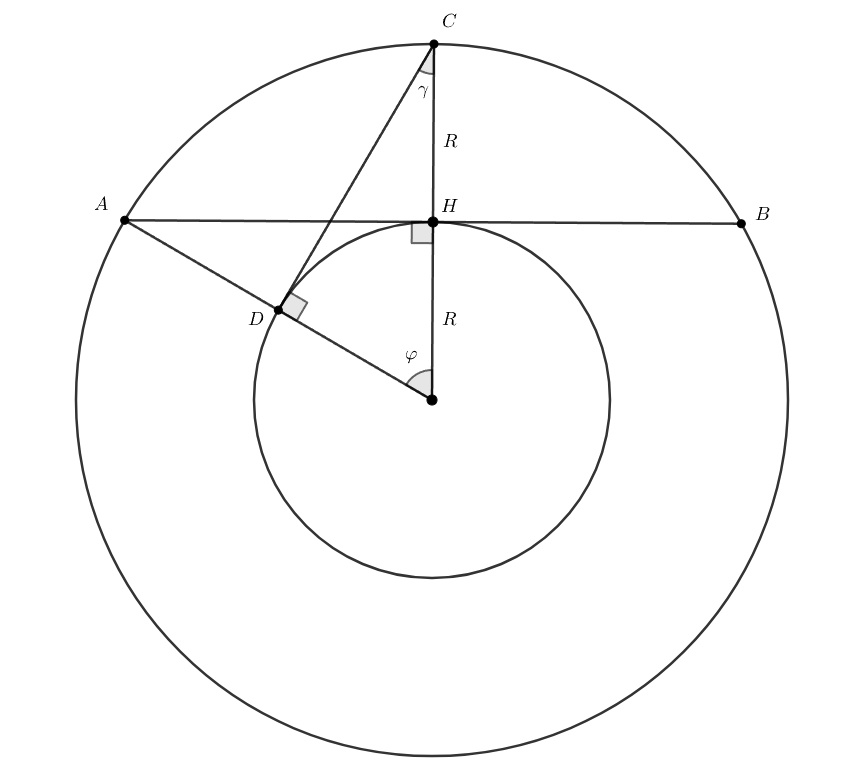
При движении спутника из точки в точку С по дуге окружности, его проекция на Землю двигается из точки
в
точку
Угловая мера этой дуги
равна величине центрального угла. Учитывая симметрию, получим время
наблюдения
Угол находим из прямоугольного треугольника
следовательно, мин.
Угол обзора участка Земли с орбиты равен углу или
градусов.
а) минут, б)
градусов
Ошибка.
Попробуйте повторить позже
На боковых рёбрах правильной треугольной пирамиды
соответственно выбраны точки
так, что
. Точка
— центр сферы, описанной около пирамиды
Докажите, что прямая
перпендикулярна
плоскости
Найдите радиус этой сферы и объём пирамиды
если сторона основания
боковое ребро
Подсказка 1
Посмотрим на цепочку соотношений из условия, которая равна 3. Почему именно эти отношения влияют на расположение точек A₁, B₁, C₁ на рёбрах пирамиды? Возможно, стоит посмотреть на подобия каких-то треугольников.
Подсказка 2
Иногда можно использовать идею проецирования центра сферы на разные плоскости. Подумайте, почему такая проекция на боковые грани позволяет утверждать, что есть общий перпендикуляр к двум прямым, пересекающимся на плоскости из условия.
Подсказка 3
Воспользуемся теоремой о трёх перпендикулярах. К какой прямой и плоскости её стоит применить?
Подсказка 4
Применяем теорему о трёх перпендикулярах к TO и пересекающимся B₁C и A₁C в плоскости A₁B₁C и доказываем требуемое. Теперь перейдём ко второй части задачи. Для этого полезно рассмотреть высоту пирамиды и вспомнить, что в основании неё лежит равнобедренный треугольник. Подумайте, какие дополнительные точки (например, на рёбрах пирамиды) могут упростить вычисления.
Подсказка 5
Для нахождения объёма пирамиды может оказаться нужным найти её высоту, введя дополнительный угол и его синус/косинус, установить, каким отношением связаны основания A₁B₁ и AB и использовать тот факт, что T лежит на TO, которая по доказанному перпендикулярна плоскости из условия. Для нахождения радиуса вспоминаем формулу со стороной и синусом противолежащего угла!
1) Докажем, что прямая перпендикулярна плоскости
Точка
лежит в плоскости
,
— середина
Спроецируем
точку
на плоскость
ее проекция
центр описанной около треугольника
окружности. Прямая
— проекция
на плоскость
Докажем, что
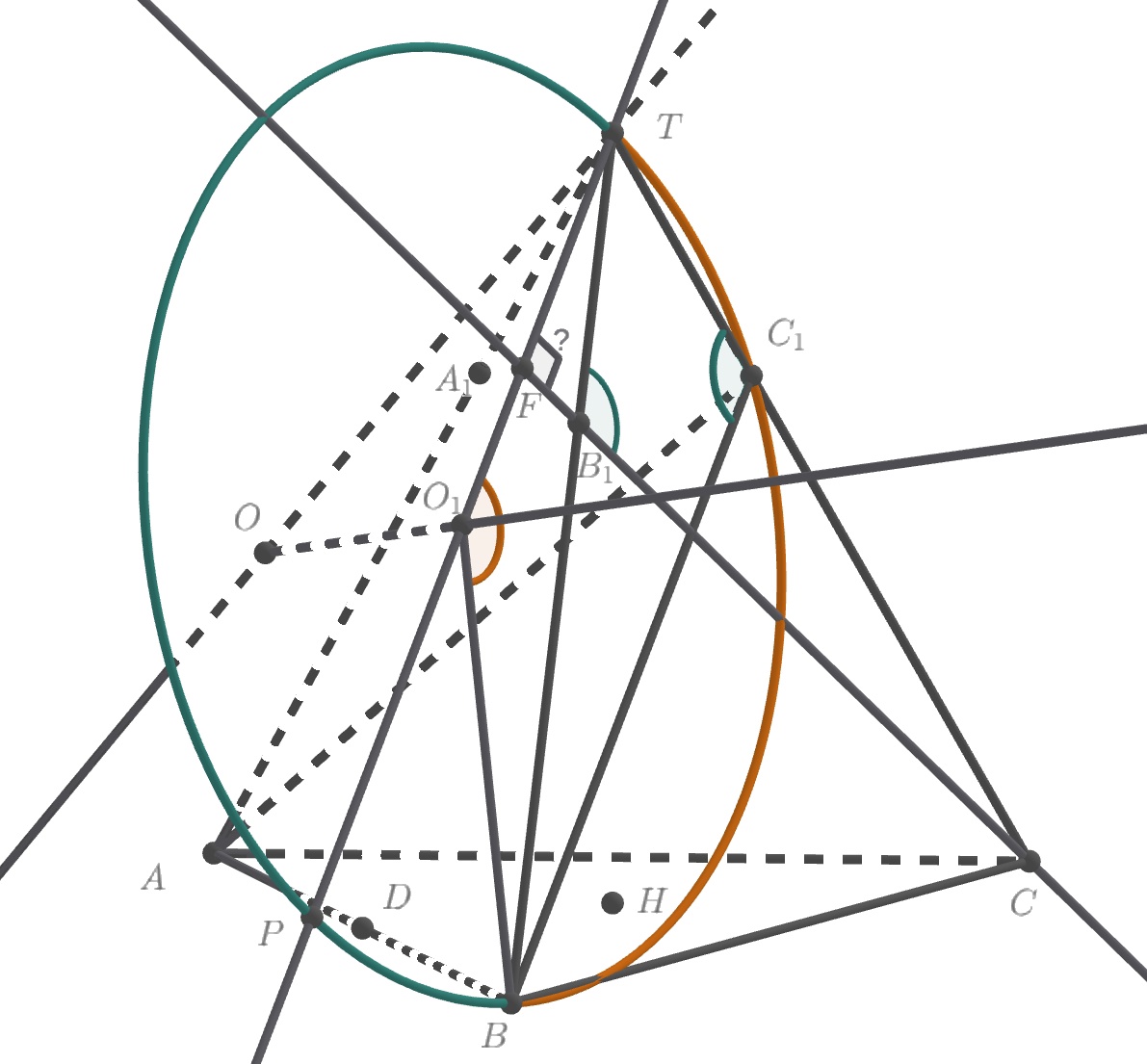
Поскольку то
подобен
тогда
Докажем, что
т.е.
— точка пересечения прямых
и
По свойству вписанных углов
имеем:
Пусть — диаметр рассматриваемой окружности. Тогда
Таким образом,
Аналогично доказывается, что проекция на плоскость
перпендикулярна
Согласно теореме о трех перпендикулярах,
также будет перпендикулярна двум пересекающимся прямым
и
лежащим в плоскости
следовательно,
2) Обозначим через длину стороны основания пирамиды
Обозначим через
длину бокового ребра пирамиды
Пусть
— высота пирамиды
Тогда
В основании пирамиды
лежит
равнобедренный треугольник
— его высота,
— середина
Высота
пирамиды
проведенная из вершины
лежит на прямой
Для вычисления объема пирамиды
нужно найти
и
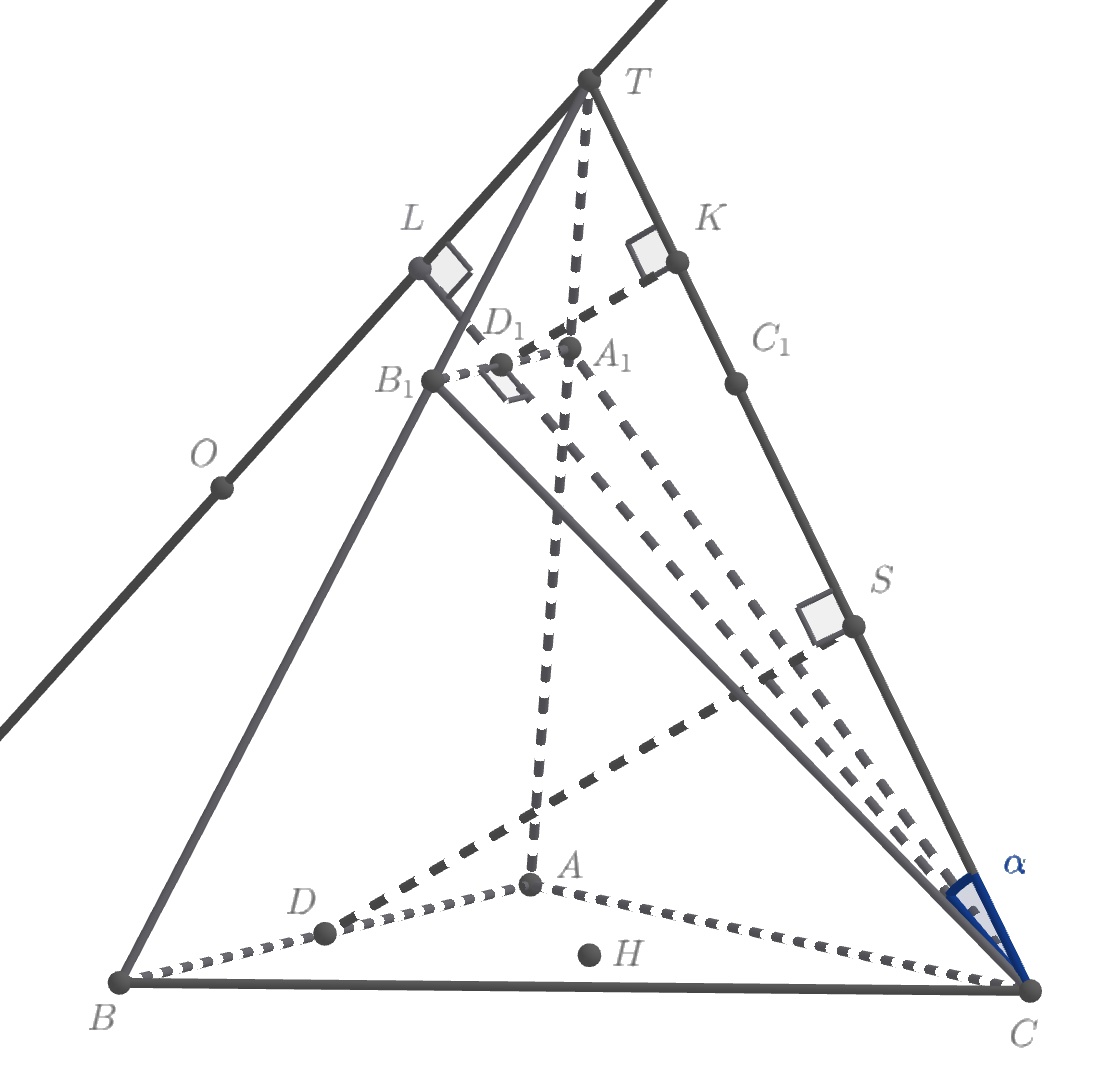
На боковом ребре отметим точки
и
так, что
Пусть Тогда
Значит,
Итак, объем пирамиды вычисляется по формуле


