ШВБ 2022
Ошибка.
Попробуйте повторить позже
Найдите все варианты троек , при которых выполняется уравнение
Источники:
Подсказка 1
С первого взгляда очень страшное выражение: множество корней и модулей, — не совсем понятно, что с ними делать. Но как только видим справа ноль, сразу становится легче. Какое самое важное ограничение есть у корней, которое необходимо вспомнить?
Подсказка 2
Верно, все они неотрицательные! То есть задумаемся. Если хотя бы один из них не ноль, то тогда всё выражение точно больше нуля, и равенства не будет. Как теперь это можно переписать с точки зрения алгебры?
Подсказка 3
Да, можно записать как систему, что все три корня равны нулю. Теперь внимательно посмотрим на получившиеся уравнения. Первое из них содержит только одну переменную. Значит, его легко решим. В остальных уравнениях видим похожую идею, как в изначальном уравнении. Когда у нас произведение чисел равно нулю? Как можно это переписать?
Подсказка 4
Верно, это уже будет совокупность, что какое-то из них равно нулю. Далее применяя эти две идеи, можем решить и третье уравнение исходной системы. Осталось только верно записать решение и победа!
Так как каждое слагаемое неотрицательное, уравнение равносильно следующей системе
Если то
— любое, а
Если то
Итого получаем тройки
Ошибка.
Попробуйте повторить позже
В лаборатории имеются колбы двух размеров (объемом и объемом
) в суммарном количестве 100 штук, причем колб каждого
размера не менее трех. Лаборант поочередно случайно выбирает три колбы, и первую из них полностью заполняет 80-процентным раствором
соли, вторую полностью заполняет 50-процентным раствором соли, а третью колбу полностью заполняет 20 процентным раствором соли.
Затем он сливает содержимое этих трех колб в одну чашу и определяет процентное содержание соли в ней. При каком наименьшем
количестве больших колб
событие «процентное содержание соли в чаше находится в пределах от
до
включительно» будет
случаться реже события «при случайном бросании двух симметричных монет выпадает орел и решка (в любом порядке)»? Ответ
обосновать.
Источники:
Подсказка 1
Для начала, надо обозначить количество больших и малых колб, учитывая, что их сумма равна 100 и количество каждого типа не меньше 3. Теперь, давайте переберем все случаи, которые могут быть при вытаскивании трёх колб и поймем, какие нам подходят, а какие нет.
Подсказка 2
Да, если мы вытащим три большие колбы, то содержание соли будет 50 процентов, это нам подходит, так как(0.8V+0.5V+0.2V)/(3V) = 0.5. Переберите остальные случаи, а после этого вспомните, что мы как-то обозначили количество больших и малых колб(например, N - количество больших колб, а n - маленьких)
Подсказка 3
Верно, если мы переберем все случаи, то получим, что условие на процентное содержание выполняется, когда у нас 3 больших или три малых колбы, также если в маленькую колбу залить 50% раствор, а остальные колбы большие и последний случай, когда в большую колбу залили 50% раствор, а остальные колбы маленькие! Осталось написать уравнение через определение вероятности, ведь всего вариантов выбрать три колбы(если их пронумеровать, чтобы все они были различны) 100*99*98
Подсказка 4
После приведения подобных у нас останется уравнение ((N-50)²+2450)/4950 < 1/2. Остаётся найти такое минимальное N(мы сравниваем именно с одной второй, так как вероятность выпадения одного орла и одной решки за 2 броска равна 1/2)
Если — имеющееся количество больших колб в лаборатории,
то
— имеющееся количество малых колб в
лаборатории,
Для события
содержание соли в чаше находится в пределах от
до
включительно
необходимо найти такое наименьшее
что вероятность
Мысленно перенумеруем все имеющиеся в лаборатории колбы — присвоим им личные номера от 1 до 100. И тогда равновероятными
исходами этого эксперимента будут упорядоченные тройки различных личных номеров последовательно выбираемых лаборантом колб:
Общее количество таких исходов равно
Вычислим теперь количество благоприятных исходов для появления события Рассмотрим следующие случаи, определяемые
размерными типами выбранных колб.
- 1.
-
Лаборант выбирает три большие колбы — тип [Б, Б, Б]. Тогда процентное содержание соли в чаше в результате описанных манипуляций лаборанта окажется равным величине:
Такой выбор благоприятствует появлению события
Количество элементарных исходов данного типа, очевидно, равно
- 2.
-
Лаборант выбирает три маленькие колбы — тип [м, м, м]. Процентное содержание соли в чаше:
Такой выбор благоприятствует появлению события
Количество исходов в этом случае равно
- 3.
-
Лаборант выбирает сначала две большие колбы, затем маленькую — тип [Б, Б, м]. Процентное содержание соли в чаше:
Такой выбор не благоприятствует появлению события
- 4.
-
Лаборант выбирает последовательно большую, малую и большую колбы — тип [Б, м, Б]. Процентное содержание соли в чаше:
Такой выбор благоприятствует появлению события
Количество элементарных исходов в этом случае равно
- 5.
-
Лаборант выбирает сначала малую колбу, затем две большие колбы — тип [м, Б, Б]. Процентное содержание соли в чаше:
Такой выбор не благоприятствует появлению события
- 6.
-
Лаборант выбирает сначала две малые колбы, затем большую колбу — тип [м, м, Б]. Процентное содержание соли в чаше:
Такой выбор не благоприятствует появлению события
- 7.
-
Лаборант выбирает последовательно малую, большую и малую колбы — тип [м, Б, м]. Процентное содержание соли в чаше:
Такой выбор благоприятствует появлению события
Количество элементарных исходов в этом случае равно
- 8.
-
Лаборант выбирает сначала большую, затем две малые колбы — тип [Б, м, м]. Процентное содержание соли в чаше:
Такой выбор не благоприятствует появлению события
.
Вычисляем вероятность события A (по формуле классической вероятности):
Отсюда имеем
И значит,
Ошибка.
Попробуйте повторить позже
В выпуклом четырехугольнике длины сторон
и
равны,
— биссектриса угла
Найдите
косинус угла
если
— точка пересечения диагоналей
и
и
Источники:
Подсказка 1
Сразу запишем все отрезки через переменные, пользуясь свойством биссектрисы) Как воспользоваться тем, что у четырехугольника есть две равные стороны? Не забываем, что диагональ DB является биссектрисой!
Подсказка 3
Произведение отрезков диагонали равны! Запишем это, и, т.к. у нас все отрезки теперь выражены с помощью двух переменных, сможем применить теорему косинусов, чтобы избавиться от одной переменной) Осталось лишь понять, как искать косинус нужного угла, если мы знаем отношения практически всех отрезков на картинке!
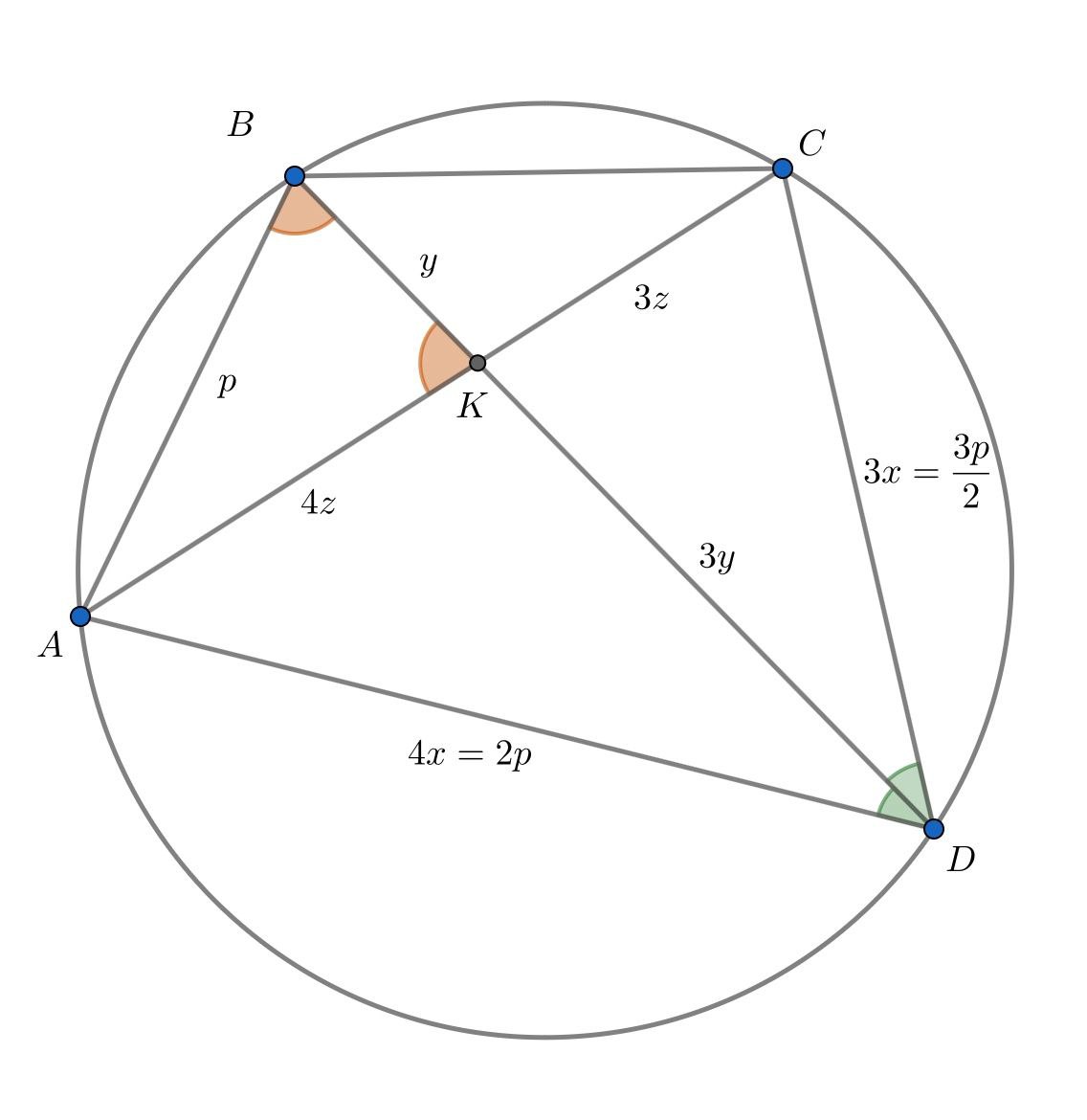
пусть
пусть
— биссектриса треугольника
Точка является точкой пересечения серединного перпендикуляра к диагонали
и биссектрисы угла
в выпуклом
четырехугольнике
Следовательно, около этого четырехугольника можно описать окружность.
Действительно, опишем окружность около треугольника обозначим точку пересечения биссектрисы угла
с окружностью через
Тогда по свойству вписанных углов дуги
и
будут равны, хорды
и
тоже будут равны, треугольник
будет равнобедренным, и серединный перпендикуляр к диагонали
и биссектриса угла
будут пересекаться в точке
Следовательно,
Поскольку около четырехугольника можно описать окружность, то для его диагоналей верно равенство
Треугольник подобен
, и
, пусть
поэтому
По теореме косинусов для треугольников и
с учетом
имеем
Для равнобедренного треугольника имеем
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при которых система
имеет шесть различных решений.
Источники:
Подсказка 1
Система только кажется страшной, а когда так кажется, то скорее всего за ней спрятано что-то простое. Давайте тогда попробуем разбить наши сложные уравнения на несколько простых, а ещё попутно не забудем собирать ограничения на ОДЗ!
Подсказка 2
Во втором уравнении как-то странно выбивается log₂(a²), ведь остальные логарифмы по основанию "a". Может, стоит его перевернуть? Не забывайте, что мы не всегда вправе так делать, вспомните, какими утверждениями мы пользуемся при таком переходе, чтобы он был равносильным.
Подсказка 3
Первое уравнение легко распадается на 2 независимых, а значит, нашу систему можно переписать как совокупность систем и работать с каждой из них по отдельности. Мы могли бы поверить в светлое будущее и понадеяться, что в сумме полученные системы имеют не более 6 решений, чтобы получить ещё побольше информации, но, порисовав графики, можно убедиться, что решений может быть больше. Поэтому придётся искать, сколько решений имеет каждая из систем по отдельности для всех "a".
Подсказка 4
Давайте начнём с системы ay-ax+2=0; |xy|=4a. Про I, II, III четверти мы всё понимаем, а вот с IV стоит поработать. Поэтому мы сразу можем сказать, что работаем при x > 0, y < 0. Интуитивно хочется сказать, что нас волнует только точка (1/a, -1/a) прямой ay-ax+2=0, которая сама бегает по прямой y = -x, а именно под или над веткой гиперболы она лежит. Ещё очень хочется сказать, что ближайший маршрут от точки (0,0) до ветки лежит на прямой y = -x. А если что-то хочется, то надо бы попробовать это доказать. Подумайте, как можно понять, сколько общих точек с веткой гиперболы из IV четверти имеет наша прямая для всех "a"?
Подсказка 5
Мы же можем перейти к расстояниям от интересующих нас точек до точки (0,0), ведь они обе лежат на прямой y=-x и на ней же лежит отрезок из начала координат до ближайших точек соответствующих графиков, а зная расстояние до каждой из них, мы с лёгкостью сможем сказать, сколько решений имеет данная система.
Подсказка 6
Чтобы найти длину достаточно знать координаты каждой из указанных точек и воспользоваться теоремой Пифагора. На самом деле для нахождения кратчайшего расстояния до прямой ay-ax+2=0 можно было воспользоваться фактами для прямоугольного треугольника, который образуется пересечением этой прямой с осями, такой приём может сильно сократить вычисления в более сложных задачах.
Подсказка 7
Наконец перейдём ко второй системе. Теперь у нас один из графиков не прямой, а "уголок" ("галочка", "клин"). Чтобы хорошо себе представить его поведение хорошо бы знать, как меняется его "вершина" и "ветки" при изменении "a".
Подсказка 7
Можно заметить, что коэффициент перед "x" от "a" не зависит, а значит его ветки постоянны, а если вместо "x" подставить "a" (момент смены знака модуля или наклона прямой), то можно заметить, что y = -a, а значит, его вершина лежит на прямой y=-x, и мы снова свели задачку к IV четверти, но у нас уже есть все инструменты для решения аналогичной задачи!
Подсказка 8
Не забудьте про то, что если первая система имеет A решений, вторая - B, то необязательно, что их совокупность будет иметь A+B решений, ведь некоторые могут совпасть...
Упростим второе уравнение системы:
I.
1) Система имеет 2 различных решения, если
Найдем эти решения:
2) Система имеет 3 различных решения, если
Найдем эти решения:
3) Система имеет 4 различных решения, если
Найдем эти решения:
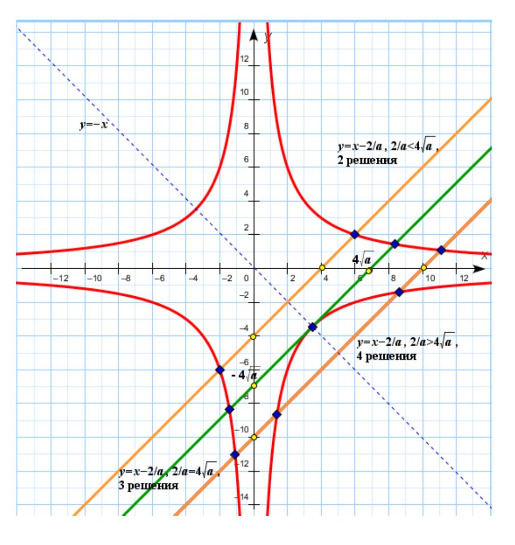
II.
при
имеем
при
имеем
1) Система имеет 2 различных решения, если
Найдем эти решения:
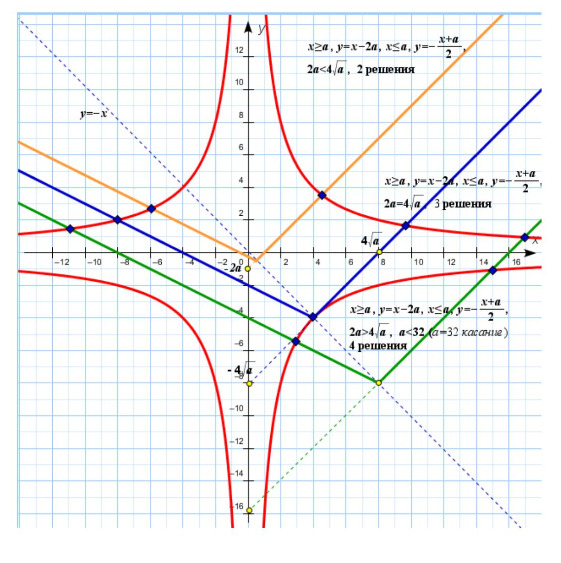
2) Система имеет 3 различных решения, если
Найдем эти решения:
3) Найдем значение параметра при котором прямая
будет касаться графика гиперболы
Тогда при
система будет иметь 4 решения:
Найдем четвертое решение:
4) При система будет иметь 5 различных решений:
5) Система имеет 6 различных решений при :
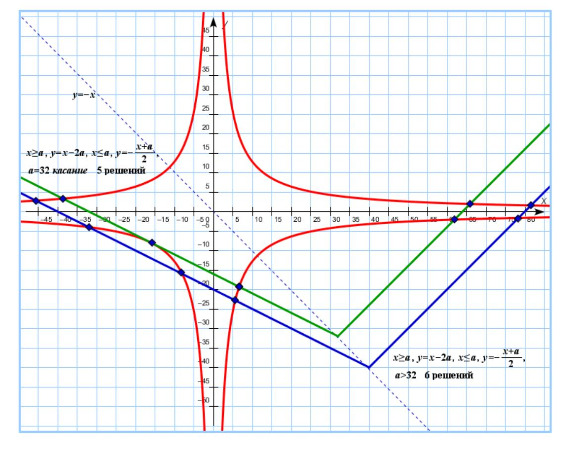
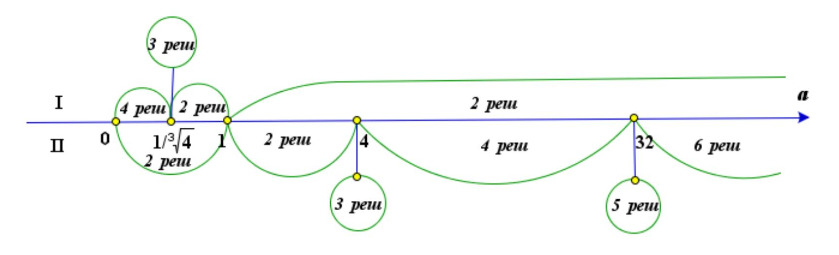
Возможны следующие случаи совпадения решений в I и II случаях:
1) в этом случае нет решений;
2) прямые и гипербола
пересекаются в одной точке, но этот случай возможен при
и в этом случае
будет 7 решений.
Ошибка.
Попробуйте повторить позже
Шар радиуса лежит внутри правильной четырехугольной пирамиды
со стороной основания 8 и высотой 3.
Этот шар касается плоскости основания
пирамиды и боковых граней
и
Плоскость
касается
шара, проходит через точку
середину
ребра
и пересекает ребро
в точке
Найдите объем пирамиды
Источники:
Подсказка 1.
Сразу же введём основание высоты пирамиды (например, через точку H) и центр шара (например, через точку O). Раз в условии у нас правильная пирамида, то центр данного шара лежит в плоскости SHC. Тогда удобно будет провести прямую, проходящую через центр O параллельно SH (пусть это прямая PR). Мы сразу знаем OP, ведь он равен радиусу, а также то, что RP перпендикулярен плоскости основания пирамиды. Введём коэффициент подобия треугольников SCH и RCP (пусть он равен 1/k). Тогда, зная SH, мы можем выразить PR через k. Хорошо бы было выразить ещё отрезки через k, чтобы впоследствии прийти к уравнению и найти k. Попробуйте сделать это в плоскости ABCD.
Подсказка 2.
В плоскости ABCD мы можем провести прямую, проходящую через P параллельно AB. Пусть она пересекает BC в точке N. Тогда, так как ABCD — квадрат, то AH = HC, и с помощью этого мы легко можем выразить PN через AB и k. Теперь можно заметить, что точка касания шара и плоскости SBC лежит на RN. Что тогда мы можем сказать про треугольники ROE и RPN?
Подсказка 3.
Верно, они подобны. Тогда, записав подобие, мы можем получить уравнение на k, откуда k = 1/3. Отлично, теперь пора возвращаться к плоскости из условия. Чтобы найти объём MBCK, нужно найти высоту из M на BCK (пусть это отрезок MG) и площадь треугольника BCK. С треугольником BCK нет никаких проблем, ведь мы знаем сторону квадрата ABCD и отношение CK к KD, а значит, можем найти любой элемент треугольника. Но как же найти MG? Попробуйте выразить его через SH и коэффициент подобия треугольников MCG и SCH (пусть он равен n). Чтобы найти n, можно использовать угол между плоскостями MKB и KBC, опустив высоту GV на BK.
Подсказка 4.
Используя подобие треугольников VFG и FKC (F является точкой пересечения BK и AC), мы можем выразить GV через n. Тогда мы можем выразить тангенс угла MVG через n. Отлично! Теперь осталось лишь найти этот угол. Мы знаем, что он является линейным углом двугранного угла между плоскостями MKB и KBC. Для решения задачи мы ещё не использовали, что плоскость MKB касается шара (пусть точка касания — точка T). Зная это, мы можем опустить перпендикуляр PQ на BK и получить, что TQP также является линейным углом двугранного угла между плоскостями MKB и KBC. Теперь нужно найти угол TQP. Его не очень удобно искать, однако посмотрите на треугольники OTQ и OQP. Попробуйте найти угол, используя их равенство.
Подсказка 5.
Треугольники OTQ и OQP равны, а значит и углы TQO и OQP. Тогда угол TQP в два раза больше угла OQP. А вот угол OQP легко найти, ведь мы можем выразить PQ через подобие треугольников QFP и KFC, а OP мы знаем. Так мы найдём тангенс угла OQP. Затем по формуле тангенса двойного угла найдём тангенс угла TQP и, подставив в уравнение, найдём n. Осталось лишь подставить n в формулу MG и найти объём.
Поскольку пирамида правильная, то центр
указанного шара лежит в плоскости
, где
— высота пирамиды. Пусть
Обозначим Проведем
— точка касания шара плоскости
пусть радиус шара
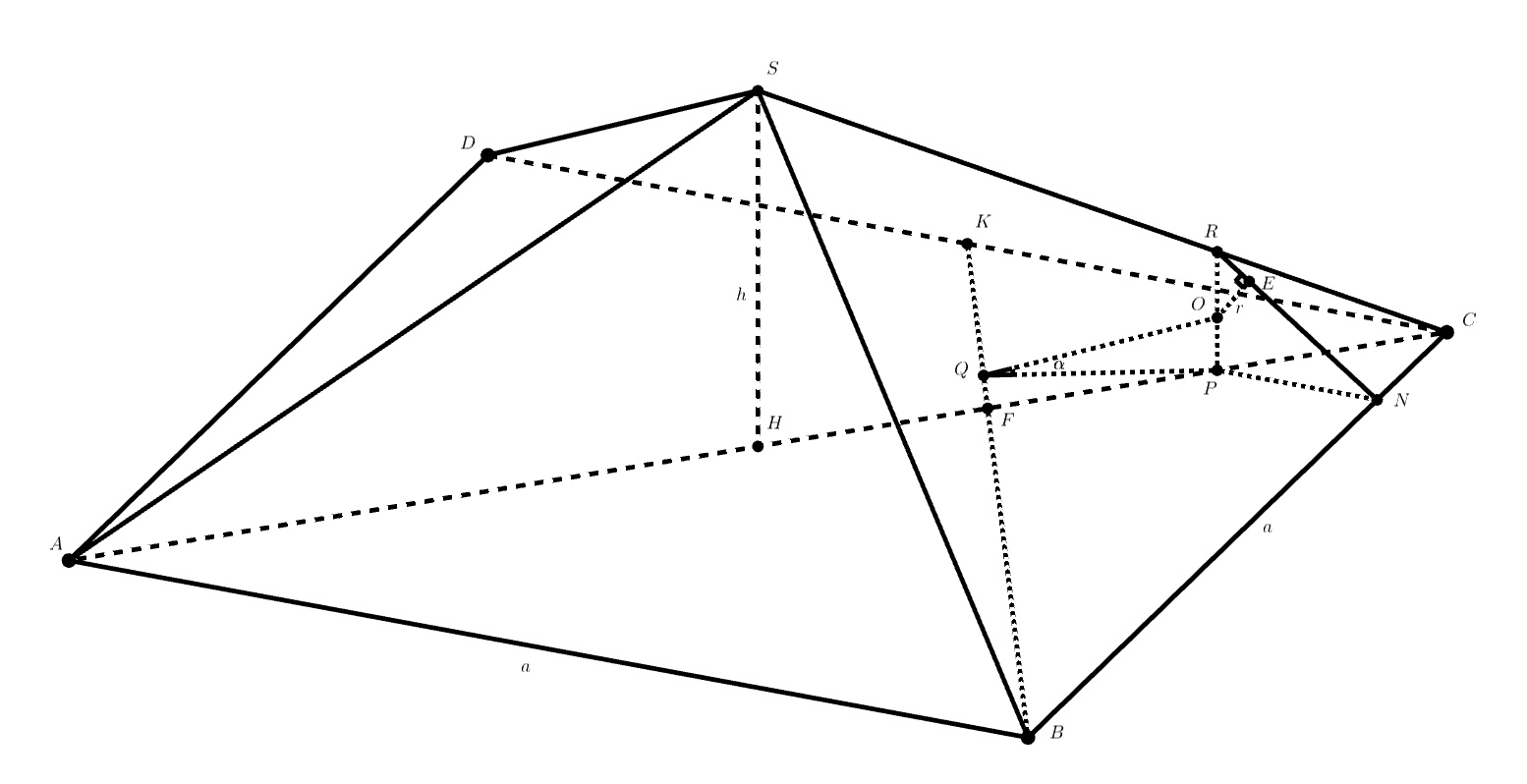
Поскольку то
Треугольники
и
подобны, и
или
По условию задачи Тогда
Точка — точка пересечения
и
тогда
Поскольку
Пусть . Тогда
Если
то
Угол между плоскостью
и плоскостью основания
равен
Тогда
Пусть — отрезок перпендикуляра, опущенного из точки
на плоскость основания
, и
.
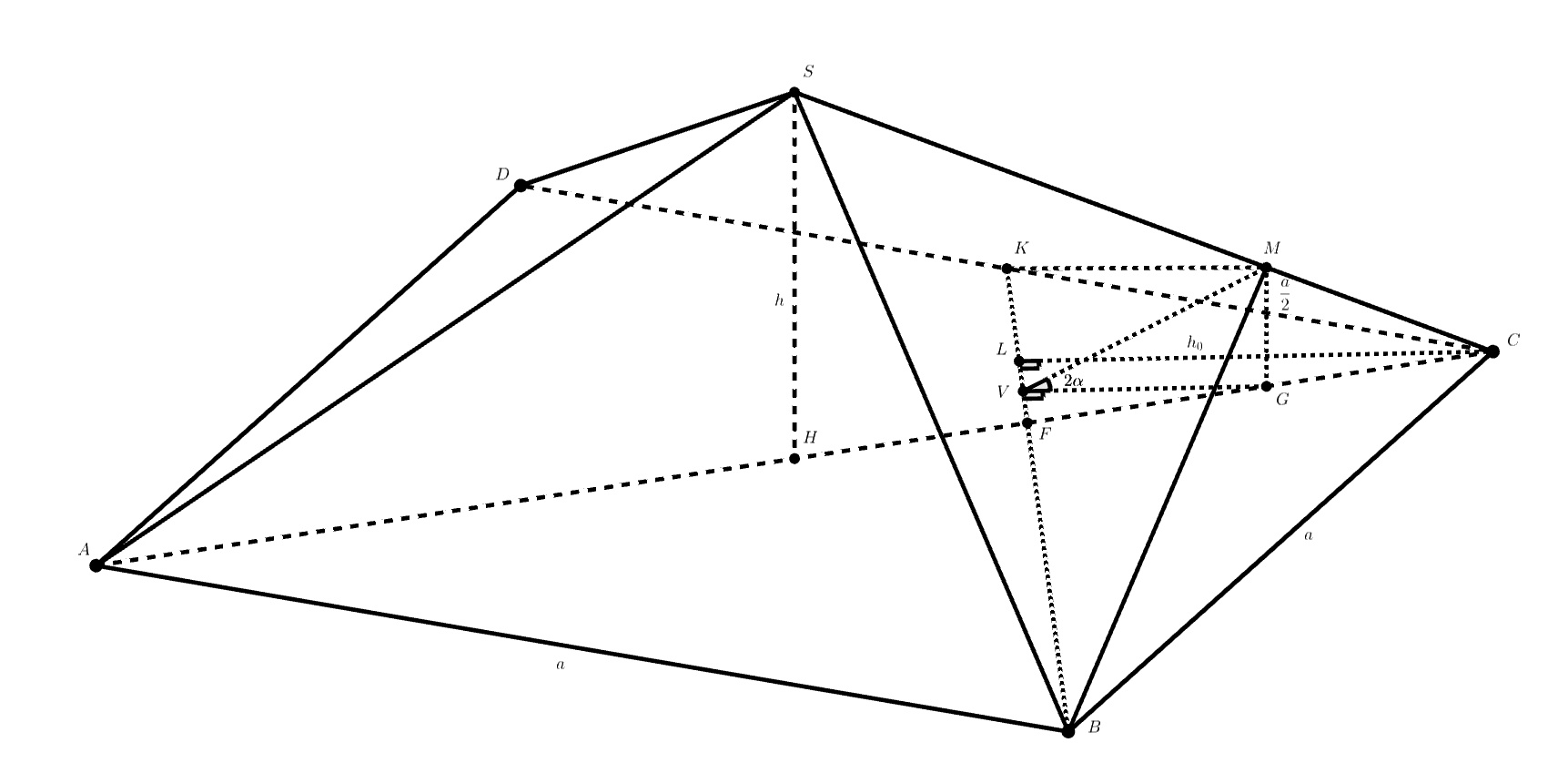
Тогда . Если
, то
— высота треугольника
проведенная из вершины
Ошибка.
Попробуйте повторить позже
В 2022 году исполняется 65 лет запуска первого искусственного спутника Земли (ИСЗ). В настоящее время для обеспечения бесперебойной работы сотовой связи, систем теле и радиовещания используются различные виды спутников, находящихся на различных орбитах, на различных высотах.
Зоной покрытия спутника назовем часть поверхности земного шара, в пределах которой обеспечивается уровень сигналов к спутнику и от него, необходимый для их приема с заданным качеством в конкретный момент времени. Как правило, эта часть поверхности ограничивается окружностью, проходящей по линии видимого горизонта. На рисунке линия проходит через точку Г:

a) Определите площадь земной поверхности ( ), которая является зоной покрытия спутника, находящегося на высоте
км
относительно земной поверхности, считая ее сферой радиуса
км с центром в точке
б) Найдите все значения для которых на поверхности земли можно расположить окружности
каждая из которых
внешним образом касается окружности
с центром в точке
и радиусом
каждая из них является границей зоны покрытия
ИСЗ, находящегося на той же высоте
, что и спутник с зоной покрытия
Каждая из зон покрытия
должна внешним образом
касаться окружностей
и
т.е. первая касается
и
вторая —
и
и т.д. Окружность
должна
касаться
и
Источники:
Пункт а, подсказка 1
Вспомним формулу площади шарового сегмента: S = 2πR*h, где h = АЗ. Осталось только найти h и посчитать
Пункт б, подсказка 1
Пусть В — точка касания C₀ и C₁, а З, З₁, З₂ — точки пересечения радиусов сферы, проходящих через центры окружностей. sin(а) можно найти из треугольника АВО. Заметим равенство углов ЗОВ и ВОЗ₁, что делает угол ЗОЗ₁ равным 2а. Найдем ЗЗ₁ через равенство треугольников ОГВ и ОЗ₁З(по двум сторонам и углу). Как нам связать это с количеством окружностей?
Пункт б, подсказка 2
Через двугранный угол при ребре ОЗ. Он будет зависеть от количества таких окружностей и равняться 360°/n
Пункт б, подсказка 3
Чтобы его выразить, опустим перпендикуляры из точек З₁ и З₂ на ребро ОЗ. Пирамида ОЗЗ₁З₂ правильная, поэтому З₁Н и З₂Н пересекутся в одной точке Н и будут равны. Теперь нам нужно их найти.
Пункт б, подсказка 4
Рассмотрим треугольник З₂НЗ₁. Выразим З₂З₁, которую мы уже знаем, через З₁Н и половину угла З₂НЗ₁. Из уравнения выразим sin(180°/n). Осталось только его оценить и получить из этого оценку на n!

а) Зона покрытия — часть сферы, лежащая внутри конуса. , где
— высота сегмента.
, здесь угол
—
угол между радиусом ОГ и линией ОА, соединяющий центр сферы с центром окружности, которая является линией пересечения сферы и
конуса.
Тогда площадь равна
б) Пусть О — центр сферы, В — точка касания первой и второй окружности, А и их центры этих окружностей,
— точки
пересечения радиусов
со сферой. Обозначим
— угол между ОЗ и ОВ. Тогда

В правильной пирамиде О плоские углы при вершине равны
двугранный угол при ребре О3 равен
Опустив
перпендикуляры из точек
и
на ребро О3 в точку H, треугольники О
и О
равны (по трем сторонам), т.к. две стороны
равны
а третья

а)
б)

