ШВБ 2022

Поскольку пирамида правильная, то центр указанного шара лежит в плоскости , где — высота пирамиды. Пусть

Обозначим Проведем — точка касания шара плоскости пусть радиус шара

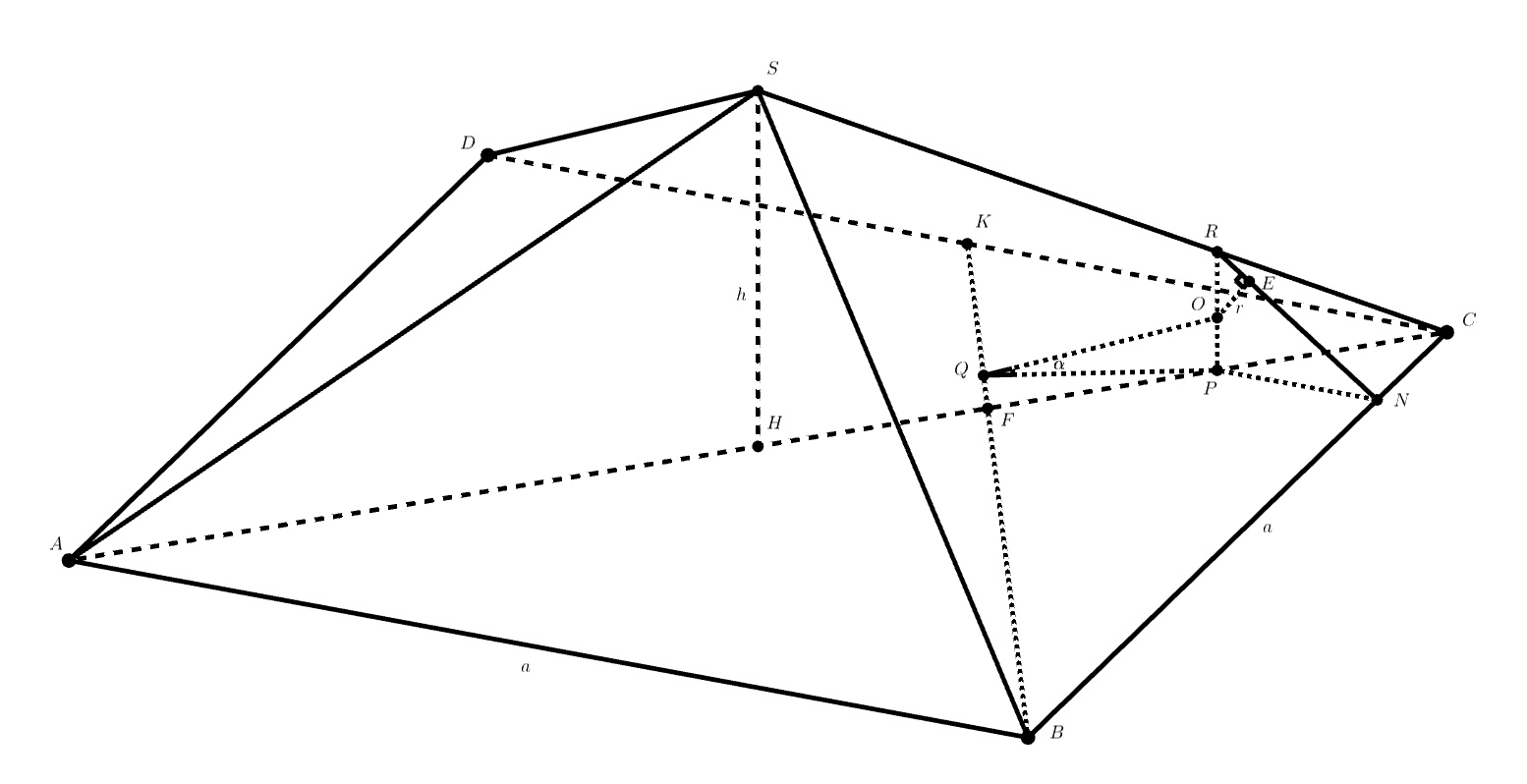
Поскольку то Треугольники и подобны, и или

По условию задачи Тогда

Точка — точка пересечения и тогда Поскольку

Пусть . Тогда Если то Угол между плоскостью и плоскостью основания равен Тогда

Пусть — отрезок перпендикуляра, опущенного из точки на плоскость основания , и .

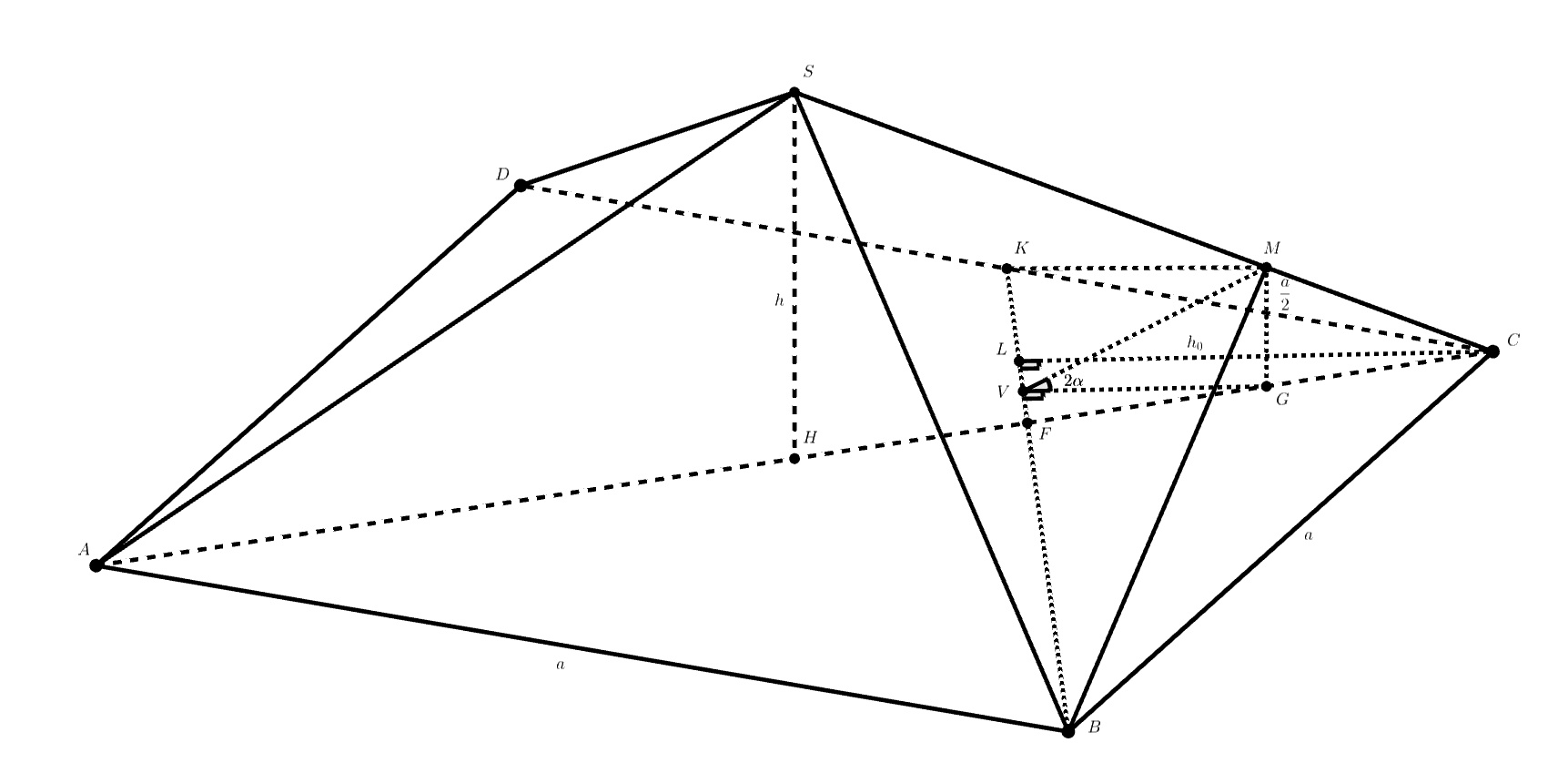
Тогда . Если , то

— высота треугольника проведенная из вершины