04 Прямая
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Как называется график линейной функции?
Источники:
Графиком линейной функции всегда является прямая.
Ошибка.
Попробуйте повторить позже
Что означает коэффициент в уравнении прямой
?
Источники:
Коэффициент определяет угол наклона прямой к оси
.
Ошибка.
Попробуйте повторить позже
Если как направлена прямая?
Источники:
При прямая возрастает, при
— убывает.
Ошибка.
Попробуйте повторить позже
Если как выглядит график функции?
Источники:
При уравнение принимает вид
— прямая, параллельная оси
.
Ошибка.
Попробуйте повторить позже
Если две прямые параллельны, то их угловые коэффициенты?
Источники:
Параллельные прямые имеют одинаковый наклон ().
Ошибка.
Попробуйте повторить позже
Даны две прямые: и
Каково их взаимное расположение?
Источники:
Угловые коэффициенты равны () но
То есть прямые параллельны.
Ошибка.
Попробуйте повторить позже
Найдите уравнение прямой, проходящей через точки и
Источники:
Способ
Наклон
Подставляем
и точку
в уравнение:
Способ
Уравнение прямой имеет вид:
- 1.
-
Прямая, проходящая через точку
имеет вид:
- 2.
-
Прямая, проходящая через точку
имеет вид:
- 3.
-
Так как это одна и та же прямая, проходящая через обе точки, то запишем систему уравнений:
- 4.
-
Решаем систему методом вычитания:
- 5.
-
Подставляем
в первое уравнение:
Ошибка.
Попробуйте повторить позже
Дана прямая . Какая прямая ей перпендикулярна?
А)
Б)
В)
Г)
Источники:
Условие перпендикулярности: Здесь
Ошибка.
Попробуйте повторить позже
На рисунке изображена прямая, проходящая через точки A и B. Найдите её уравнение.
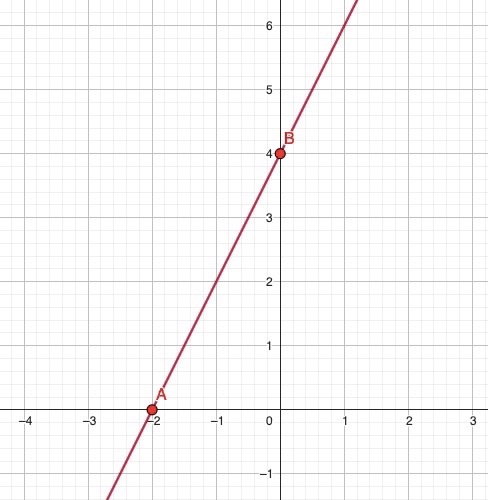
Источники:
Наклон
Пересечение с осью
:
Ошибка.
Попробуйте повторить позже
На рисунке прямая параллельна оси и проходит через точку
Запишите её уравнение.
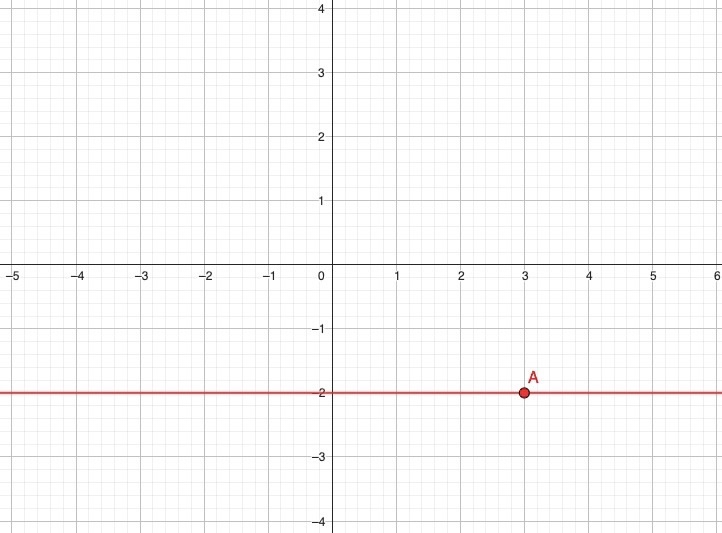
Источники:
Горизонтальная прямая имеет вид Здесь
Ошибка.
Попробуйте повторить позже
Постройте график функции:
Источники:
- 1.
-
Для
:
- Найдём точку пересечения с осью
: при
,
→
- Вторая точка: при
,
→
- Строим прямую через эти точки:
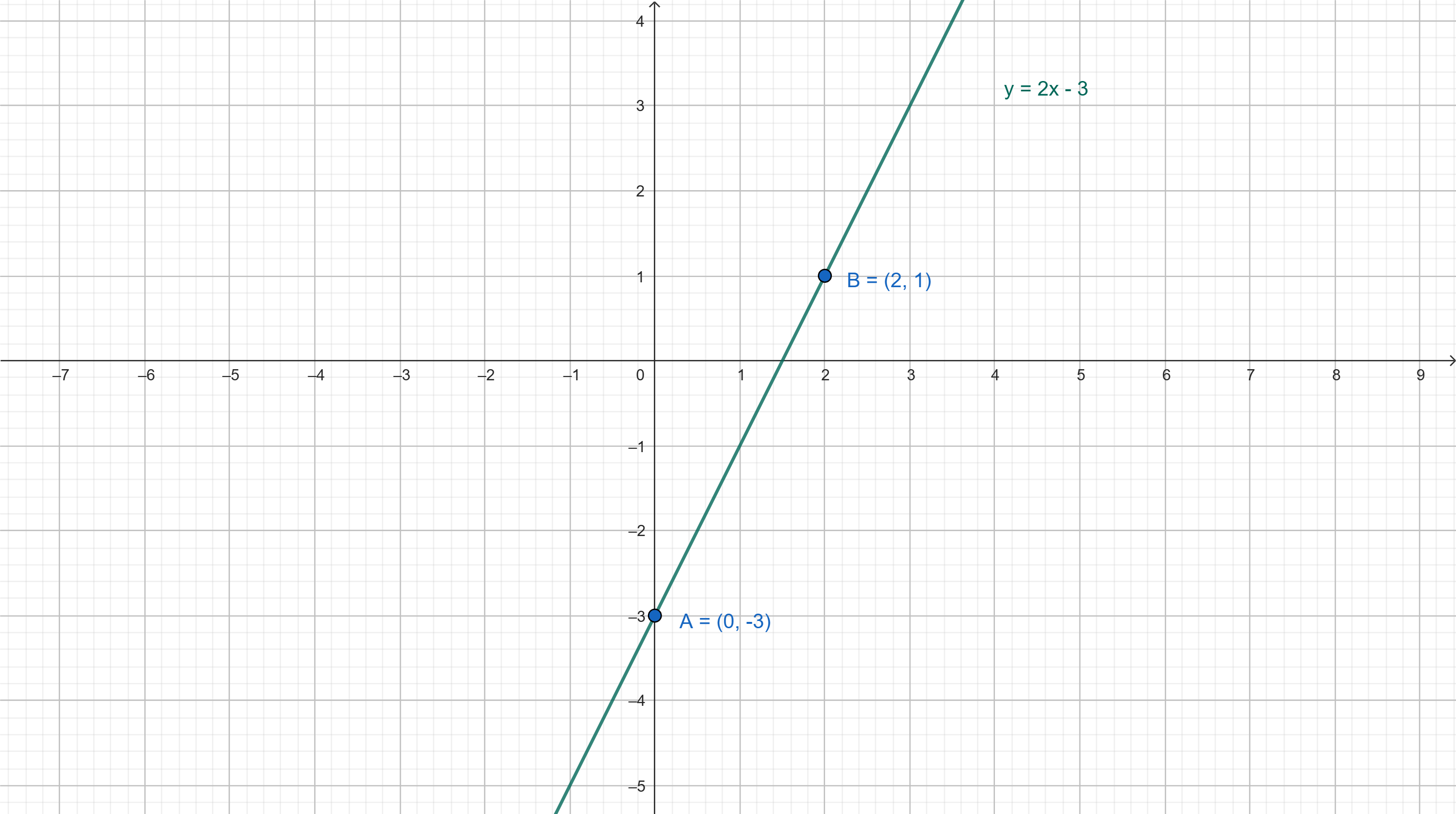
- Найдём точку пересечения с осью
- 2.
-
Для
:
- Точка пересечения с
:
- Вторая точка: при
,
→
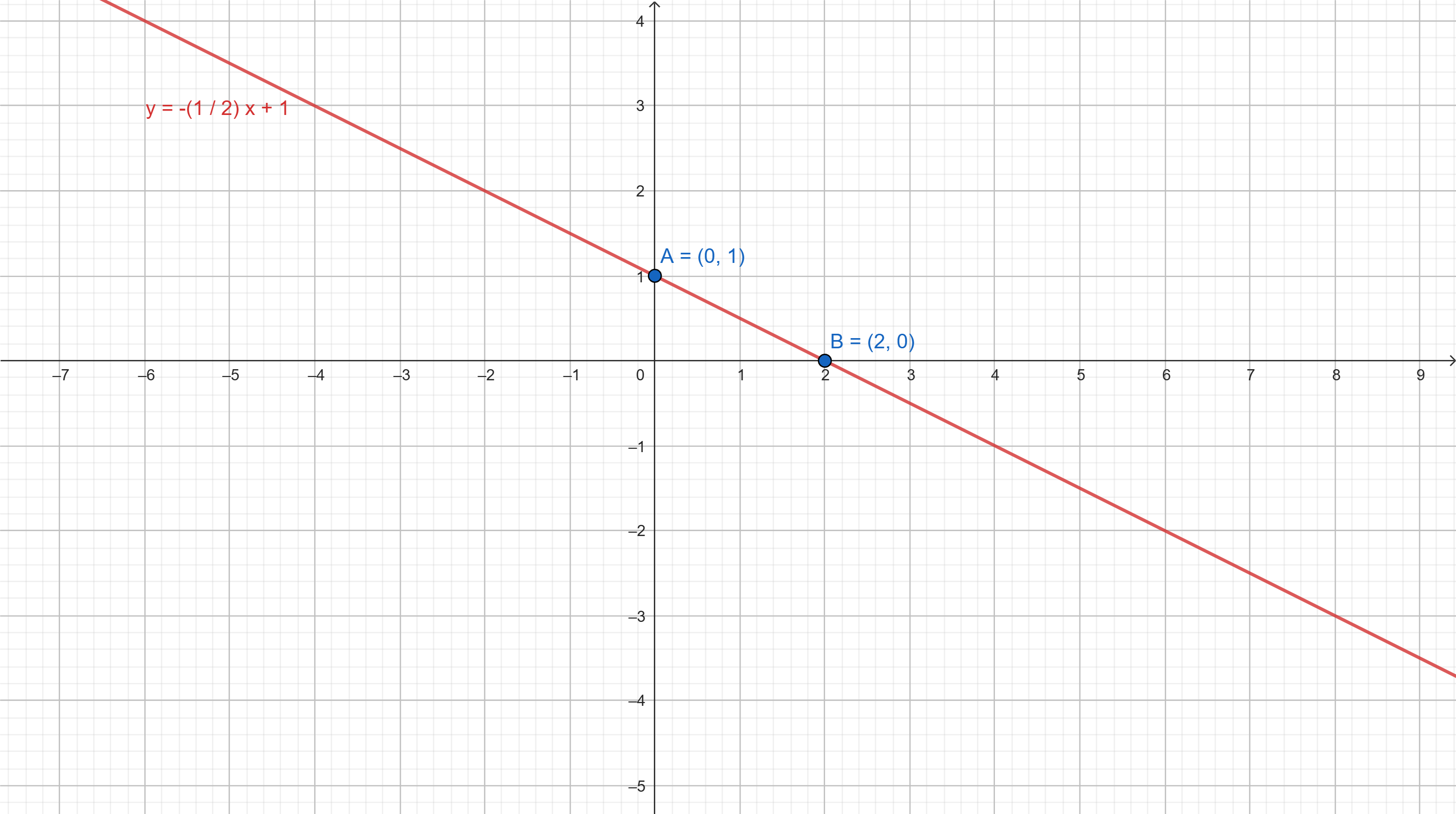
- Точка пересечения с
Ошибка.
Попробуйте повторить позже
График функции проходит через точку
Найдите
Источники:
Подставляем координаты точки в уравнение:
Ошибка.
Попробуйте повторить позже
Прямая проходит через точки
и
Найдите
и
Источники:
- 1.
-
Подставляем первую точку
- 2.
-
Подставляем вторую точку
при
Ошибка.
Попробуйте повторить позже
Найдите уравнение прямой, параллельной и проходящей через точку
Источники:
Исходная прямая имеет
У параллельной прямой (по условию параллельности)
Общий вид искомой прямой:
Подставляем координаты точки
Ошибка.
Попробуйте повторить позже
При каком прямые
и
параллельны?
Источники:
Условие параллельности:
Ошибка.
Попробуйте повторить позже
Даны прямые:
Найдите все значения при которых эти прямые:
а) Параллельны
б) Перпендикулярны
Источники:
- 1.
-
Для параллельности:
Проверка на совпадение:
При
:
- 1-я прямая:
- 2-я прямая:
Разные
параллельны, но не совпадают
- 1-я прямая:
- 2.
-
Для перпендикулярности:
Ошибка.
Попробуйте повторить позже
Найдите точку пересечения и
Источники:
Ошибка.
Попробуйте повторить позже
Найдите уравнение прямой, проходящей через точки и
Источники:
Подставим первую точку в уравнение прямой
Подставим вторую точку:
Тогда уравнение прямой:
Ошибка.
Попробуйте повторить позже
Найти точку пересечения и
Источники:
Приравняем уравнения прямых
Ошибка.
Попробуйте повторить позже
Найдите уравнение прямой, перпендикулярной и проходящей через
Источники:
Исходная прямая имеет
У перпендикулярной прямой:
Общий вид искомой прямой:
Подставляем



