.05 Перебор
Ошибка.
Попробуйте повторить позже
Сколько существует чисел, больших, чем каждое из которых можно получить перестановкой цифр данного числа?
Источники:
Нам дано число Нужно найти количество перестановок его цифр, которые больше, чем
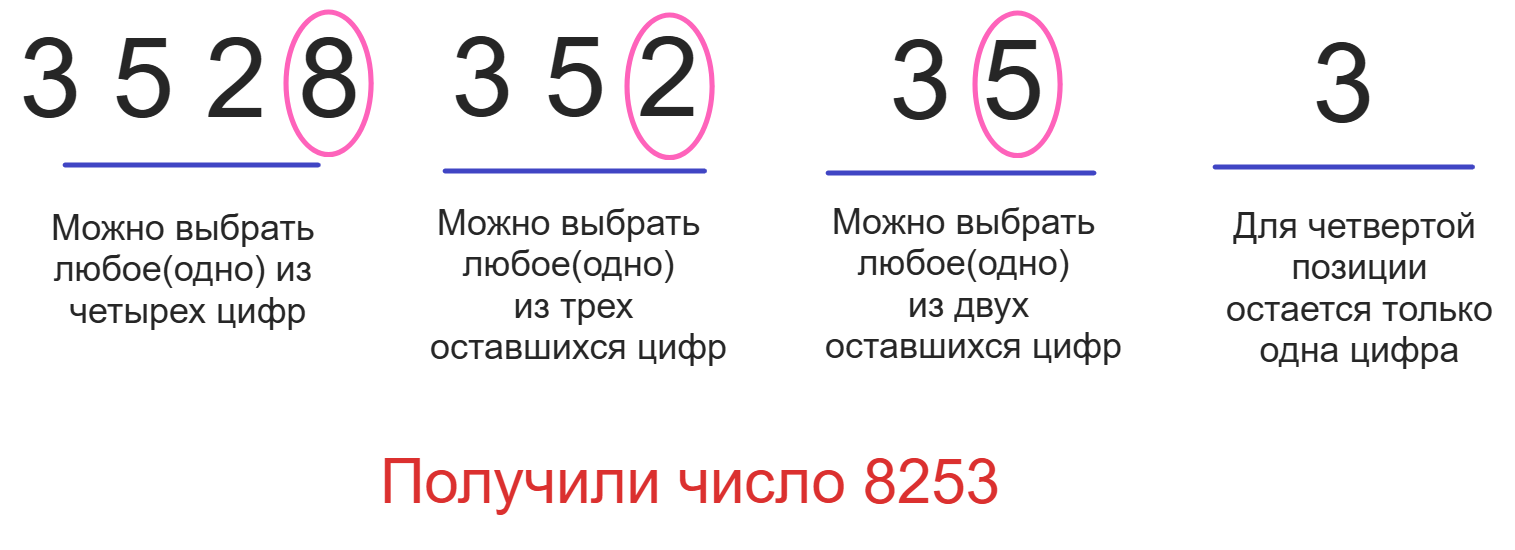
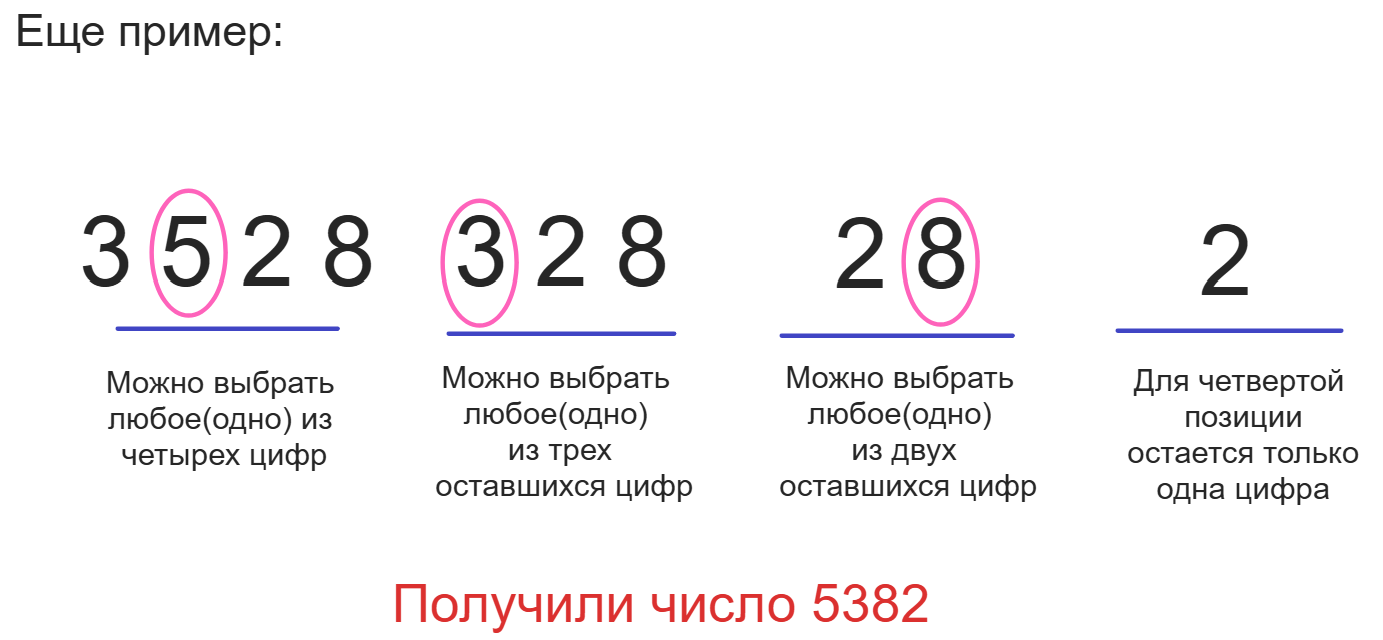
Получается, для первой позиции варианта из предложенных цифр, для второй позиции
варианта, для третьей -
для последней
-
Представьте, вы хотите раздать карточки друзьям, на каждой карточке нарисована какая-то цифра. Подходите к первому человеку,
на руках у вас
карточки, отдаете ему одну. Идете к следующему другу, заметьте, теперь у вас на руках только
карточки, из этих трех
вы выбираете одну и даете второму другу. Подходит третий: он выбирает одну карточку из двух предложенных. А для четвертого друга
остается только одна карточка. Здесь так же.
Получается вариантов всего. Часто такое умножение записывают как факториал числа:
(Еще пример:
Всего перестановок Перечислим их все, а затем отбросим те, что меньше или равны
Сначала упорядочим цифры по возрастанию:
Перестановки, начинающиеся с
Все меньше, чем
Перестановки, начинающиеся с
и
меньше,
равно.
Перестановки, начинающиеся с
Все больше, чем
Перестановки, начинающиеся с
Все больше, чем
Теперь посчитаем количество чисел, которые больше
Таким образом, существует чисел, больших, чем
каждое из которых можно получить перестановкой цифр данного
числа.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




