Тема №20-22 Механика

06 Задания СтатГрада

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела №20-22 механика

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#104779

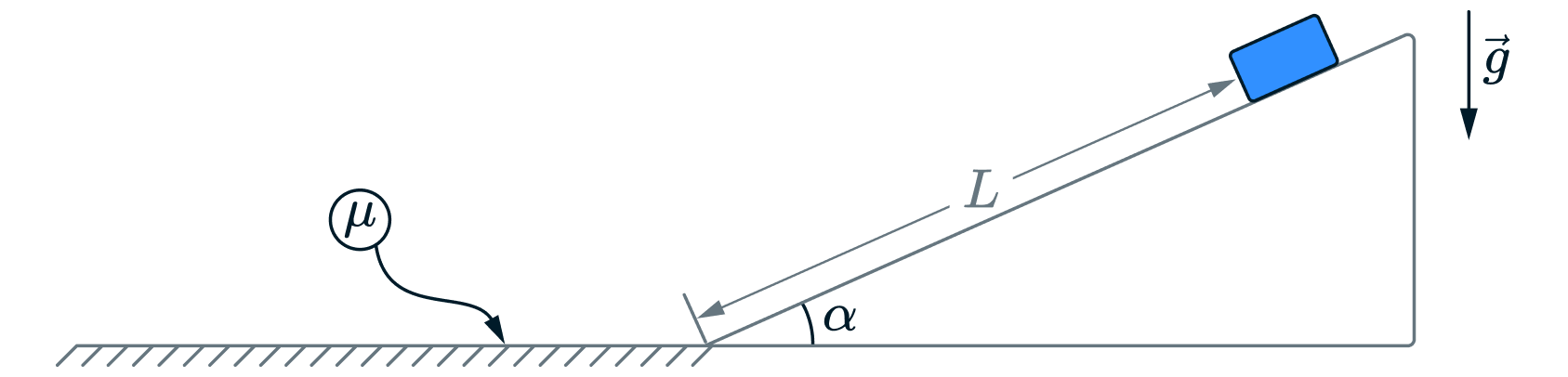
Небольшой брусок соскальзывает с гладкого закреплённого клина, наклонённого под углом $∘ α= 30$ к горизонту. Проехав по клину расстояние $L = 1$ м (см. рисунок), брусок плавно (без удара) переезжает на шероховатую поверхность с коэффициентом трения $μ =0,2$ . Какое расстояние проедет брусок по горизонтальной поверхности до полной остановки?

$PIC$

Источники: Статград 2025 декабрь №1 ОГЭ

Показать ответ и решение

Т.к. клин гладкий, то выполняется закон сохранения механической энергии. Высота нахождения начального положения бруска равна $H =Lsinα$ .
Тогда скорость в конце клина можно найти через ЗСМЭ

2 2 mgH = mvк-− mvн, (1) 2 2

где $m$ - масса бруска, $vк$ - конечная скорость бруска при движении по клину, $vн = 0 м/c$ - начальная скорость бруска.
Далее брусок движется по горизонтальному шероховатому участку. Понятно, что вся кинетическая энергия уйдет в тепло, выделяемое за счёт трения о поверхность. Тогда можно записать закон изменения кинетической энергии

2 2 mvк-− mvк2 =A тр, (2) 2 2

где $v2к2$ - конечная скорость движения( в нашем случае требуется рассмотреть движение до полной остановки, т.е. конечная скорость равна 0), $Aтр = μmgS$ - работа силы трения, $S$ - расстояние, которое пройдет брусок по шероховатой поверхности.
Тогда объединяя уравнения (1) и (2), получим

mgH = μmgS,

L ⋅sinα 1⋅0,5 S =---μ---= -0,2- =2,5 м.

Ответ:

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#104791

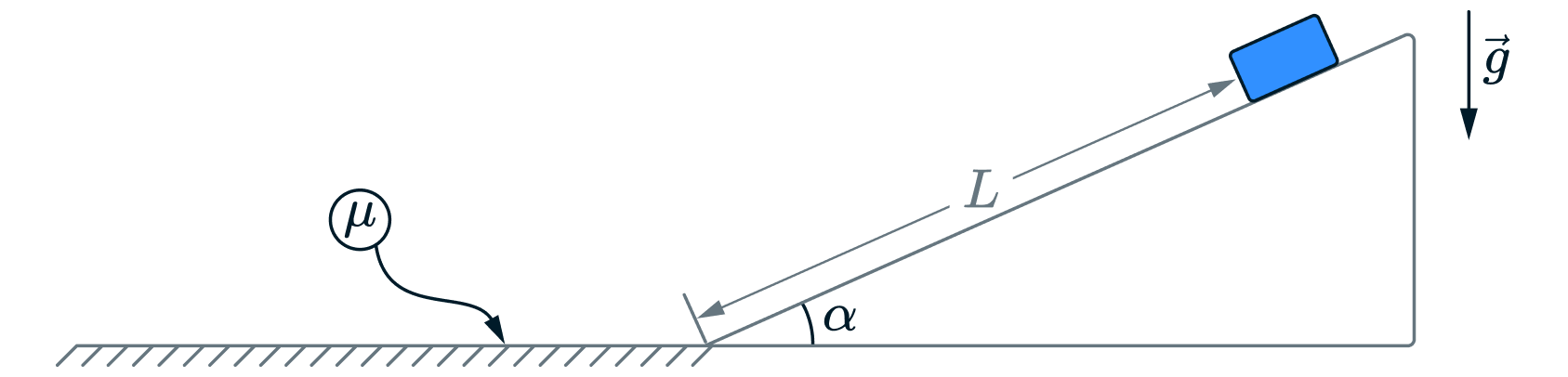
Небольшой брусок соскальзывает с гладкого закреплённого клина, наклонённого под углом $∘ α = 30$ к горизонту. Проехав по клину расстояние $L= 1$ м (см. рисунок), брусок плавно (без удара) переезжает на горизонтальную шероховатую поверхность и проезжает по ней расстояние 2 м до полной остановки. Вычислите коэффициент трения бруска о шероховатую поверхность.

$PIC$

Источники: Статград 2025 декабрь №2 ОГЭ

Показать ответ и решение

Т.к. клин гладкий, то выполняется закон сохранения механической энергии. Высота нахождения начального положения бруска равна $H =Lsinα$ .
Тогда скорость в конце клина можно найти через ЗСМЭ

2 2 mgH = mvк-− mvн, (1) 2 2

где $m$ - масса бруска, $vк$ - конечная скорость бруска при движении по клину, $vн = 0 м/c$ - начальная скорость бруска.
Далее брусок движется по горизонтальному шероховатому участку. Понятно, что вся кинетическая энергия уйдет в тепло, выделяемое за счёт трения о поверхность. Тогда можно записать закон изменения кинетической энергии

2 2 mvк-− mvк2 =A тр, (2) 2 2

где $v2к2$ - конечная скорость движения( в нашем случае требуется рассмотреть движение до полной остановки, т.е. конечная скорость равна 0), $Aтр = μmgS$ - работа силы трения, $S$ - расстояние, которое пройдет брусок по шероховатой поверхности.
Тогда объединяя уравнения (1) и (2), получим

mgH = μmgS,

Lsinα 1⋅0,5 μ= --S-- = --2--= 0,25.

Ответ:

Курсы

Всё необходимое для достижения цели

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания