.09 Задания СтатГрада
Ошибка.
Попробуйте повторить позже
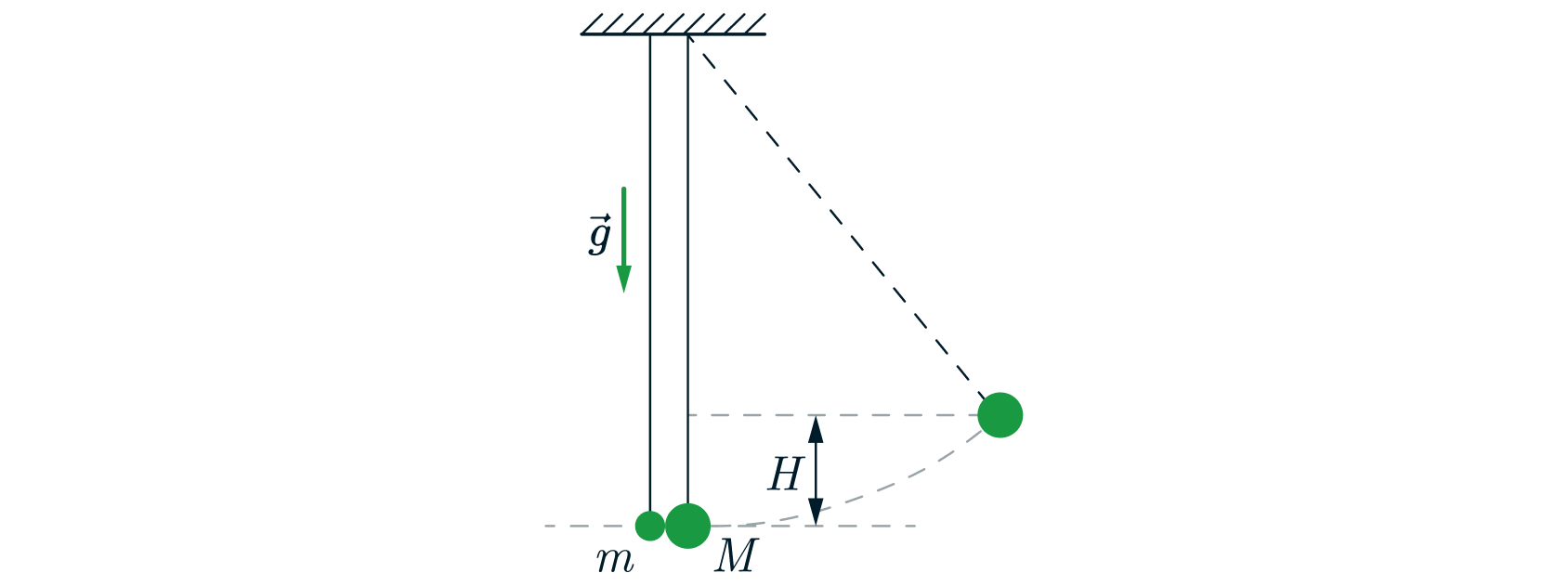
На штативе на двух тонких длинных вертикальных нерастяжимых нитях подвешены два абсолютно упругих маленьких шарика,
которые касаются друг друга на горизонтальной линии, проходящей через их центры (см. рисунок). Масса первого шарика равна
г, масса второго шарика
г. Первый шарик отклоняют в плоскости нитей так, что он поднимается на высоту
см, и отпускают без начальной скорости. На какую максимальную высоту
поднимется второй шарик после первого
столкновения с первым шариком?
Источники:
По закону сохранения для шарика
где - скорость перед столкновением. Поскольку на шарики не действуют диссипативные силы вдоль горизонтальной оси, то по
закону сохранения импульса и по закону сохранения энергии
где - скорость шарика
после столкновения;
- скорость шарика
после столкновения.
После соударения шарик поднимется на высоту
, определяемую с помощью закона сохранения энергии
Решая систему из (1) и (2), получим
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




