09 Задания СтатГрада
Ошибка.
Попробуйте повторить позже
На невесомой нерастяжимой нити длиной см, привязанной наверху к неподвижному крючку, подвешен маленький шарик
массой
г. Снизу к шарику прикреплена лёгкая пружина жёсткостью
Н/м, растянутая на
см до длины,
равной длине нити
, причем нижний конец пружины находится точно под крючком и заделан в неподвижном основании. Шарик
оттягивают в горизонтальном направлении на малое расстояние
и отпускают. Найдите частоту
возникающих после этого
колебаний, пренебрегая потерями на трение.
Источники:
Изобразим систему на рисунке и силы, действующие на шарик при его отклонении.
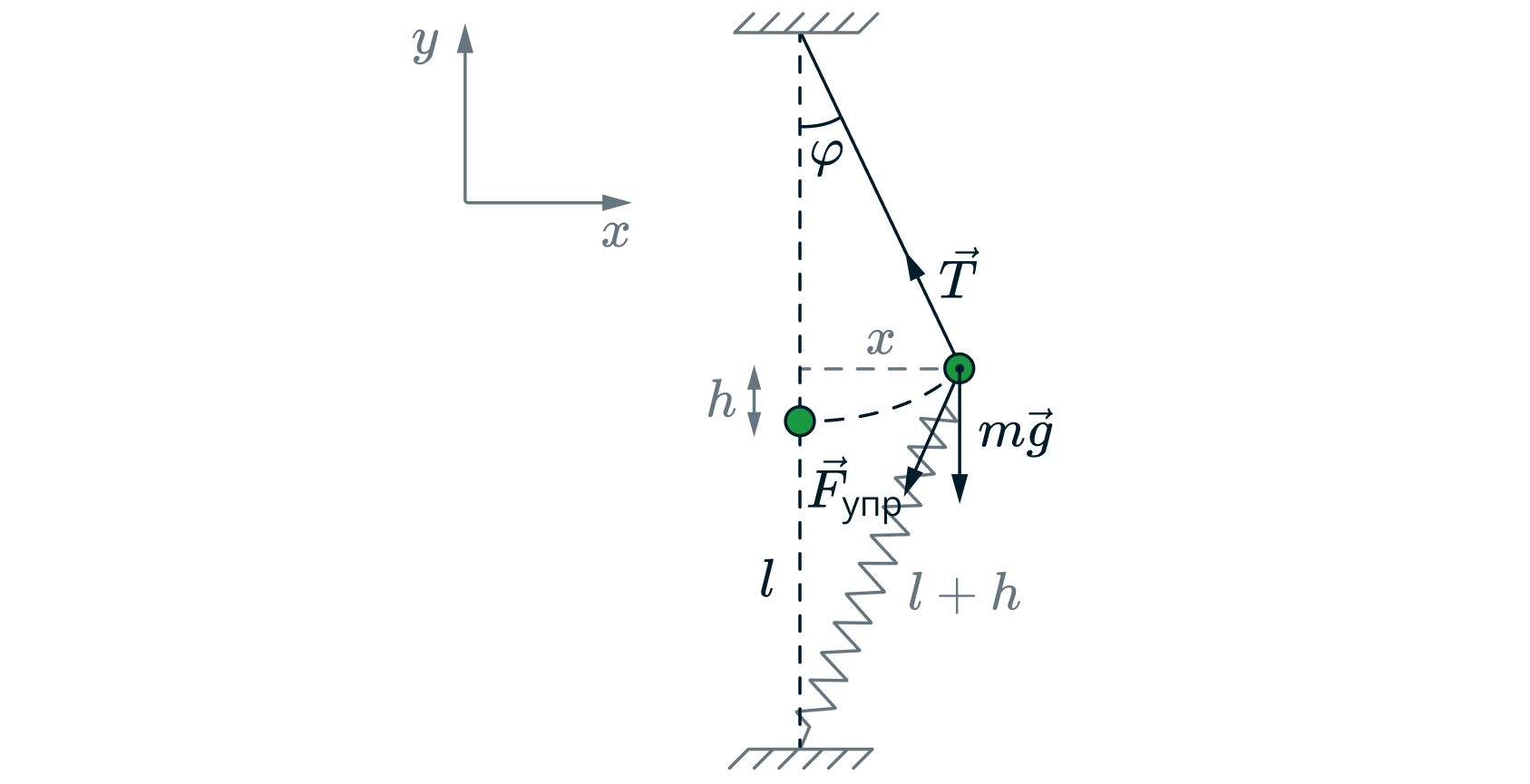
В силу нерастяжимости нити шарик двигался по дуге окружности с радиусом . Пусть высота, на которую поднялся шарик,
равна
. Поскольку отклонение мало по сравнению с длиной пружины, можно считать, что она удлинилась на
.
По теореме Пифагора
Поскольку , то тем более
. Тогда
Следовательно, верткальным смещением шарика можно пренебречь по сравнению с горизонтальным смещение. Значит, можно
считать, что ,как и в равновесном состоянии, верткальные силы уравновешены.
Запишем второй закон Ньютона,с учетом вышеописанных допущений, в проекции на ось
где - сила упругости;
- угол отклонения нити.
Поскольку из геометрии рисунка видно, что , то
и
.
Тогда получаем
Запишем второй закон Ньютона,с учетом вышеописанных допущений, в проекции на ось
Ошибка.
Попробуйте повторить позже
На невесомой нерастяжимой нити длиной см, привязанной наверху к неподвижному крючку, подвешен маленький шарик
массой
г. Снизу к шарику прикреплена лёгкая пружина жёсткостью
Н/м, растянутая на
см до длины,
равной длине нити
, причем нижний конец пружины находится точно под крючком и заделан в неподвижном основании. Шарик
оттягивают в горизонтальном направлении на малое расстояние
и отпускают. Найдите частоту
возникающих после этого
колебаний, пренебрегая потерями на трение.
Источники:
Изобразим систему на рисунке и силы, действующие на шарик при его отклонении.
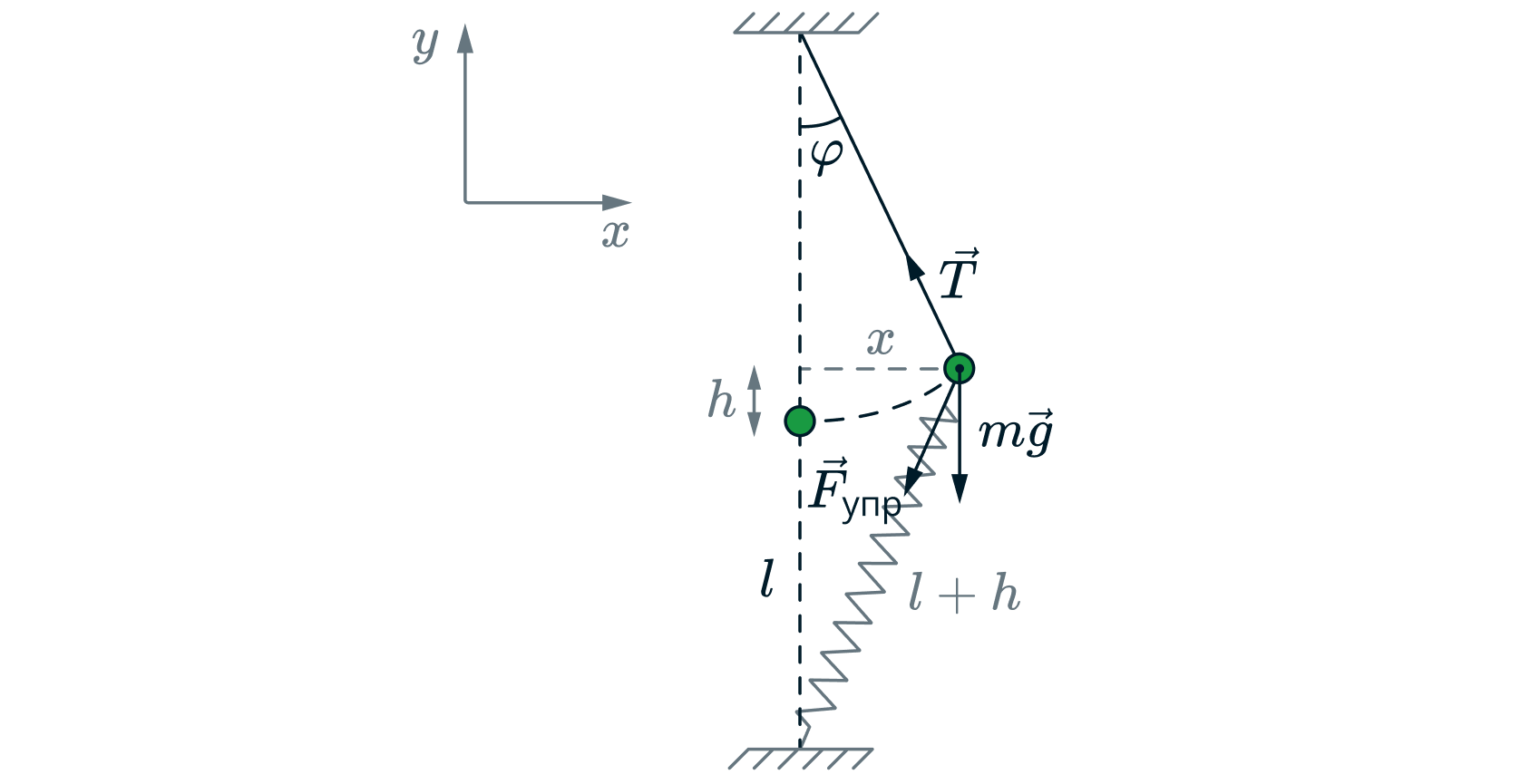
В силу нерастяжимости нити шарик двигался по дуге окружности с радиусом . Пусть высота, на которую поднялся шарик,
равна
. Поскольку отклонение мало по сравнению с длиной пружины, можно считать, что она удлинилась на
.
По теореме Пифагора
Поскольку , то тем более
. Тогда
Следовательно, верткальным смещением шарика можно пренебречь по сравнению с горизонтальным смещение. Значит, можно
считать, что ,как и в равновесном состоянии, верткальные силы уравновешены.
Запишем второй закон Ньютона,с учетом вышеописанных допущений, в проекции на ось
где - сила упругости;
- угол отклонения нити.
Поскольку из геометрии рисунка видно, что , то
и
.
Тогда получаем
Запишем второй закон Ньютона,с учетом вышеописанных допущений, в проекции на ось
Ошибка.
Попробуйте повторить позже
Школьник, изучая механические колебания, изготовил два маятника – математический с периодом малых колебаний c и
пружинный с периодом колебаний
. Второй маятник был подвешен в вертикальном положении за свободный конец
пружины. Найдите деформацию
пружины для второго маятника в состоянии равновесия.
Источники:
Приведем формулы для периодов колебаний математического и пружинного маятников
где - длина маятника;
- ускорение свободного падения.
где - масса груза;
- жёсткость пружины.
Из равенства (2) следует
Запишем второй закон Ньютона для установившегося состояния второго маятника
Из (1) следует, что
Тогда
Ошибка.
Попробуйте повторить позже
Школьник, изучая механические колебания, изготовил два маятника – математический с периодом малых колебаний c и
пружинный с периодом колебаний
. Второй маятник был подвешен в вертикальном положении за свободный конец
пружины. Найдите деформацию
пружины для второго маятника в состоянии равновесия.
Источники:
Приведем формулы для периодов колебаний математического и пружинного маятников
где - длина маятника;
- ускорение свободного падения.
где - масса груза;
- жёсткость пружины.
Из равенства (2) следует
Запишем второй закон Ньютона для установившегося состояния второго маятника
Из (1) следует, что
Тогда
Ошибка.
Попробуйте повторить позже
Школьник сел в электробус, чтобы доехать до школы. На улице накрапывал дождик, но на вертикальные лобовые стекла кабины
водителя капли во время остановки не попадали. Когда электробус тронулся и начал ускоряться, на лобовые стекла кабины капли
дождя стали попадать, и тем чаще, чем выше становилась скорость электробуса, что заставляло водителя периодически включать
«дворники». Сколько капель дождя попало на эти стекла за время с равноускоренного разгона электробуса от остановки до
скорости
км/ч, если площадь стекол равна
м2, а концентрация капель в воздухе составляла
м-3? Можно считать, что до столкновения со стеклом кабины скорость капель остаётся такой же, как и вдалеке от
электробуса.
Источники:
Число капель, попадающих на стекла кабины за малый промежуток времени
, равно произведению их концентрации на
объём слоя воздуха, захватываемый стеклом электробуса. Этот объем равен
где - скорость электробуса в малом промежутке времени.
Тогда
где .
Таким образом, полное число капель, попавших на стекла, равно
где - полный путь электробуса.
Для равноускоренного движения от 0 скорости до полный путь равен
Получаем окончательно
Ошибка.
Попробуйте повторить позже
Школьник сел в электробус, чтобы доехать до школы. На улице накрапывал дождик, но на вертикальные лобовые стекла кабины
водителя капли во время остановки не попадали. Когда электробус тронулся и начал ускоряться, на лобовые стекла кабины капли
дождя стали попадать, и тем чаще, чем выше становилась скорость электробуса, что заставляло водителя периодически включать
«дворники». До какой скорости разогнался электробус за время
с при равноускоренном движении от остановки, если за
время разгона на лобовые стекла попало
капель дождя, площадь стекол равна
м2, а концентрация капель в
воздухе составляла
м-3? Можно считать, что до столкновения со стеклом кабины скорость капель остаётся такой же, как и
вдалеке от электробуса.
Источники:
Число капель, попадающих на стекла кабины за малый промежуток времени
, равно произведению их концентрации на
объём слоя воздуха, захватываемый стеклом электробуса. Этот объем равен
где - скорость электробуса в малом промежутке времени.
Тогда
где .
Таким образом, полное число капель, попавших на стекла, равно
где - полный путь электробуса.
Для равноускоренного движения от 0 скорости до полный путь равен
Получаем окончательно
Выразим скорость
Ошибка.
Попробуйте повторить позже
Для приготовления домашнего мороженого мама школьника использовала следующий способ. Она заморозила в морозильнике до
температуры °С фруктовый сок, и далее при помощи блендера превращала кубики льда в «кашицу», состоящую
на
% из мелких ледяных частиц и на
% жидкого сока, находящуюся при температуре
°С. Какую массу m такого «мороженого» она могла получить за время
мин работы блендера мощностью
Вт, если
этой мощности расходовалась на обработку смеси и доведение её до конечного состояния?
Свойства жидкого сока считайте близкими к свойствам воды, теплообменом смеси с окружающими телами можно
пренебречь.
Источники:
Из условия следует, что механическая энергия, равная , потраченная на обработку льда, превращается во
внутреннюю энергия нагревания всей массы льда
от
до
и дальнейшем плавлении части массы льда
при
.
Запишем уравнение теплового баланса
где - удельная теплоемкость льда;
- удельная теплота плавления льда.
Тогда масса получившегося мороженого равна
Ошибка.
Попробуйте повторить позже
Для приготовления домашнего мороженого мама школьника использовала следующий способ. Она заморозила в морозильнике до
температуры °С фруктовый сок, и далее при помощи блендера превращала кубики льда в «кашицу», состоящую на
% из мелких ледяных частиц и на
% жидкого сока, находящуюся при температуре
°С. Какой объём
такого «мороженого» она могла получить за время
мин работы блендера мощностью
Вт, если
этой
мощности расходовалась на обработку смеси и доведение её до конечного состояния? Средняя плотность полученного мороженого
г/см3, свойства жидкого сока считайте близкими к свойствам воды, теплообменом смеси с окружающими телами можно
пренебречь.
Источники:
Из условия следует, что механическая энергия, равная , потраченная на обработку льда, превращается во
внутреннюю энергия нагревания всей массы льда
от
до
и дальнейшем плавлении части массы льда
при
.
Запишем уравнение теплового баланса
где - удельная теплоемкость льда;
- удельная теплота плавления льда.
Тогда масса получившегося мороженого равна
А объем, получившегося мороженого, равен
Ошибка.
Попробуйте повторить позже
На штативе на двух тонких длинных вертикальных нерастяжимых нитях подвешены два абсолютно упругих маленьких шарика,
которые касаются друг друга на горизонтальной линии, проходящей через их центры (см. рисунок). Масса первого шарика равна
г, масса второго шарика
г. Первый шарик отклоняют в плоскости нитей так, что он поднимается на высоту
см, и отпускают без начальной скорости. На какую максимальную высоту
поднимется второй шарик после первого
столкновения с первым шариком?
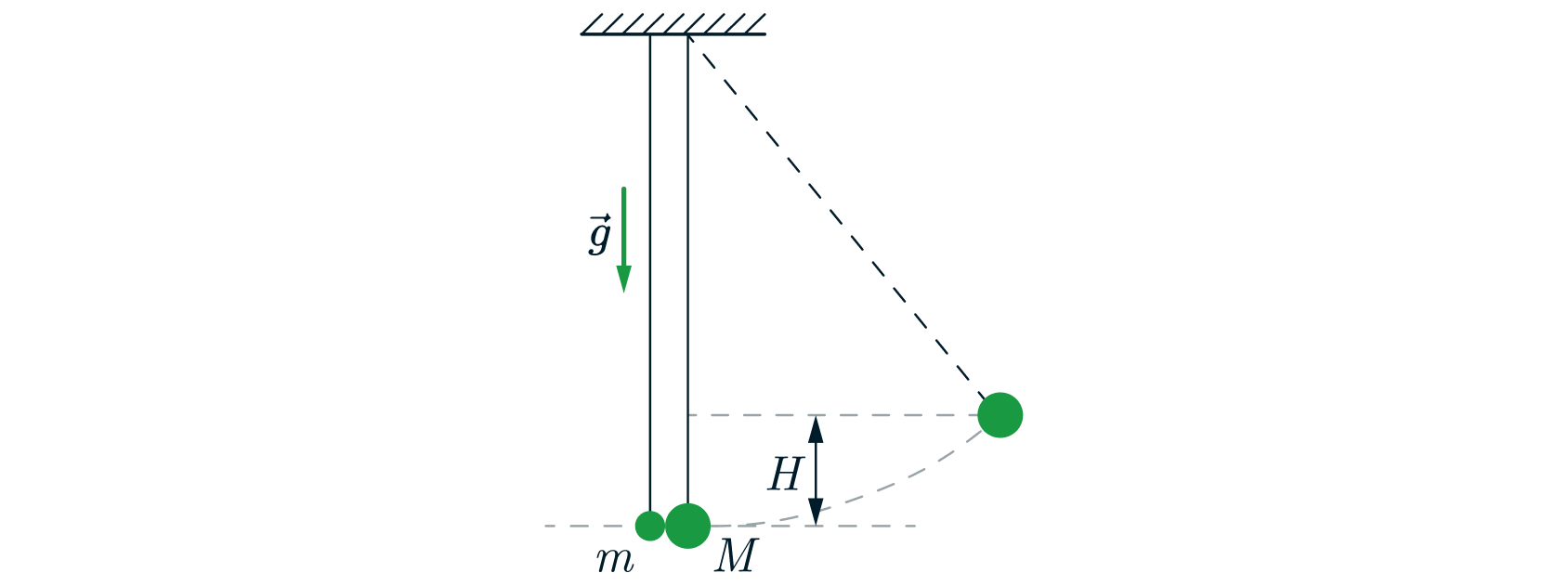
Источники:
По закону сохранения для шарика
где - скорость перед столкновением. Поскольку на шарики не действуют диссипативные силы вдоль горизонтальной оси, то по
закону сохранения импульса и по закону сохранения энергии
где - скорость шарика
после столкновения;
- скорость шарика
после столкновения.
После соударения шарик поднимется на высоту
, определяемую с помощью закона сохранения энергии
Решая систему из (1) и (2), получим
Ошибка.
Попробуйте повторить позже
На штативе на двух тонких длинных вертикальных нерастяжимых нитях подвешены два абсолютно упругих маленьких шарика,
которые касаются друг друга на горизонтальной линии, проходящей через их центры (см. рисунок). Масса первого шарика равна
г, масса второго шарика
г. Первый шарик отклоняют в плоскости нитей так, что он поднимается на высоту
см, и отпускают без начальной скорости. На какую максимальную высоту
поднимется первый шарик после первого
столкновения со вторым шариком?
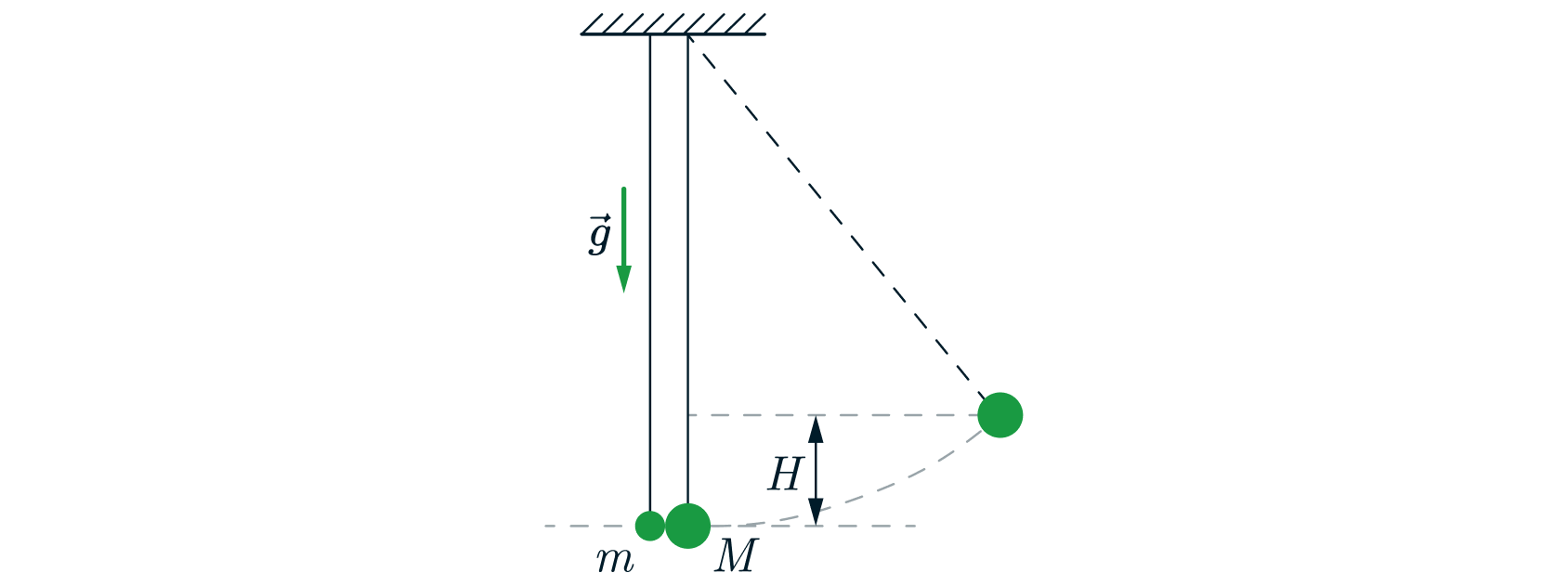
Источники:
По закону сохранения для шарика
где - скорость перед столкновением. Поскольку на шарики не действуют диссипативные силы вдоль горизонтальной оси, то по
закону сохранения импульса и по закону сохранения энергии
где - скорость шарика
после столкновения;
- скорость шарика
после столкновения.
После соударения шарик поднимется на высоту
, определяемую с помощью закона сохранения энергии
Решая систему из (1) и (2), получим


