.05 Задания СтатГрада
Ошибка.
Попробуйте повторить позже
В закрытый теплопроводящий цилиндр объёмом л с гладкими внутренними стенками вставлен тонкий тяжёлый поршень,
находящийся вначале, при горизонтальном положении цилиндра, около его левой крышки. Внутренний объём цилиндра сообщается
с сухим атмосферным воздухом, находящимся при нормальных условиях, через тонкую трубку с открытым краном, который может
отсоединять цилиндр от атмосферы. В исходном положении поршень находится чуть левее отверстия трубки (см. рисунок).
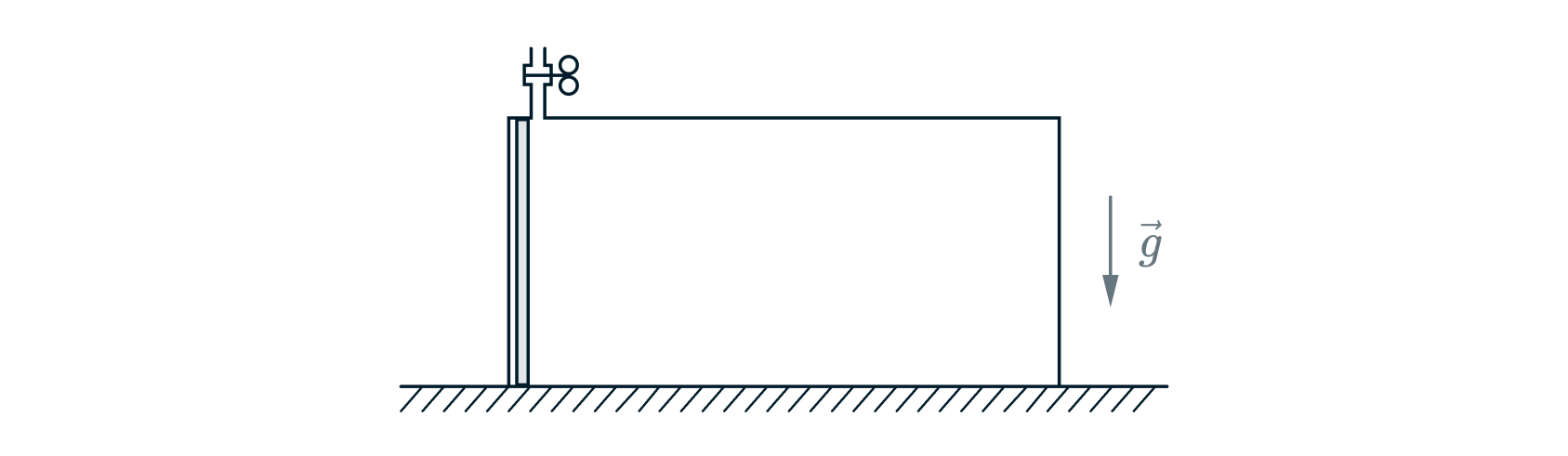
В некоторый момент цилиндр ставят в вертикальное положение с поршнем наверху, который опускается вниз, сразу перекрывая трубку
и сжимая воздух под собой, а после установления равновесия находится на высоте над дном цилиндра (высота цилиндра
м). Затем кран перекрывают и снова кладут цилиндр горизонтально. На какое расстояние
сдвинется поршень после
нового установления равновесия?
Источники:
Поскольку цилиндр теплопроводящиий, то можем считать, что во всех равновесных состояниях системы её температура постоянная
и равна температуре при нормальных условиях, то есть, K =
°С.
В первом состоянии весь цилиндр заполнен воздухом. Поскольку кран открыт, то давление газа в цилиндре равно атмосферному
Па.
Запишем уравнение Мендеелева-Клайперона
После поворота цилиндра в вертикальное положение, как следует из условия, объем газа уменьшился в 2 раза. Поскольку процесс изотермический, то давление увеличилось в 2 раза. Рассмотрим уравнение Мендеелева-Клайперона для верхней половины цилиндра
После кран закрыли и положи цилиндр горизонтально. Поскольку кран закрыт, то количества вещества в обеих частях сосуда
остается постоянным в течении всего процесса установления равновесия. Равновесия достигается при условии равенства давления
газов с двух сторон от поршня. Пусть при установлении равновесия длина правой части станет , а левой, соответственно,
.
Тогда уравнение Мендлеева-Клайперона для двух частей цилиндра будет выглядить следующим образом
Выразив и приравняв, получим
Тогда расстояние на которое сдвинется поршень равно
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




