Всесиб 2020

Предположим, что это не так, то есть каждый школьник был не более, чем на занятиях. Тогда по принципу Дирихле на одном из них он встретил хотя бы школьников (оставшихся школьников ). Пусть это было занятие по математике. По условию на нём были не все школьники, поэтому также найдётся такой, который на нём отсутствовал (назовём его Вася). Вася должен встретить всех школьников (которых как минимум ) с математики на других занятиях. Но раз между собой математики уже виделись, то встречи между ними произошли на разных восьми занятиях. Вася должен быть на всех. Получаем противоречие с тем, что каждый был не более, чем на семи занятиях.

Очевидно, что каждый факториал кратен При этом и делятся на откуда все кратны Но тогда должно делиться на что неверно, поскольку

Разобьём доску на квадратики клетки. Ввиду того, что никакие три отмеченные клетки не образуют трёхклеточный уголок, каждый такой квадратик содержит не более двух отмеченных клеток. Если две отмеченные в нём клетки — соседние по стороне, то разобьём его на два домино линией сетки, содержащей эту сторону. В случаях, когда в квадратике отмеченные клетки не соседние, или их не больше одной, разбиваем его на домино произвольным способом, скажем, на горизонтальные. Разбив указанным образом каждый квадратик, получим разбиение доски на домино, содержащие не более одной отмеченной клетки каждое.

Сделаем следующие действия: Разложим каждую разность на множители и получим:

Из получаем поэтому из имеем Из и получаем откуда Подставим найденные выражения в и и получим откуда Таким образом, получаем единственное решение системы:

Предположим, указанное в условии разбиение возможно. Сумма всех чисел от до равна следовательно, сумма чисел во множестве с максимальной суммой не меньше поэтому оно содержит не меньше чисел. По условию, каждое из девяти оставшихся множеств содержит различное, большее шести, количество чисел. Следовательно, во всех десяти множествах содержится не меньше чисел — противоречие.

Первое решение.

Горизонтальный отрезок длины с концами на графике функции существует тогда и только тогда, когда уравнение имеет при данном значении параметра хотя бы одно решение.

Раскрывая скобки, приводя подобные и сокращая на , получим квадратное уравнение , которое разрешимо при , откуда .

Следовательно, длина искомого отрезка не превосходит 2.

При решением уравнения является , откуда следует, что длина 2 достигается для отрезка с концами и на графике функции .

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Как в решении 1, получаем уравнение , которое рассмотрим как квадратное относительно с параметром :

ввиду положительности рассматриваем только тот, что с плюсом:

Данная функция от определена при и положительна при . Её производная

обращается в ноль при , слева больше ноля, а справа — меньше. Следовательно, её значение максимально при и равно . Действительно, в данном случае отрезок длины 2 соединяет на оси два корня и уравнения .

Первое решение.

Величина угла равна . Если бы луч лежал бы вне угла величина угла равнялась бы сумме величин и и была бы больше градусов, что противоречит условию. Следовательно, луч лежит внутри угла поэтому величина угла равна сумме величин углов и то есть градусам. Значит, угол — прямой и треугольник является прямоугольным с гипотенузой AC , а точка O середина стороны AC.

Обозначим точку пересечения биссектрисы со стороной за Углы и равны следовательно, прямые и симметричны относительно биссектрисы то же самое верно и для прямых и Значит, треугольники и равны и точки и симметричны относительно а треугольник прямоугольный равнобедренный.

Продлим отрезок до пересечения со стороной в точке симметричной относительно биссектрисы Обозначим за середину отрезка по теореме обратной теореме Фалеса отрезки и параллельны, следовательно угол равен углу то есть градусам. Значит, треугольник — прямоугольный равнобедренный и равен треугольникам и Отсюда следует, что точки и делят отрезок на три одинаковых части.

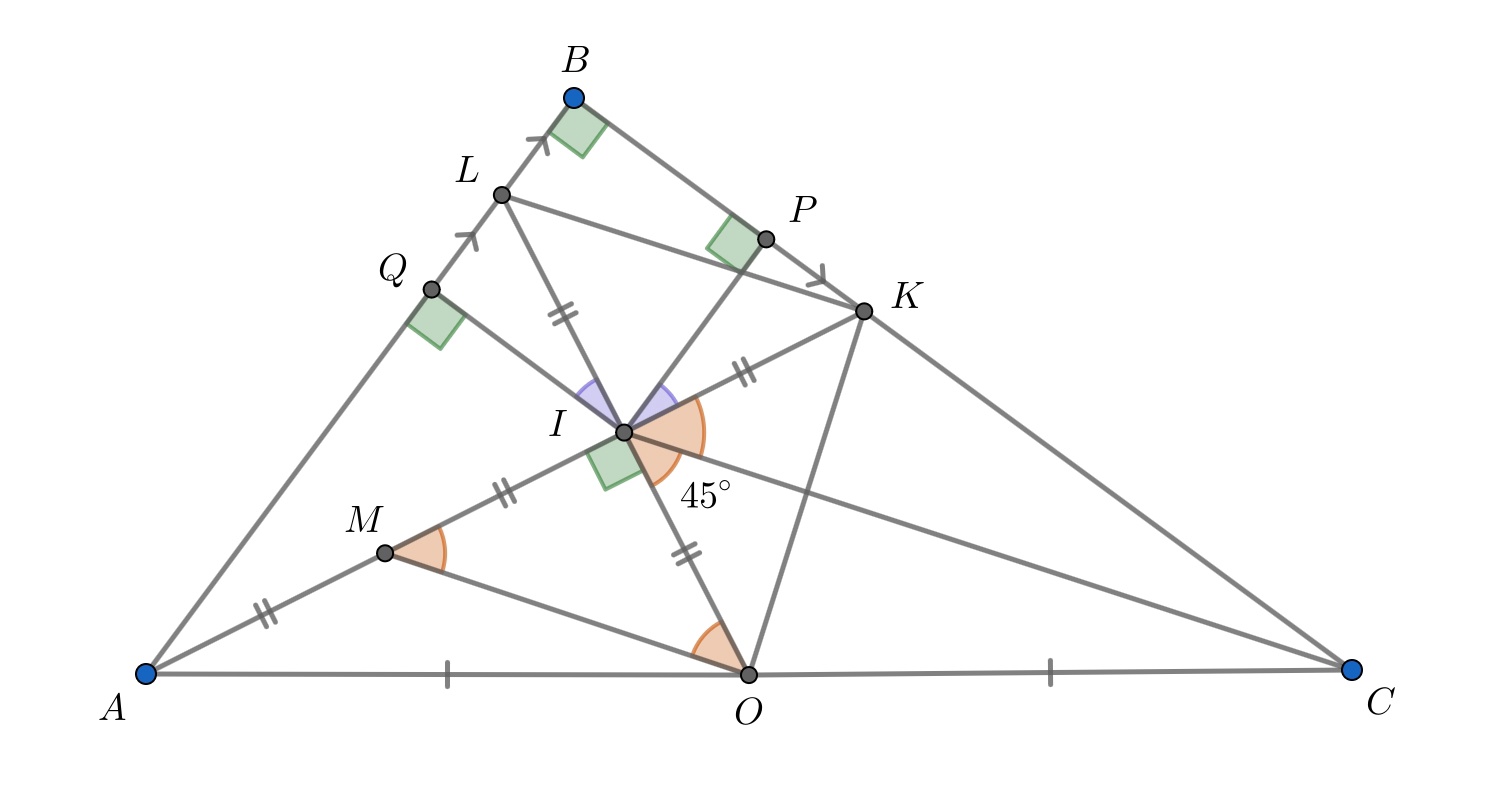
Опустим из точки перпендикуляры и на стороны и соответственно, точки и являются точками касания этих сторон со вписанной окружностью, четырёхугольник является квадратом. Углы и прямые, значит, углы и равны, отсюда следует равенство прямоугольных треугольников и По теореме Фалеса длина равна половине длины а длина вдвое больше длины

Следовательно, длина стороны равна Из теоремы Пифагора Следовательно,

______________________________________________________________________________________________________________________________________________________

Второе решение.

Пункт 1, точки те же, что как в первом решении, четырёхугольник является квадратом.

В прямоугольном треугольнике катет вдвое больше катета Считаем длину равной единице, тогда площадь треугольника равна длина гипотенузы АО равна , а высота из вершины равна . Эта высота и отрезки и равны, как радиусы вписанной окружности, поэтому

Следовательно,

Из теоремы Пифагора , откуда

Для каждой кучки назовём её показателем максимальную степень двойки, на которую делится число содержащихся в ней камней, она может быть равна . Рассмотрим поведение показателей кучек, участвующих в перекладывании. После перекладывания камней из кучки с камнями в кучку с камнями в первой остаётся камней, а во второй становится камней. Если , то

поэтому оба показателя возрастут. Если , то

где . При этом минимальный в данной паре кучек показатель сохраняется, а второй гарантированно становится больше минимального. Заметим, что количество кучек с минимальным среди всех показателем при произвольном перекладывании либо уменьшается на 2, либо не меняется.

Рассмотрим произвольную раскладку камней по более, чем одной кучке. В ней число кучек с минимальным показателем будет чётным. Действительно, общее число камней и сумма количеств камней в не минимальных кучках делятся на поэтому сумма количеств камней в минимальных кучках тоже делится на , значит, их количество делится на 2. Если в раскладке есть хотя бы две кучки, разбиваем все кучки с минимальным показателем на пары, выполняем в каждой перекладывание из большей в меньшую и получаем раскладку с большим минимальным показателем, чем рассматриваемая. Проделав эту процедуру не более, чем раз, получим раскладку с минимальным показателем , то есть с единственной кучкой из камней.

Пусть теперь не является степенью двойки. Рассмотрим любой процесс сборки некоторой раскладки N камней по кучкам в одну и произведём его в обратном порядке, посредством процедур перекладывания, обратных к исходным, когда половина одной из кучек перекладывается в другую. При этом в обратном процессе количество камней в первой кучке (она же последняя в исходном процессе сборки) и всех получающихся на каждом шаге будет делиться на нечётное число . Следовательно, любая раскладка, в которой есть кучка из числа камней, не делящегося на , не может быть собрана в одной кучке. В частности, не может быть собрана в одну раскладка по двум кучкам.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание. В случае можно предложить другое решение того, что раскладка по двум кучкам не может быть собрана в одну. Этого достаточно для доказательства необходимости в условии задачи, то есть того, что любая начальная раскладка N камней по кучкам может быть собрана в одной куче только тогда, когда N является степенью двойки.

Докажем по индукции, что после перекладываний количества камней в кучках имеют вид

для некоторого целого числа .

База индукции при очевидна:

то есть .

Шаг индукции: либо мы перекладываем камни из правой кучки в левую, тогда в левой станет , а в правой останется камней, при этом , либо мы перекладываем камни из левой кучки в правую, тогда в левой останется , а в правой станет камней, при этом .

Если после некоторого -ого перекладывания раскладки останется всего одна кучка, то число камней в другой станет равным 0 , следовательно, выполнится равенство одно из равенств или . В обоих случаях N будет делителем числа , то есть тоже степенью двойки противоречие с тем, что в рассматриваемом случае . Следовательно, при любом N , отличном от степени двойки, раскладка не может быть собрана в одну кучку.

_________________________________________________________________________________________________________________________________________________________________________________

Замечание. Объединяя оба случая и , получаем доказательство более общего утверждения: раскладка N камней может быть собрана в одной кучке тогда и только тогда, когда количество камней в каждой её кучке делится на набольший нечётный делитель N .