Теорема косинусов, теорема Пифагора, использование теоремы о трёх перпендикулярах
Ошибка.
Попробуйте повторить позже
Дана четырехугольная пирамида с высотой
Сфера радиуса 3 касается всех граней пирамиды, причем основания
эта сфера касается в точке
основания высоты. Найдите периметр четырехугольника
если известно, что его площадь
равна 144.
Источники:
Подсказка 1
Выразим объем четырехугольной пирамиды двумя способами, отсюда найдем площадь полной поверхности.
Подсказка 2
Мы знаем площадь полной поверхности, из чего она состоит? Как можно посчитать площадь треугольников?
Подсказка 3
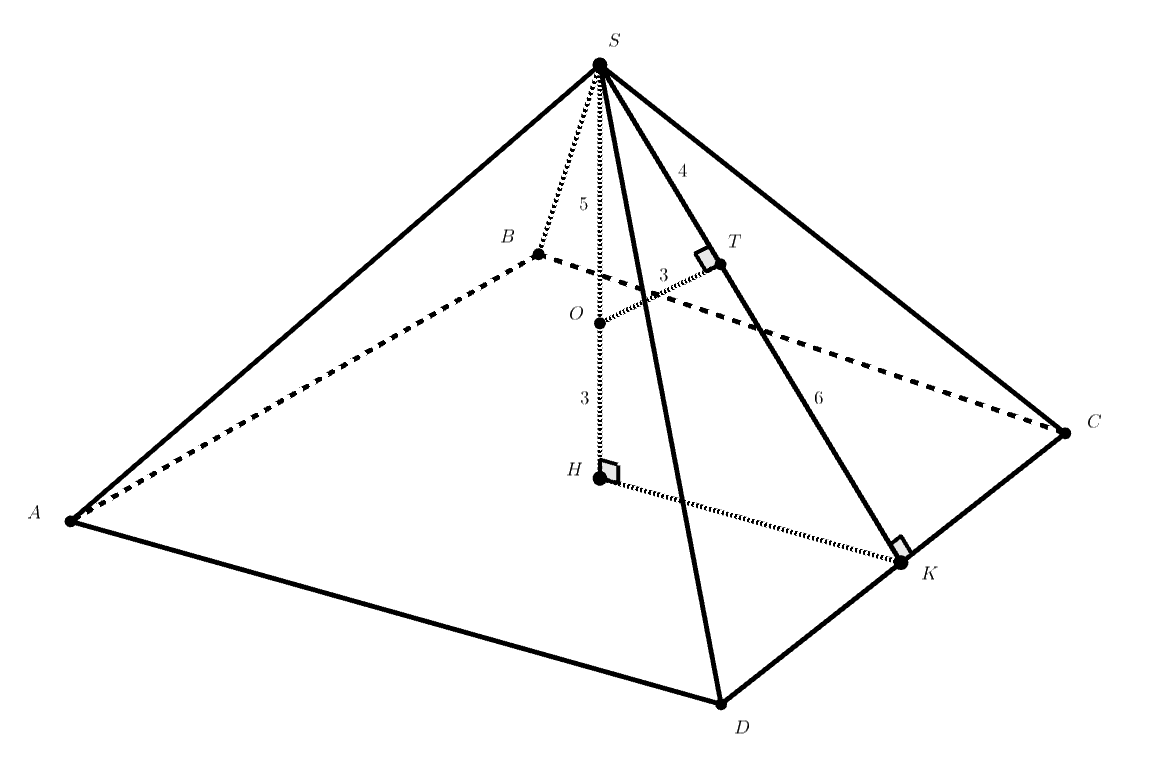
Попробуем дойти до высоты треугольника CSD. Проведем перпендикуляр OT из центра вписанной сферы к грани CSD, K — точка пересечения ST и CD. Можем ли мы теперь узнать высоту CSD?
Подсказка 4
Можем! Выражаем отрезки, пользуясь подобием треугольников, применяем теорему о трех перпендикулярах и получаем, что SK перпендикулярно CD. Что будет, если выполнить аналогичные действия для других граней?
Подсказка 5
Высоты в гранях равны. Используем площадь полной поверхности и выражаем периметр четырехугольника.
С одной стороны,
С другой, если — радиус вписанной сферы,
— площадь полной поверхности, то
Тогда
Пусть — центр вписанной сферы,
— перпендикуляр к грани
прямая
пересекает
в точке
Так как
то
а также
следовательно, в треугольнике
Кроме того,
подобен
следовательно,
По теореме о трех перпендикулярах, Заметим, что если мы будем опускать высоты на остальные грани
из точки
каждый раз будем получать те же самые подобные треугольники, следовательно, высоты в гранях равны.
Тогда
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




