Тема ДВИ в МГУ - задания по годам

ДВИ 2021

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела дви в мгу - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#32517

Найдите все значения параметра $a$ , при которых неравенство

6 6 2 sin x+ cos x+ a⋅sin2x≥ a

выполняется для всех действительных $x$ .

Источники: ДВИ - 2021, вариант 213, задача 6 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Сначала хочется избавиться от шестых степеней, причём 6 - чётное число. Можно ли как-то получить сумму 2k-ых степеней синуса и косинуса? Довольно классическим способом является возведение основного тригонометрического тождества в степень k, тогда получим нужную сумму, а также некоторое количество слагаемых, которые нужно вычесть из обеих частей полученного равенства. В данном случае возведём ОТТ в куб и выразим сумму шестых степеней.

Подсказка 2

После преобразований останется 1 - 3/4 sin²(2x). Тогда можно сделать замену t = sin(2x), получив квадратичную функцию от t, причём для определённости перепишем так, чтобы старший коэффициент был положительным. Как теперь можно переформулировать задачу? Если неравенство должно выполняться для любых иксов, то должно выполняться для всех t от -1 до 1. Тогда главный вопрос: в каком случае у параболы с ветвями вверх на всём некотором отрезке принимаются неположительные значения?

Подсказка 3

На самом деле, это верно в том и только том случае, если этот отрезок лежит между корнями (может быть, концы совпадают с корнями). А как записать условие на то, что отрезок лежит между корнями? Это значит, что на концах отрезка принимаются неположительные значения. Запишем систему из двух неравенств, и найдём подходящие значения a!

Показать ответ и решение

По формуле суммы кубов

6 6 2 2 4 2 2 4 sin x+ cos x =(sin x+ cos x)(sin x − sin xcos x+cos x)=

2 2 2 2 2 3 2 = (sin x +cosx) − 3sin xcosx =1 −4 sin 2x,

После замены $t= sin2x ∈[−1,1]$ можно переписать неравенство в виде

3 2 2 2 2 1 −4t + at≥a ⇐ ⇒ 3t− 4at+4(a − 1)≤ 0

Перед нами парабола, ветви которой направлены вверх, тогда выполнение неравенства для любого $t∈ [−1,1]$ эквивалентно тому, что корни лежат по разные стороны от этого отрезка (в том числе, быть может, на концах отрезка). А значит, тому, что неравенство выполнено в точках $±1$ :

{ 3− 4a +4a2− 4≤0 3+ 4a +4a2− 4≤0

{ 3− 4a +4a2− 4≤0 3+ 4a +4a2− 4≤0

( [1−√2 1+√2] { a ∈[--2√,-2--√-] ( a ∈ −1−2-2,−1+2-2

Пересекая отрезки, получаем ответ.

Ответ:

$[1− √2 −1+ √2] --2--;---2---$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#63561

Решите уравнение

4sin2xcos3x− 2sin5x= tg2x

Источники: ДВИ - 2021, вариант 215, задача 3 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Раскрывать по формуле синуса суммы и косинуса суммы тройные, а уж тем более “5-рные” углы мы не хотим. А что еще можно сделать с первым слагаемым левой части?

Подсказка 2

Конечно применить формулу произведения синусов! Тогда после преобразований получим выражение только с двойными углами. А с ними уже проще работать! Но не спешите применять формулу к тангенсу, ведь слева останется еще синус, который все портит. Попробуйте сначала перейти к выражению с синусами и косинусами!

Подсказка 3

Чтобы не работать с дробями – домножаем обе части на знаменатель (не забывая выписать ограничение) и теперь уже смело можем раскрывать двойные углы. Что общего у всех слагаемых?

Подсказка 4

Есть общий множитель! Выносим его за скобку, предварительно перенеся все в одну сторону – приговор для него уже подписан. А со скобкой, возможно, еще стоит поработать! Приведите ее к выражению, в котором есть только косинусы и числа. На что похоже полученное выражение?

Подсказка 5

Конечно на квадратный трехчлен! Вот только оно относительно функции, а не просто переменной. Ищем нули известным Вам способом и получаем уже простейшие тригонометрические уравнения! Для удобства можно ввести новую переменную t = cos (x) и решать квадратное относительно t уравнение.

Показать ответ и решение

Снова вспомним формулы $2sin2xcos3x= sin5x − sinx$ , тогда получим:

2(sin5x− sinx)− 2sin5x= tg2x

Домножим на $cos2x⁄= 0$ :

− 2sinxcos2x = sin2x= 2sinxcosx

Если $sinx =0$ , то $x =πn,n ∈ℤ$ , иначе

cosx+ cos2x= 0

2cos2x+ cosx− 1= 0

cosx= −1±-3 4

Тут можно заметить, что для $cosx= −1$ верно $sinx= 0$ , поэтому достаточно добавить в ответ серию для второго решения $x =± π3 + 2πn,n ∈ℤ$ . Очевидно, все корни подходят под условие $cos2x⁄= 0$ .

Ответ:

$πn,±π + 2πn, n∈ ℤ 3$

Ошибка.
Попробуйте повторить позже

Задача 3#63562

Решите уравнение

2 ctgx− 2ctg 2x = 3cosx

Источники: ДВИ - 2021, вариант 216, задача 3 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Не забываем выписать ОДЗ и смотрим на косинус справа. Он явно не даст нам работать только с тангенсами и котангенсами, значит, приводим все к выражению с косинусами и синусами!

Подсказка 2

Все еще остались двойные углы – самое время от них избавиться! А заодно и дроби собрать в одну, приведя к общему знаменателю. Приводите числитель к красивому итогу и смотрите, что получилось :)

Подсказка 3

А получилось уже совсем несложное тригонометрическое уравнение! Можем ли еще сильнее упростить его, перейдя к одной тригонометрической функции?

Подсказка 4

Если домножить обе части на знаменатель, то получится заменить квадрат косинуса на выражение с квадратом синуса по ОТТ! Остается лишь решить квадратичное уравнение и добить до ответа. Для удобства можно ввести новую переменную t = sin (x) и решать квадратное относительно t уравнение.

Показать ответ и решение

Учтём, что $sin 2x ⁄=0$ — это задаёт всю ОДЗ, далее преобразуем выражение слева:

cosx 2cos2x-− 1 1− cos2x sin-x ctgx− 2ctg2x= sin x − sinxcosx = sinxcosx = cosx

В итоге

2 sinx −3 ±5 1 3cosx = cosx-⇐⇒ 2sin2x +3sinx − 2 =0 =⇒ sinx=--4-- =− 2,2

То есть $sinx = 12,x= (−1)nπ6 + πn,n ∈ℤ$ (что удовлетворяет ОДЗ).

Ответ:

$(−1)nπ+ πn,n∈ ℤ 6$

Ошибка.
Попробуйте повторить позже

Задача 4#63815

Дан тетраэдр $ABCD$ . Известно, что центр сферы, описанной около этого тетраэдра, лежит на $AB$ , что плоскости $ABC$ и $ABD$ перпендикулярны и что $AD =DC = CB$ . Найдите угол между прямыми $AD$ и $CB.$

Источники: ДВИ - 2021, вариант 214, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Пусть К — центр описанной сферы. Отметьте равные отрезки-радиусы сферы. Какой вывод можно сделать, смотря на △ADB и его медиану, равную половине стороны? Какой вывод можно сделать о △АВС?

Подсказка 2

Итак, перед нами два прямоугольных треугольника с общей гипотенузой и равными катетами, значит они сами...? Проведите высоту DH в △ADB, что можно сказать об отрезке СН, пользуясь перпендикулярностью плоскостей?

Подсказка 3

Из равенства треугольников можно вывести, что ВН = АН, то есть Н совпадает с К, значит △ADB и △AСB не только прямоугольные, но и...?

Подсказка 4

Отметьте L и M — середины рёбер BD и CD соответственно. Что можно сказать о связи LM и BC? А о LK и AD? Осталось внимательно рассмотреть △MLK и записать ответ!

Показать ответ и решение

Сразу отметим, что, поскольку центр сферы, описанной около тетраэдра, лежит на $AB$ , углы $ACB$ и $ADB$ - прямые.

$PIC$

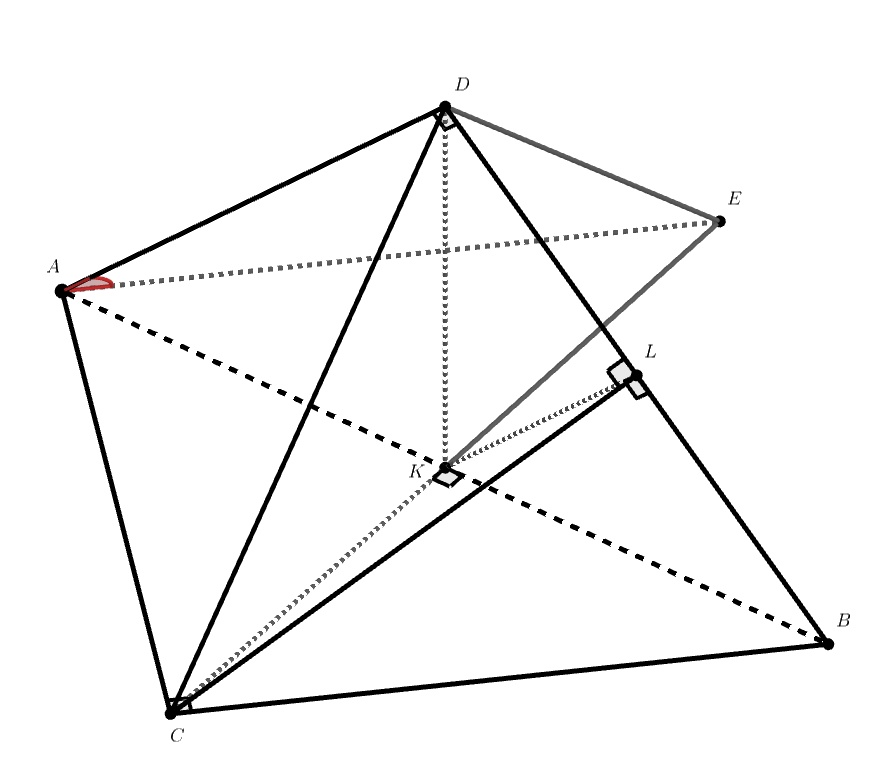
Далее, опустим перпендикуляры $CK$ и $CL$ на $AB$ и $BD$ соответственно. Тогда $DL = LB$ , ибо $DC = CB$ , следовательно, $KL −$ серединный перпендикуляр к $BD$ в плоскости $ABD$ и, поскольку $∘ ∠ADB = 90$ , точка $K$ является серединой $AB$ . Значит, $AC =BC$ . Аналогично, $AD = BD.$

Итак, $AC = BC = AD =BD =CD, AB ⊥CK, AB ⊥DK, AK = BK = CK =DK$ . Пусть $E −$ точка, симметричная точке $C$ относительно $K$ . Тогда $AK ⊥ EK ⊥ DK$ и $AK = EK =DK$ . Следовательно, треугольник $ADE −$ равносторонний. При этом $AE ∥CB$ . Стало быть, искомый угол равен углу $EAD$ и равен $60∘.$

Ответ:

$60∘$

Ошибка.
Попробуйте повторить позже

Задача 5#63816

Дан параллелепипед $ABCDA ′B′C′D′$ с основаниями $ABCD, A ′B′C′D′$ и боковыми рёбрами $AA ′,BB′,CC′,DD ′.$ Все рёбра параллелепипеда равны. Плоские углы при вершине $B$ также равны. Известно, что центр сферы, описанной около тетраэдра $′ ′ AB CD ,$ лежит в плоскости $′ AB C.$ Радиус этой сферы равен $2.$ Найдите длину ребра параллелепипеда.

Источники: ДВИ - 2021, вариант 216, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

В вершине В сходятся 3 равных угла, что можно сказать об отрезках-диагоналях граней, лежащих напротив этой вершины? (Строго обосновать этот факт можно через треугольники, равные по 2-м сторонам и углу между ними!)

Подсказка 2

В какой ещё из вершин параллелепипеда сходятся 3 равных угла? Какой вывод можно сделать об отрезках-диагоналях граней, исходящих из этой же вершины?

Подсказка 3

Каким свойством в таком случае обладает тетраэдр D'AB'C: у него равны боковые рёбра и в основании лежит правильный треугольник? Таким образом мы можем вычислить все его стороны!

Подсказка 4

Восстановите длину стороны ромбов-граней по найденным диагоналям и можно записывать ответ!

Показать ответ и решение

$PIC$

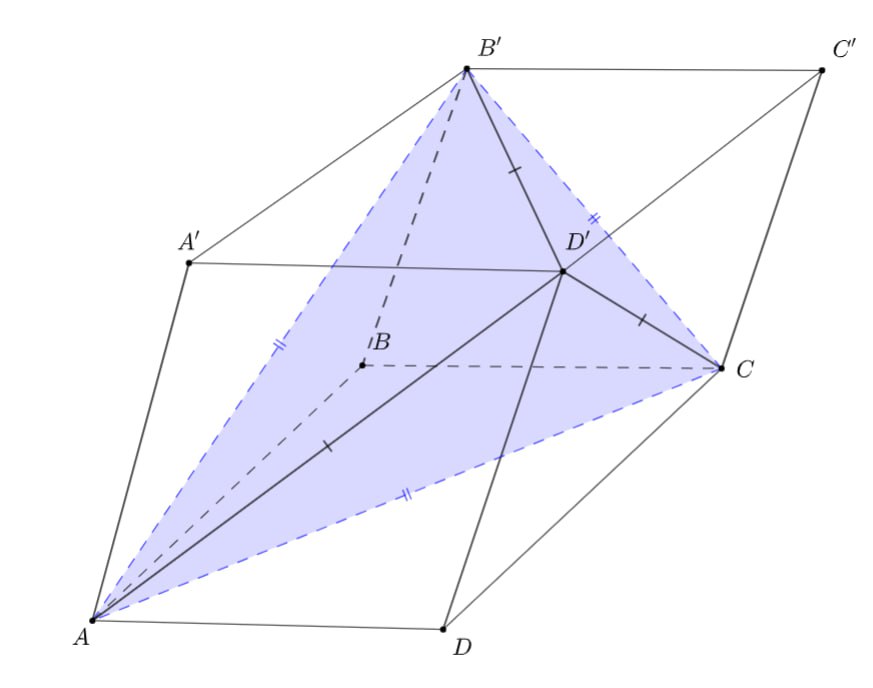
Грани параллелепипеда являются ромбами. Поскольку плоские углы при вершине $B$ равны, равны также и плоские углы при вершине $D ′$ . Стало быть, $AD′ = B′D′ = CD ′$ как равные диагонали ромбов и, по той же причине, $AB ′ = B′C = AC$ . Таким образом, центр сферы, описанной около тетраэдра $AB′CD′$ , является центром окружности, описанной около правильного треугольника $AB′C$ , а также является основанием высоты тетраэдра, опущенной из вершины $D′$ . Отсюда получаем $√ - √ - AB ′ =2 3,AD ′ =2 2$ . Итак, диагонали ромба равны $- 2√ 3$ и $- 2√ 2$ , значит, его сторона равна $- √ 5.$

Ответ:

$√5$

Ошибка.
Попробуйте повторить позже

Задача 6#63818

Вписанная в треугольную пирамиду $ABCD$ сфера касается граней $BCD, ACD,ABD$ и $ABC$ в точках $A ,B ,C 1 1 1$ и $D 1$ соответственно. Известно, что $D1$ является точкой пересечения высот треугольника $ABC$ , что плоскости $ABC$ и $A1B1C1$ параллельны и что радиус окружности, описанной около треугольника $ABC$ в четыре раза больше радиуса окружности, описанной около треугольника $A1B1C1$ . Найдите отношение, в котором сфера делит отрезок $DD1$ , считая от вершины $D.$

Источники: ДВИ - 2021, вариант 213, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

В задаче фигурирует ортоцентр, это явно неспроста. Пусть А2, B2, C2 - вершины ортотреугольника и О - центр сферы. Что можно заметить?

Подсказка 2

Представляют интерес четырехугольники OA1A2D1, OB1B2D1, OC1C2D1. На какие фигуры их можно разбить?

Подсказка 3

Они разбиваются на равные прямоугольные треугольники! Можем поотмечать равные углы и затем отметить равные отрезки.

Подсказка 4

В итоге имеем, что D1 - точка пересечения биссектрис АВС. Что тогда можем сказать?

Подсказка 5

ABC - правильный треугольник! (так как его ортоцентр совпал с инцентром) Тогда мы можем сказать какая прямая является высотой пирамиды.

Подсказка 6

Остается провести радиусы окружностей из условия и в вспомогательной плоскости поработать с нашей конструкцией.

Показать ответ и решение

Пусть $O$ — центр сферы и пусть $A ,B ,C 2 2 2$ — основания высот треугольника $ABC$ , опущенных из вершин $A,B,C$ соответственно.

$PIC$

Рассмотрим четырёхугольники $OA1A2D1$ , $OB1B2D1,OC1C2D1$ . Каждый из них состоит из двух равных прямоугольных треугольников. При этом катеты $OD1,OA1,OB1, OC1$ равны.

Из равенства расстояний от $A1,B1,C1$ до плоскости $ABC$ следует, что равны углы $D1OA1,D1OB1,D1OC1$ , а стало быть, равны и углы $D1A2A1$ , $D1B2B1,D1C2C1$ . Значит, равны отрезки $D1A2,D1B2,D1C2$ , то есть $D1$ является точкой пересечения биссектрис треугольника $ABC$ . При этом $D1$ это ортоцентр $ABC$ . Стало быть, треугольник $ABC$ правильный. Поскольку углы $D1A2A1,D1B2B1,D1C2C1$ равны, $DD1$ — высота пирамиды. Опустим из $A1$ перпендикуляр $A1D2$ на $DD1$ . Тогда радиус окружности, описанной около треугольника $A1B1C1$ равен $A1D2$ . Радиус же окружности, описанной около треугольника $ABC$ равен $AD1$ . Получаем, что $A2D1 = 1AD1 = 1 ⋅4A1D2 = 2A1D2 2 2$ . Отсюда видим, что $∠D1A2A1 = 60∘$ . Стало быть, $DD1 = √3⋅A2D1 = √3⋅√3⋅OD1 = 3OD1$ . Получаем, что искомое отношение равно $(DD1 − 2OD1 ):2OD1 = 1:2.$

Ответ:

$1 :2$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#63819

Сфера касается всех рёбер тетраэдра $ABCD$ . Известно, что произведения длин скрещивающихся рёбер равны. Известно также, что $AB = 3,BC = 1$ . Найдите $AC.$

Источники: ДВИ - 2021, вариант 215, задача 7 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Подумаем, как можно применить условие о том, что сфера касается всех рёбер тетраэдра? Более всего с длинами рёбер тут связывается свойство касательных: отрезки касательных к сфере, проведенных из одной точки, равны! Обозначьте одной буквой все равные отрезки проведённые из каждой из вершин и при помощи этих букв запишите равенство произведений длин скрещивающихся рёбер. ---

Подсказка 2

Поработайте теперь с нашим двойным равенством: рассмотрите две пары уравнений и попробуйте их преобразовать. Какие интересности связанные с отрезками касательных из разных вершин можно заметить?

Подсказка 3

Если сделать всё аккуратно, то получится несколько вариантов: равны либо отрезки касательных проведённые из вершин А и С, либо проведённые из вершин В и D. Рассмотрите оба случая, не выходит ли в одном из них противоречий с условием задачи? (Не зря же нам даны AB и BC). Аналогично рассмотрите вторую пару вершин, отрезки касательных из которых равны. Останется лишь внимательная арифметика и АС откроется нам!

Показать ответ и решение

Расстояния от вершины $A$ до точек касания сферы с рёбрами $AB,AC,AD$ равны. Обозначим это расстояние $a$ . Соответствующие расстояния от вершин $B,C,D$ обозначим $b,c$ , $d$ соответственно.

$PIC$

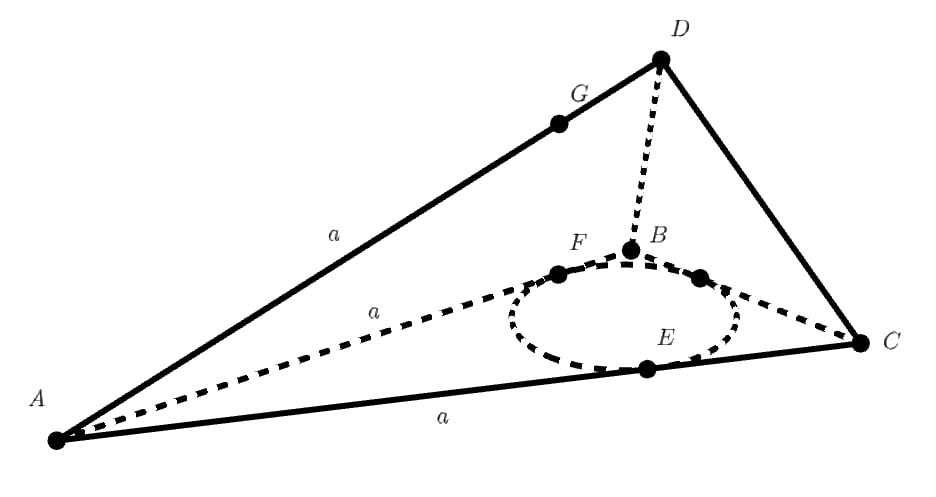
По условию $(a+b)(c+ d)= (a+ c)(b+ d)=(a+ d)(b+ c)$ , что равносильно после раскрытия скобок системе

(a− c)(b− d)= 0 и (a − b)(c− d)= 0.

Если $a= c$ , то $AB =BC$ , а это не так. Значит, $b= d$ . Тогда либо $a= b$ , либо $c =b$ . Если $a =b$ , то $AC = BC = 1$ , что противоречит неравенству треугольника. Значит, $c=b$ и, стало быть, $AC =AB = 3.$

Замечание.

Тетраэдр, у которого произведения длин скрещивающихся рёбер равны, называется каркасным, можете поизучать его свойства. В задаче по сути просили доказать, что у такого тетраэдра суммы длин скрещивающихся рёбер равны.

Ответ:

$3$

Ошибка.
Попробуйте повторить позже

Задача 8#63857

Решите неравенство

( logx log 2 ) logx−1 4 3 − 6x 3 + 10 ≤0

Источники: ДВИ - 2021, вариант 215, задача 4 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

В самом начале запишите ОДЗ. А теперь давайте поработаем с аргументом логарифма. Преобразуйте степени так, чтобы у нас в показателях степеней везде были одинаковые логарифмы от чисел, а чтобы переменная х была только в основаниях степеней!

Подсказка 2

Посмотрите внимательно на то, какой формулой сокращенного умножения мы можем воспользоваться в аргументе логарифма, чтобы нам стало чуть-чуть удобнее с ним работать! Да, мы не можем разложить все на множители, но тем не менее есть способы упростить себе жизнь!

Подсказка 3

Верно, мы можем выделить полный квадрат! Дальше просто действуем по методу рационализации, вспоминаем про то, что квадрат не может принимать отрицательные значения и добиваем задачу!

Показать ответ и решение

В силу тождества $xlog32 = 2log3x$ неравенство эквивалентно

(( log x )2 ) logx−1 2 3 − 3 +1 ≤0

Тогда на ОДЗ:

{ x− 1> 0 x− 1⁄= 1

неравенство по методу рационализации сводится к

( )2 (x− 2) 2log3x− 3 ≤ 0

откуда либо

2log3x− 3= 0 ⇐⇒ log3x= log23 ⇐⇒ x= 3log23,

либо

x≤ 2

Пересекаем с ОДЗ и получаем ответ.

Ответ:

$(1;2)∪ {3log23}$

Ошибка.
Попробуйте повторить позже

Задача 9#63901

Автовладелец Авдей продал автосалону свой автомобиль за $60%$ его первоначальной стоимости. Автосалон выставил на продажу этот автомобиль за цену, на $20%$ большую уплаченной Авдею. Какова доля получившейся цены по отношению к первоначальной?

Источники: ДВИ - 2021, вариант 213, задача 2 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте обозначим первоначальную стоимость автомобиля за х. Попробуйте теперь выразить все остальные стоимости автомобиля!

Подсказка 2

Для этого будем действовать последовательно. Выразите стоимость, за которую Авдей продал его обратно в автосалон. А за какую стоимость автосалон выставил автомобиль на продажу?

Подсказка 3

Дело за малым, осталось только вспомнить, о чем нас спрашивают в задаче и посчитать нужное число!

Показать ответ и решение

Пусть автомобиль стоил $x$ (у.е.), тогда Авдей продал его за $0.6x$ , а затем его выставили на продажу за $1.2⋅0.6x= 0.72x$ , так что доля равна $72%.$

Ответ:

$72%$

Ошибка.
Попробуйте повторить позже

Задача 10#64114

Найдите все пары действительных чисел $(x,y)$ с наименьшим возможным значением $y$ , удовлетворяющие неравенству

( 2 7) logx2−y x− y + 4 ≥ 1

Источники: ДВИ - 2021, вариант 215, задача 6 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

От чего зависит сохранение или изменение знака неравенства в работе с логарифмами? Рассмотрите соответствующие два случая в зависимости от основания log.

Подсказка 2

Попробуйте графически изобразить неравенство равносильное нашему для случая, когда основание логарифма больше 1. Для этого выделите полные квадраты. Значение у должно быть наименьшим, значит нас интересует самая нижняя точка графика. Удовлетворяет ли она условию, заданному основанием логарифма?

Подсказка 3

Рассмотрите второй случай: основание log меньше 1. Обратите внимание, могут ли при этом получиться у меньшие или равные найденного ранее минимума? Запишите итоговый ответ.

Показать ответ и решение

При $y < x2− 1$ неравенство равносильно $x− y2+ 7≥ x2− y 4$ , то есть

1 2 1 2 3 2 (x −2) + (y −2 )≤ (2)

Это неравенство задаёт круг с центром $1 1 (2; 2)$ и радиусом $3 2.$ Самая нижняя точка имеет координаты $1 (2; −1)$ и удовлетворяет ограничению $2 y <x − 1$ .

$PIC$

При $y > x2− 1$ для каждой пары $(x,y)$ , удовлетворяющей исходному неравенству, справедливо $y > −1$ . Стало быть, искомое множество состоит ровно из одной точки $(1; −1). 2$

Ответ:

$(1;−1) 2$

Ошибка.
Попробуйте повторить позже

Задача 11#90014

Решите уравнение

sin3x−-sinx- √- ( 2 ) 2⋅cos3x+ cosx = 3⋅ 1− tg x .

Источники: ДВИ - 2021, вариант 213, задача 3 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Подумаем, а как можно преобразовать числитель и знаменатель? Какие формулы можно применить?

Подсказка 2

Распишем числитель и знаменатель по формулам преобразования суммы триг. функций в произведение. Чему тогда равна левая часть после преобразований?

Подсказка 3

Получаем, что 2*tg(x) = √3 * (1 - tg²(x)). Несложно заметить, что это квадратное уравнение относительно tg(x). Решаем его и не забываем про ОДЗ ;)

Показать ответ и решение

Преобразуем разность синусов и сумму косинусов в произведения:

2cos2xsinx √ - 2 2⋅2cos2x cosx = 3(1− tgx)

Запишем ОДЗ:

( π πk ||{ x⁄= 4 +-2 cos3x+ cosx ⁄=0;cosx ⁄=0 ⇐ ⇒ || π ( x⁄= 2 +πk, k ∈ℤ

Тогда получаем следующее:

√- √ - √- 2tgx= 3(1 − tg2x) ⇐ ⇒ 3tg2x +2tgx− 3 =0

⌊ √- ⌊ 2π tgx= −√-3 | x= 3-+ πk ⌈ tgx= -3- ⇐⇒ |⌈ π 3 x= 6 + πk,

Объединяя решения и пересекая их с ОДЗ, получаем:

x = π+ πk, k∈ℤ 6 2

Ответ:

$π + πk, k∈ ℤ 6 2$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#91775

Бобер доплывает от своей норы вниз по реке до осиновой рощи за три минуты. Подкрепившись, он плывет обратно к своей норе, на что у него уходит четыре минуты. Во сколько раз собственная скорость бобра превышает скорость течения? (Собственную скорость бобра считать постоянной).

Источники: ДВИ - 2021, вариант 214, задача 2 (pk.math.msu.ru)

Показать ответ и решение

Пусть $x$ — скорость бобра в неподвижной воде, $y$ — скорость течения реки (в м/мин). Заполним таблицу, отражающую связь между величинами, описывающими движение:


	$v$ , м/мин	$t$ , мин	$s$ , м

По течению	$x+ y$	3	$3(x +y)$

Против течения	$x− y$	4	$4(x − y)$

Поскольку бобёр проплывает одинаковые расстояния по течению реки и против течения то,

4(x− y)= 3(x+ y); 4x− 4y = 3x+ 3y; x = 7y.

Таким образом, собственная скорость бобра в 7 раз больше скорости течения реки.

Ответ: в 7 раз

Ошибка.
Попробуйте повторить позже

Задача 13#92350

Найдите все значения параметра $a$ , при которых уравнение

(∘ -------2- ∘--------2)(∘----2 ∘ -------2)(∘ ---2- ∘ -------2) 3+2x − x − 3 − 2x− x a − x − 3− 2x− x a− x − 3+ 2x − x = 0

имеет ровно одно решение.

Источники: ДВИ - 2021, вариант 214, задача 6 (pk.math.msu.ru)

Подсказки к задаче

Подсказка

В уравнении встречаются три разных корня, два из них без параметра, значит, их графики сразу можно начертить. А вот третий график будет изменяться при разных значениях а. Чтобы понять, какие значения параметра а подходят, не забудьте про ОДЗ!

Показать ответ и решение

Запишем ОДЗ:

(| 3− 2x− x2 ≥ 0 |||{ | 3+2x− x2 ≥ 0 |||( a− x2 ≥0

(|| (x +1)2 ≤ 4 ||{ || (x − 1)2 ≤ 4 ||( x2 ≤ a

Видно, что если $a< 0,$ то решений нет, поэтому пусть $a ≥0.$

( ||| x∈ [−3;1] |{ ||| x∈ [−1;3] |( x∈ [− √a;√a]

Получаем, что $x$ принадлежит пересечением отрезков $[−1;1]$ и $[ √ -√-] − a; a .$

Заметим, что

2 2 2 3±2x − x = 2 − (x∓ 1)

Стало быть, графики функций $√3-+2x−-x2$ и $√3−-2x−-x2-$ — верхние половины окружностей радиуса 2 с центрами в точках $(1,0)$ и $(−1,0)$ соответственно. График же функции $√a−-x2$ — верхняя половина окружности радиуса $√a$ с центром в точке $(0,0).$ Первые две полуокружности имеют одну общую точку — $(0,√3-).$

$PIC$

Рассмотрим несколько случаев: 1) При $a <1$ третья полуокружность первые две не пересекает и решение будет одно.

$PIC$

2) При $1≤ a≤ 5$ третья полуокружность пересекает первые две в точках с абсциссами из отрезка $[−1;1].$

$PIC$

3) При $a= 3$ точки пересечения совпадают.

$PIC$

4) При $a> 5$ третья полуокружность либо пересекает первые две в точках с абсциссами по модулю большими 1, либо не пересекает вообще.

$PIC$

Стало быть, решение будет единственным при $a∈ [0;1)∪ {3} ∪(5;+∞ ).$

Ответ:

$[0;1)∪{3}∪ (5;+∞ )$

Ошибка.
Попробуйте повторить позже

Задача 14#127156

Найдите произведение корней уравнения

x2+-x+-1 x2-− x+-1 x2-− 4x+-1 π−-2 sin 2x + cos 2x = x ⋅cos 4 .

Показать ответ и решение

Положим $t= x2+1-= 1(x+ 1) 2x 2 x$ . Тогда исходное уравнение примет вид

( 1) ( 1) π−-2 sin t+ 2 + cos t− 2 = 2(t− 2)cos 4 .

Заметим, что

sin(t+ 1∕2)+ cos(t− 1∕2)= sint(cos(1∕2)+ sin(1∕2))+cost(cos(1∕2)+ sin(1∕2)) = = (sin t+ cost)(cos(1∕2)+sin(1∕2))= 2cos(t− π∕4)cos(π∕4− 1∕2)

Получаем

cos(t− π∕4)= t− 2.

На отрезке [1,3] функция $cos(t− π∕4)$ убывает, ибо $3< π < 4$ . Функция же $t− 2$ на этом отрезке возрастает. Следовательно, графики этих функций имеют ровно одну общую точку при некотором $t= t0$ . Поскольку $t0 > 1$ , уравнение $x2− 2t0x+ 1= 0$ имеет два различных корня. Их произведение равно $1.$

Ответ: 1