Тема ДВИ в МГУ - задания по годам

ДВИ 2016

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела дви в мгу - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#64038

Решите неравенство

( 2 ) log1−log3x 1+logx 3 ≤1

Источники: ДВИ - 2016, задача 4 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Выписываем ОДЗ и сразу замечаем, что одно из условий выполнится автоматически! Тогда можем перенести все в одну сторону, чтобы сравнивать с нулем. Какой метод хорошо работает с логарифмами, когда с нулем сравниваем?

Подсказка 2

Конечно же метод рационализации! Представляем 1 как логарифм с нужным основанием и получаем уже более приятное неравенство. Для удобства можно ввести замену log₃(x) = t. Можем ли тогда и второй логарифм через эту переменную переписать?

Подсказка 3

С помощью подходящего свойства “переворачиваем” его и получаем рациональное неравенство, которое можем легко решить! Останется только произвести обратную замену.

Подсказка 4

Чтобы решить неравенства с обратной заменой достаточно воспользоваться монотонностью логарифма или применить снова метод рационализации!

Показать ответ и решение

ОДЗ:

( 1− log x >0 ||||| 1− log3x ⁄=1 |{ 3 ⇐⇒ x∈ (0,1)∪(1,3) ||| x ⁄=1 |||( x >20 logx 3+1 >0

Теперь применим метод рационализации. Исходное неравенство равносильно:

2 1+-log33x 1+-log3x (1− log3x− 1)(1+logx 3− 1 +log3x)≤ 0⇐ ⇒ log3x ≥ 0⇐ ⇒ log3x ≥ 0

Не забываем, что $logab =1∕logba$ и неполный квадрат при разложении суммы кубов строго положителен. Теперь нетрудно найти решения:

log3x∈ (−∞, −1]∪(0,+ ∞)=⇒ x ∈(0,1]∪ (1,3) 3

Пересекая с ОДЗ, получаем ответ.

Ответ:

$(0;1]∪(1;3) 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#64471

Две окружности касаются внутренним образом в точке $T$ . Хорда $AB$ внешней окружности касается внутренней окружности в точке $S$ . Прямая $TS$ пересекает внешнюю окружность в точках $T$ и $C$ . Найдите площадь четырёхугольника $T ACB$ , если известно, что $CB = BT = 3$ , а радиусы окружностей относятся как $5:8.$

Источники: ДВИ - 2016, задача 5 (pk.math.msu.ru)

Подсказки к задаче

Подсказка 1

Обозначим через Х и У точки пересечения внутренней окружности с отрезками АТ и ВТ. Вспомните про лемму Архимеда. Что можно сказать про отрезки АВ и ХУ?

Подсказка 2

Да, они параллельны! Вспомните о том, какие у нас есть вообще теоремы, в которых мы говорим об отношениях отрезков и которые похожи на эту задачу. В первую очередь, мы умеем работать с подобными треугольниками и во-вторых, у нас есть теорема о касательной и секущей! Воспользуйтесь ими, чтобы найти максимум отношений отрезков!

Подсказка 3

Посмотрите на отношения AS/BS и AT/BT. Какую теорему напоминает?

Подсказка 4

Верно, это обратная теорема о биссектрисе! Отметьте все равные углы, которые найдете и поищите параллельные прямые!

Подсказка 5

Посмотрите внимательно на четырехугольник ТАВС. Что можно о нем сказать? Воспользуйтесь всем, что узнали о четырехугольниках, о подобных треугольниках и попробуйте посчитать те величины, которые считаются!

Подсказка 6

Помните, если у нас есть трапеция, для вычисления ее площади мы можем найти высоту и среднюю линию и посчитать площадь, зная уже эти величины!

Показать ответ и решение

$PIC$

Обозначим через $X$ и $Y$ точки пересечения внутренней окружности с отрезками $AT$ и $BT$ соответственно.

Проведём общую касательную окружностей в точке $T.$ Тогда угол между касательной и хордой большей окружности $BT$ равен углу $BAT$ и тот же угол между касательной и хордой $TY$ меньшей окружности равен углу $YTX.$

∠BAT = ∠YXT, ∠BTA = ∠YTX =⇒

△BAT ∼ △Y XT =⇒ AT-= AX- BT BY

Применяя теорему о касательной и секущей, получаем

AS2-= AX-⋅AT-= AT2, BS2 BY ⋅BT BT2

то есть,

AS- AT- BS = BT,

что в силу обратной теоремы о биссектрисе означает, что $∠ATS = ∠BTS$ . Но из равенства $CB = BT$ следует, что

∠CT B =∠T CB,

стало быть, $AT∥CB$ , то есть четырёхугольник $TACB$ - трапеция, причём вписанная, то есть равнобокая. Значит, $AC = CB = BT =3$ .

Далее, треугольники $ATS$ и $BCS$ подобны с коэффициентом подобия $T S∕CS = = 5∕(8− 5)=$ 5/3. Следовательно, $AT = 5$ , а средняя линия трапеции $TACB$ равна 4. Высота же трапеции равна катету прямоугольного треугольника с гипотенузой 3 и другим катетом 1 , то есть равна $√ - 2 2$ . Таким образом, искомая площадь равна $√- √ - 4⋅2 2 =8 2$ .

Ответ:

$8√2$

Ошибка.
Попробуйте повторить позже

Задача 3#90318

Разность между наибольшим и наименьшим корнями уравнения $x2+ ax− 6= 0$ равна 5. Найдите все возможные значения $a$ .

Источники: ДВИ - 2016, вариант 1, задача 2 (pk.math.msu.ru)

Подсказки к задаче

Подсказка

Запишите в явном виде выражение для разности корней и найдите с помощью него дискриминант, теперь остается лишь найти значения а, при которых достигается данное значение дискриминанта

Показать ответ и решение

Из условия получаем

√-- |x1 − x2|=| D |=5 =⇒ D =25

Запишем дискриминант

2 2 2 D =a − 4⋅(−6)= a +24= 25 =⇒ a = 1

a= ±1

Ответ:

$a =±1$

Ошибка.
Попробуйте повторить позже

Задача 4#127819

Ровно в $9:00$ из пункта А в пункт Б выехал автомобиль. Проехав две третьих пути, наблюдательный водитель автомобиля заметил, что мимо него в сторону пункта А проехал некий велосипедист. В тот самый момент, когда автомобиль прибыл в пункт Б, из пункта Б в пункт А выехал автобус. Когда до пункта А оставалось две пятых пути, не менее наблюдательный водитель автобуса заметил, что он поравнялся с тем самым велосипедистом. Во сколько приедет велосипедист в пункт А, если известно, что автобус прибыл в пункт А ровно в $11:00?$ Скорости велосипедиста, автомобиля и автобуса считать постоянными.

Показать ответ и решение

Изобразим условие задачи в координатах по времени и положению в пространстве. Пусть точка $A′$ соответствует нахождению в пункте А в $9:00,$ автомобиль выехал из нее и прибыл в пункт Б, пусть это произошло в точке $B.$ Проехав $2 3$ пути, водитель заметил, что в сторону пункта А выехал велосипедист. Обозначим эту точку за $X.$ Пусть расстояние от A до Б равно $3x,$ тогда $′ A X =2x,$ $XB = x.$ В то же время, что автомобиль прибыл в пункт Б, из пункта Б выехал автобус в пункт А. Следовательно, момент выезда автобуса соответствует точке $B.$ Автобус прибыл в пункт А в $11:00,$ пусть это будет точка $C.$ Когда автобусу оставалось проехать $2 5$ пути, он поравнялся с велосипедистом, обозначим эту точку за $Y.$ Пусть расстояние от A до B равно $5y,$ тогда $BY = 3y,$ $YC =2y.$ Продлим прямую $XY$ до пересечения с осью $t$ в точке $Z.$

$PIC$

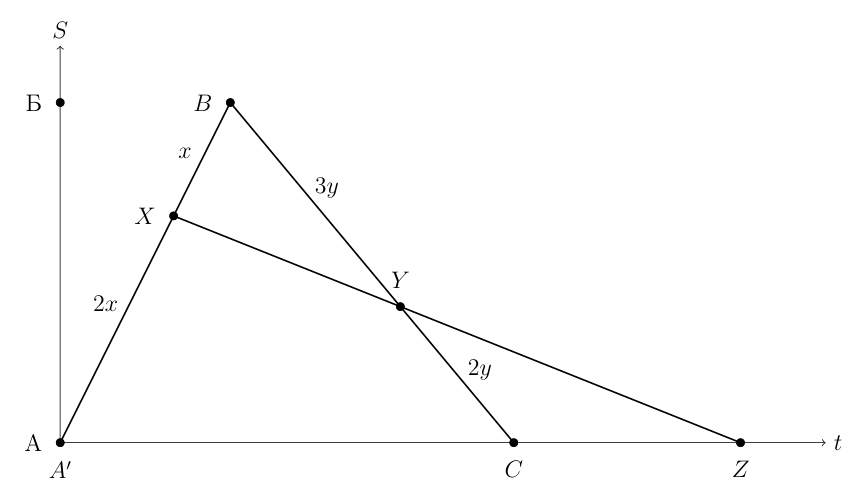
Точка $Z$ будет соответствовать прибытию велосипедиста в пункт A, так как он двигался с постоянной скоростью. Рассмотрим треугольник $A′BC$ и прямую $XZ.$ По теореме Менелая