№14 из ЕГЭ 2025
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Дан куб со стороной
На стороне
отмечена точка
такая, что
Через точки
и
проходит плоскость
параллельная
прямой
а) Докажите, что если
— точка пересечения
с прямой
б) Найдите меньший из отрезков, на которые плоскость делит диагональ
Источники:
а) Рассмотрим плоскость Пусть прямая
пересекает
в
точке
Так как плоскость
то
и прямая
обязательно
параллельна
По теореме о пропорциональных отрезках для параллельных
прямых
и угла
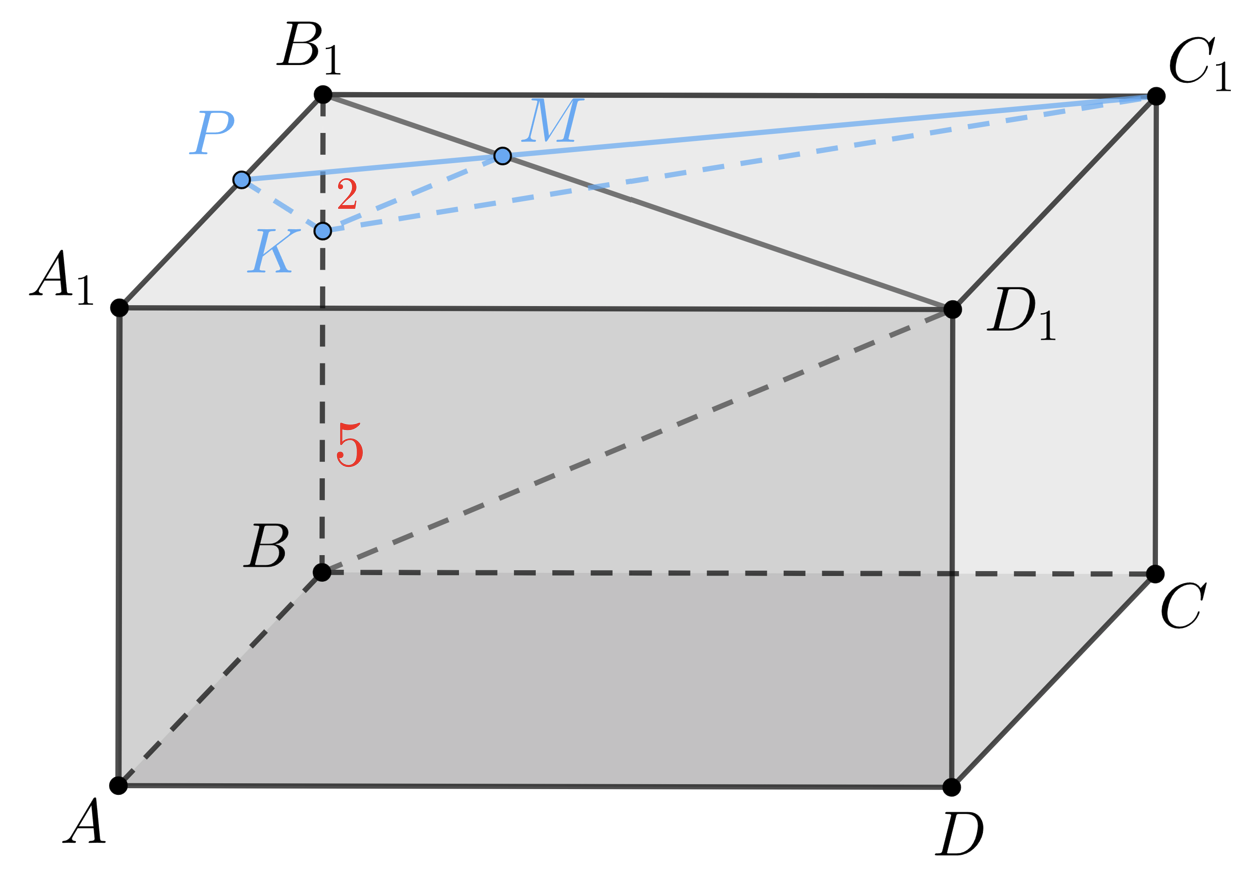
Рассмотрим плоскость Треугольники
и
подобны по двум углам, так как
как вертикальные и
как накрест лежащие при
Тогда
имеем:
Отсюда получаем, что
Тогда если то
и
Отсюда следует, что
б) Рассмотрим плоскость Тогда
как диагональ
квадрата со стороной
и
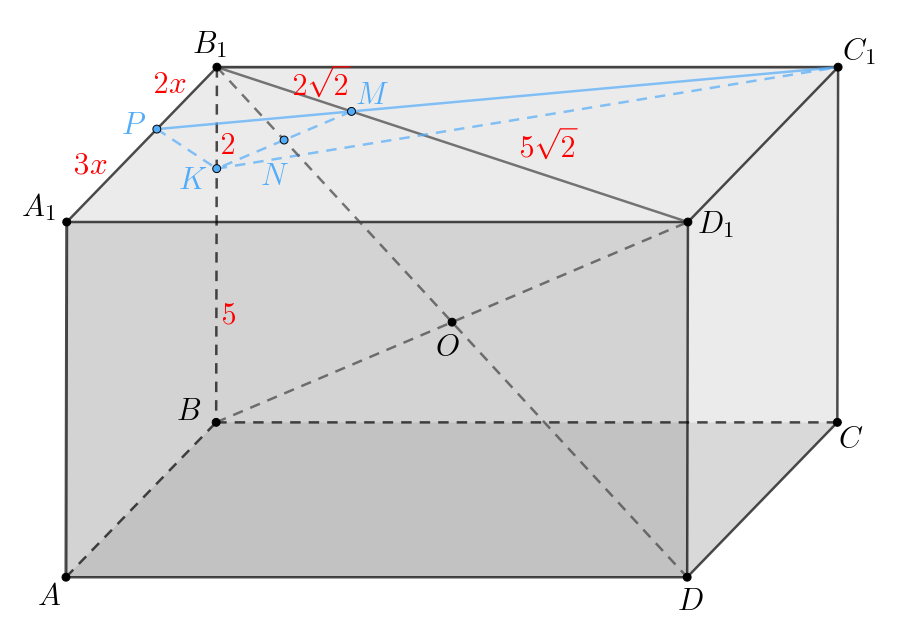
Рассмотрим плоскость Пусть
— точка пересечения диагоналей
куба и
Тогда
— это точка пересечения
и
По
теореме о пропорциональных отрезках для параллельных прямых
и
угла
![]()
Отсюда получаем, что Кроме того,
как
половина диагонали куба с ребром
Тогда искомый отрезок равен
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан прямоугольный параллелепипед Точка
— центр грани
Сечения параллелепипеда плоскостями
и
являются
прямоугольниками,
и
— их меньшие стороны соответственно.
Известно, что
и
в 3 раза меньше соответственных больших сторон
прямоугольников.
а) Докажите, что — квадрат.
б) Найдите угол между прямой и плоскостью
Источники:
а) Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны.
Тогда плоскость пересекает плоскость верхнего основания по прямой,
параллельной
Пусть данная прямая пересекает
и
в точках
и
соответственно.
Плоскость пересекает плоскость верхнего основания по прямой,
параллельной
Пусть данная прямая пересекает
и
в точках
и
соответственно.
Пусть
Тогда по условию
Так как и
проходят через центр
прямоугольника
то имеем:
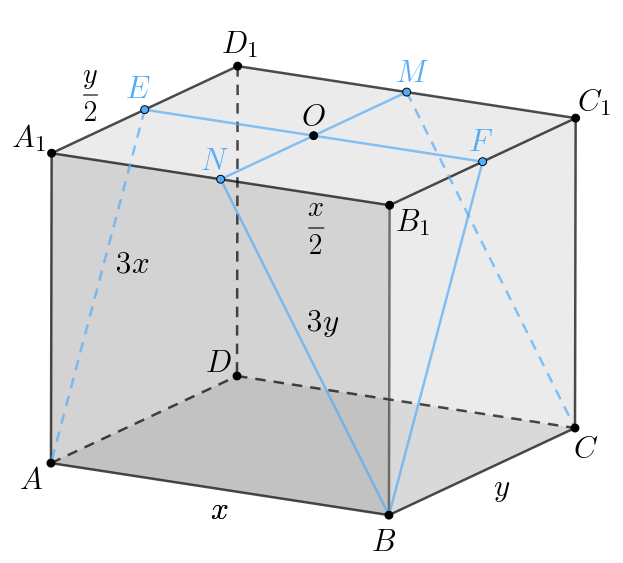
Так как — прямоугольный параллелепипед, то его
боковые ребра перпендикулярны основаниям. Тогда по теореме Пифагора для
прямоугольного треугольника
По теореме Пифагора для прямоугольного треугольника
Так как то получаем уравнение:
Получили, что значит,
— прямоугольник с равными
сторонами, то есть квадрат.
б) Проведем высоту в треугольнике
Заметим, что
то
есть
Также
так как
Тогда прямая
перпендикулярна двум пересекающимся прямым из плоскости
следовательно,
Тогда
перпендикулярна любой прямой из
плоскости
в частности
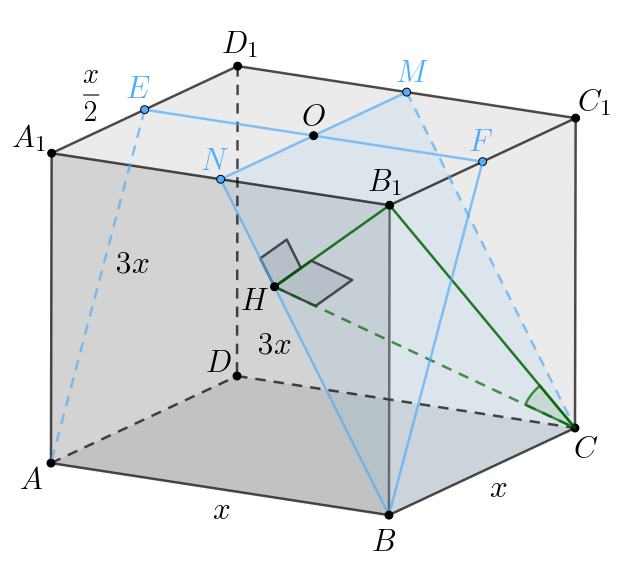
Получили, что
Следовательно,
и
— проекция точки
на плоскость
Тогда угол между прямой
и плоскостью
равен углу
Найдем его из прямоугольного
треугольника
Найдем Из пункта а) имеем:
По формуле высоты, проведенной к гипотенузе прямоугольного треугольника, получаем:
По теореме Пифагора для треугольника
Тогда из прямоугольного треугольника имеем:
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основанием прямой четырёхугольной призмы является квадрат
со стороной
высота призмы равна
Точка
— середина
ребра
Через точки
и
проведена плоскость
параллельная прямой
a) Докажите, что сечением призмы плоскостью является равнобедренный
треугольник.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью
Источники:
а) Рассмотрим треугольник По условию
— середина ребра
Через точку
проведем среднюю линию
параллельную стороне
Тогда точка
лежит в плоскости
так как эта плоскость параллельна прямой
Диагонали и
квадрата
точкой пересечения делятся
пополам, при этом
— середина
Значит,
и
пересекаются в
точке
Прямая проходит через точки
и
лежащие в плоскости
Следовательно, прямая
лежит в плоскости
значит,
—
искомое сечение.
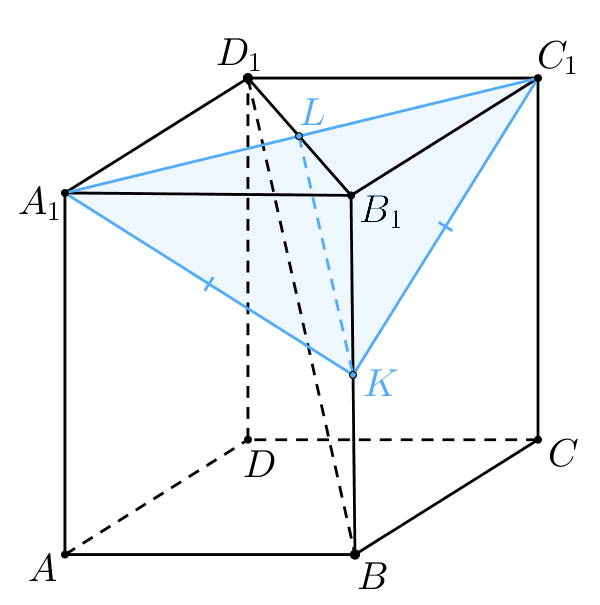
Рассмотрим прямоугольные треугольники и
У этих
треугольников катеты
и
равны как стороны квадрата
а
катет
— общий. Значит,
по двум катетам. В равных
треугольниках соответственные элементы равны, поэтому
Следовательно, треугольник
— равнобедренный.
б) По теореме Пифагора в треугольнике
Значит,
По теореме Пифагора в треугольнике
Значит,
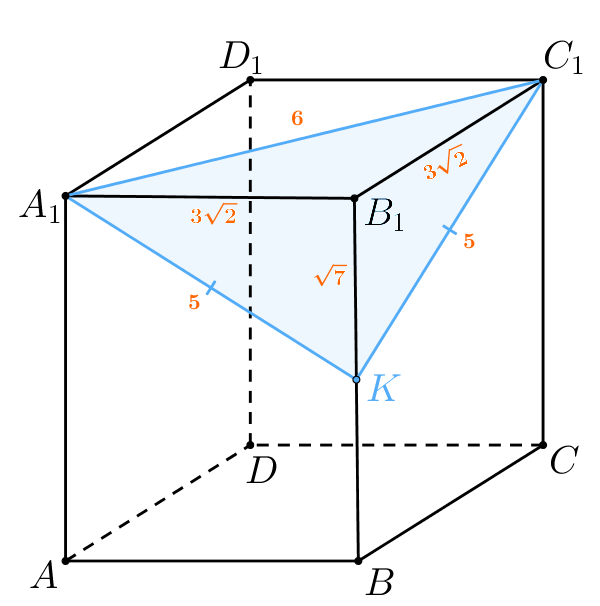
Тогда периметр треугольника
равен
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан куб Точки
и
— середины его ребер
и
соответственно. Плоскость
проходит через точку
параллельно прямым
и
а) Докажите, что плоскость проходит через точку
б) Найдите площадь сечения куба плоскостью если его ребра равны
2.
Источники:
а) Проведем через точку прямую параллельно
пусть это
Далее, поскольку
по построению и
по условию, то
— параллелограмм по определению. При этом
— середина
а
значит,
Получили, что — середина ребра
Пусть — центр нижнего основания. Тогда по свойствам квадрата в
основания куба получаем, что
и
Отсюда
— параллелограмм по признаку. Следовательно,
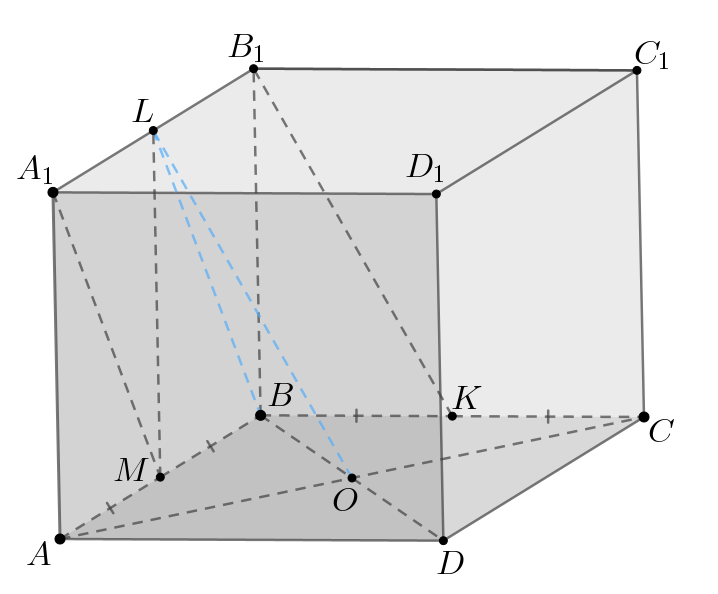
Таким образом, мы получаем, что плоскость содержит прямые
и
При этом
содержит отрезок
а значит и всю прямую, на которой он лежит.
Тогда прямая
лежит в плоскости
следовательно, точка
тоже
принадлежит
б) Пусть — середина
Поскольку плоскость сечения пересекает
нижнюю грань по прямой
то верхняя грань пересекается по прямой,
параллельной
а значит, и параллельной
При этом прямая
параллельна
поскольку является средней линией
Тогда
сечение куба плоскостью
— четырехугольник
По теореме Пифагора для
По теореме Пифагора для
Но известно, что и
Значит, получаем
Более того, они не могут быть параллельны в силу теоремы о трех попарно
пересекающихся плоскостях (
и
).
Таким образом, получаем, что — равнобедренная трапеция.
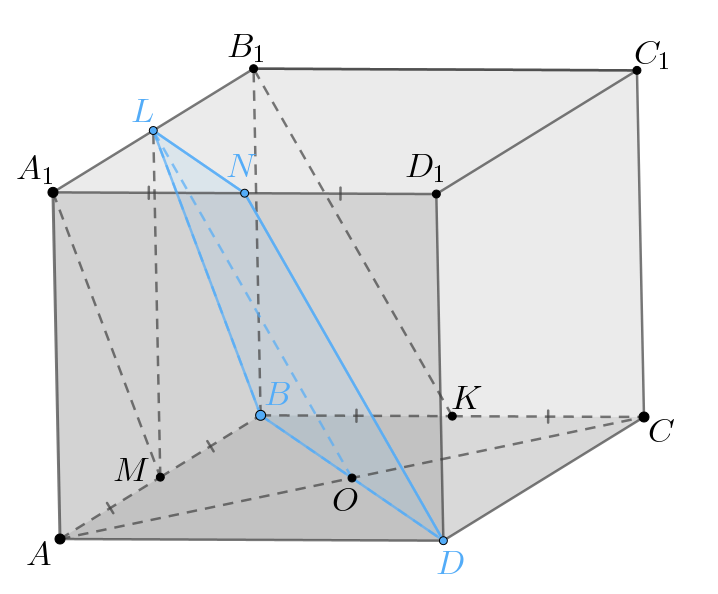
Заметим, что как средняя линия
Следовательно, по
теореме Пифагора для треугольника
получаем:
Кроме того, отрезок равен
как диагональ квадрата со стороной
2.
По теореме Пифагора для
Так как то мы знаем все стороны сечения. Более того,
так как данная трапеция равнобедренная, то она может быть вписана в
окружность. Значит, применима формула Брахмагупты для площади вписанного
четырехугольника. Для начала вычислим полупериметр:
Тогда имеем:
б) 4,5
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной призме отмечены точки
и
на ребрах
и
соответственно. Известно, что
и
– равнобедренная трапеция.
а) Докажите, что
б) Найдите объем призмы, если известно, что
Источники:
a) Пусть тогда
а
Спроецируем точку
на грань
в результате получим точку
—
середина
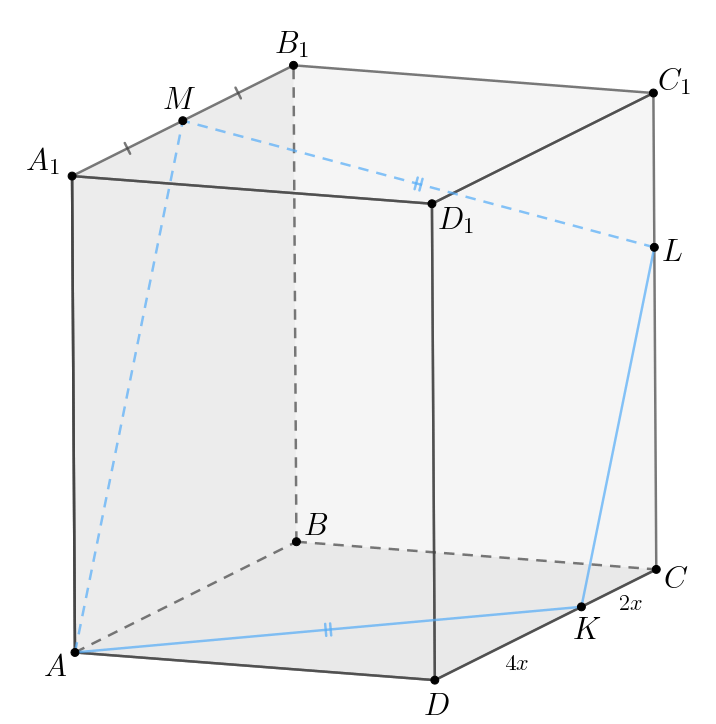
Рассмотрим грань проведем
и продлим
до пересечения с
продолжением стороны
пусть это пересечение происходит в точке
Заметим, что — параллелограмм, а значит,
а
поскольку
то

Треугольники и
подобны по двум углам (
как
накрест лежащие при параллельных прямых
и
и секущей
а
как вертикальные)
Запишем отношение соответствующих сторон
Что и требовалось доказать.
б) Так как то
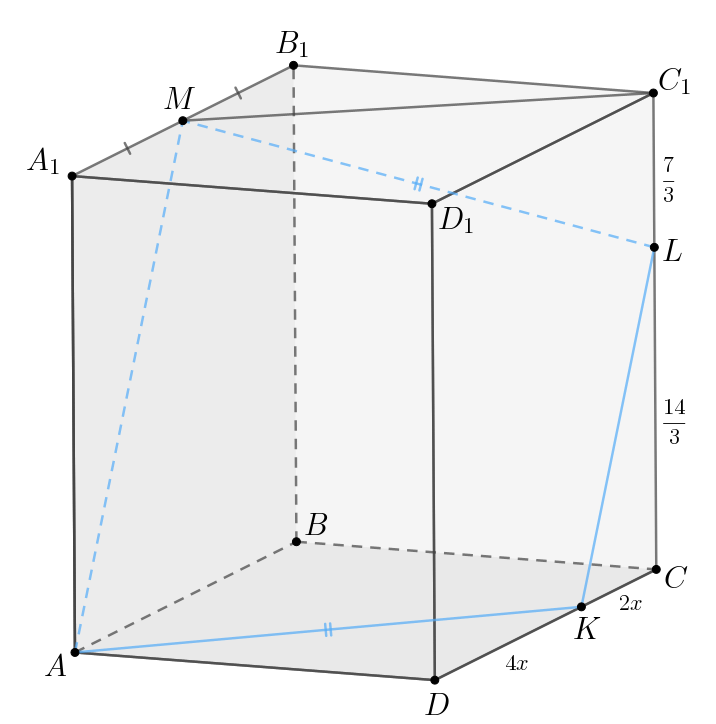
По теореме Пифагора для
По теореме Пифагора для
По теореме Пифагора для
Воспользуемся тем, что — равнобедренная трапеция, а значит,
Получаем уравнение:
Таким образом, у нас получилась правильная призма с высотой 7, а сторона
основания равна значит
б) 196
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде точка
лежит на ребре
Известно, что
Плоскость
проходит через точки
a) Докажите, что делит ребро
в отношении
считая от вершины
б) Найдите площадь сечения плоскостью если известно, что
Источники:
а) Из условия следует, что если принять то
Верхнее и нижнее основания параллелепипеда параллельны, следовательно,
плоскость пересечет их по параллельным отрезкам:
где
—
точка пересечения плоскости
с ребром
Аналогично для левой и правой
граней:
Таким образом, сечение параллелепипеда плоскостью
—
параллелограмм
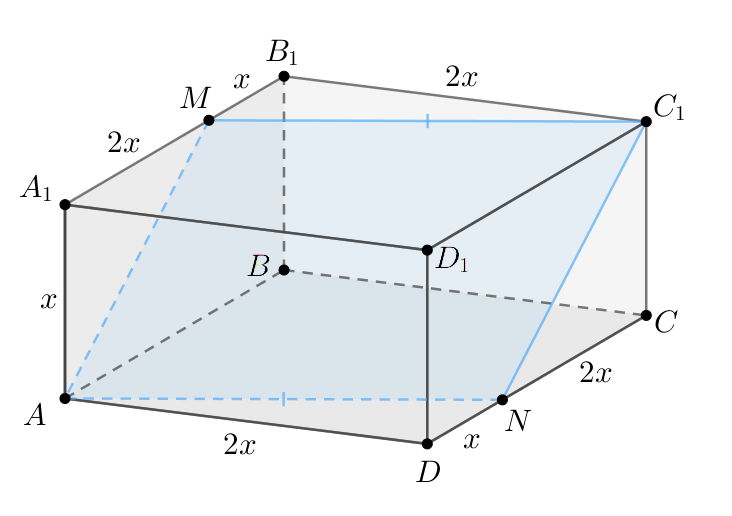
Тогда Следовательно,
по катету и
гипотенузе. Но тогда
Значит,
и
б) По условию
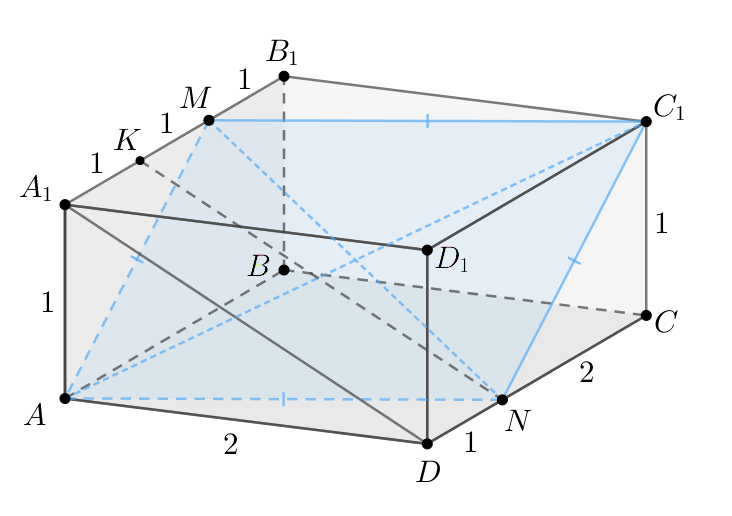
Заметим, что как гипотенузы равных прямоугольных треугольников
и
(эти треугольники равны по двум катетам). Следовательно,
сечение — ромб.
Тогда его площадь можно искать как
Пусть — середина
Тогда
и
Таким образом, площадь сечения равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде известно, что
Плоскость
проходит через вершины
и
и
пересекает ребро
в точке
такой, что
а) Докажите, что плоскость делит ребро
в отношении
б) Найдите площадь сечения параллелепипеда плоскостью
если
Источники:
а) Пусть тогда
Так как точки и
принадлежат плоскости сечения, то плоскость
пересекает нижнюю грань по отрезку
Значит, верхняя грань пересекается по
прямой, параллельной отрезку
Пусть плоскость
пересекает ребро
в точке
Спроецируем точку на верхнюю грань, пусть это будет точка
Тогда
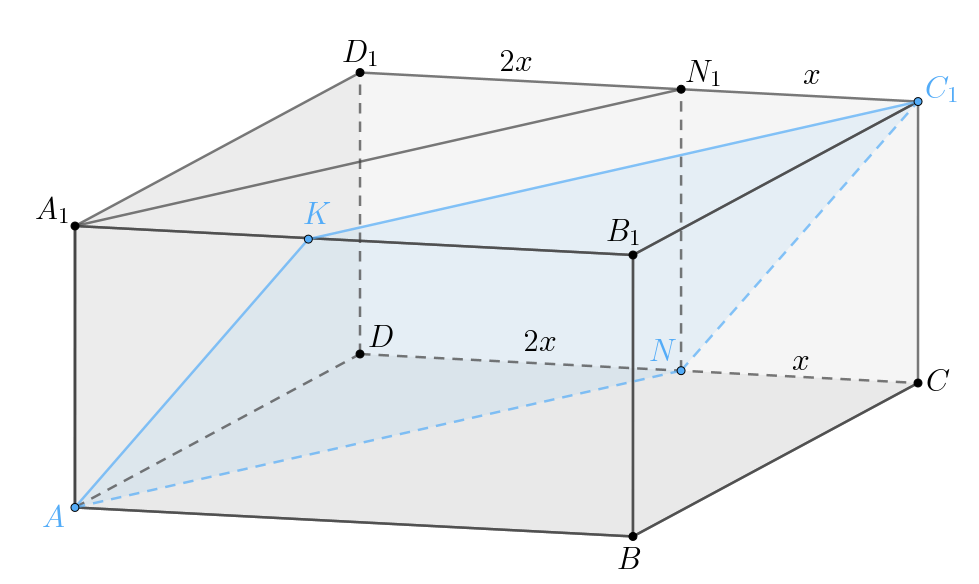
Заметим, что — параллелограмм, так как его противолежащие
стороны попарно параллельны. Значит,
и
Отсюда получаем
Что и требовалось доказать.
б) Так как то
Согласно пункту а), сечением параллелепипеда плоскостью является
параллелограмм
По теореме Пифагора для
По теореме Пифагора для
Спроецируем точку на нижнее основание, пусть это будет
Тогда
По теореме Пифагора для
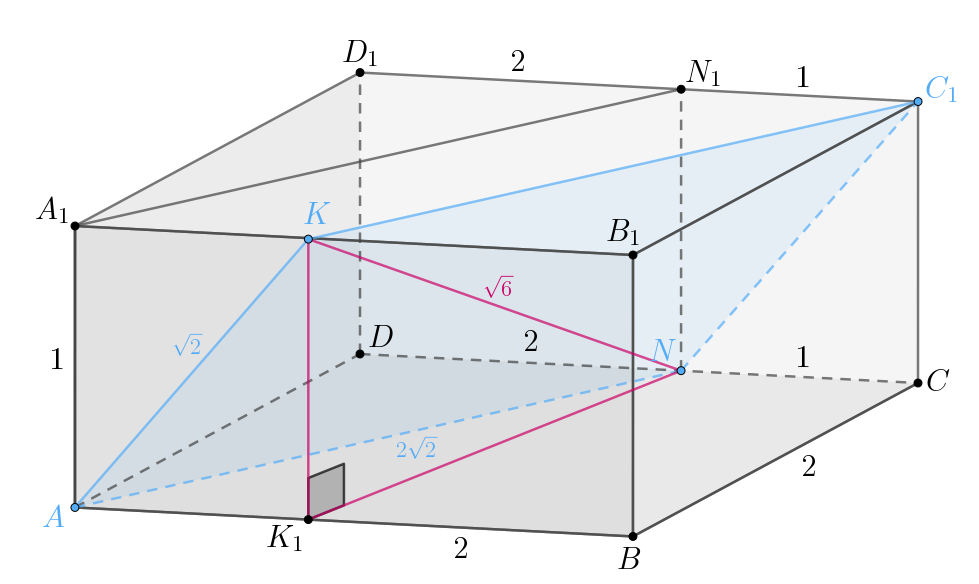
Тогда из теоремы косинусов для
Таким образом, площадь сечения равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



