№17 из ЕГЭ 2025
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Дан остроугольный треугольник Известно, что
Точка
— центр описанной окружности треугольника
Вокруг треугольника
описана окружность, которая пересекает сторону
в точке
a) Докажите, что треугольники и
подобны.
б) Найдите если
и
Источники:
a) Пусть тогда
Так как — центр описанной окружности, а
является вписанным и
опирается на хорду
тогда
как центральный, опирающийся на
хорду
Заметим, что так как — вписанный, то
Тогда по двум углам (
и
—
общий). Что и требовалось доказать.

б) Запишем отношение соответствующих сторон для
Заметим, что из подобия треугольников вытекает, что а значит,
является биссектрисой
По свойству биссектрисы получаем:
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан остроугольный треугольник Известно, что
Точка
— центр описанной окружности треугольника
Вокруг треугольника
описана окружность, которая пересекает сторону
в точке
a) Докажите, что треугольники и
подобны.
б) Найдите если
и
Источники:
a) Пусть тогда
Так как — центр описанной окружности, а
является вписанным и
опирается на хорду
тогда
как центральный, опирающийся на
хорду
Заметим, что так как — вписанный, то
Тогда по двум углам (
и
—
общий). Что и требовалось доказать.

б) Запишем отношение соответствующих сторон для
Заметим, что из подобия треугольников вытекает, что а значит,
является биссектрисой
По свойству биссектрисы получаем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В треугольнике проведены высота
и медиана
угол
равен
Точка
лежит на отрезке
В треугольнике
проведена высота
Прямые
и
пересекаются в точке
Известно, что
—
биссектриса угла
а) Докажите, что треугольник — прямоугольный.
б) Найдите площадь треугольника если
Источники:
а) Пусть Тогда из прямоугольного
с углом
получаем,
что
Рассмотрим прямоугольный Так как
то
В силу того, что
— биссектриса, получаем
Заметим, что по острому углу и гипотенузе. Тогда
следовательно, в силу
получаем
Таким образом, получили, что высота треугольника
является
и медианой, а значит, также является биссектрисой. Следовательно,

Тогда имеем:
Что и требовалось доказать.
б) В прямоугольном треугольнике катет напротив угла
равен
половине гипотенузы, тогда из
следует, что
Отсюда
и
Осталось найти отрезок так как он является высотой к стороне
в
Далее, как вертикальные. Тогда
по
острому углу и прилежащему катету. Отсюда
По теореме Пифагора для
Тогда искомая площадь равна:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике проведена высота
из вершины
прямого угла,
и
– биссектрисы треугольников
и
соответственно,
a) Докажите, что прямые и
перпендикулярны.
б) Найдите длину отрезка если
и
.
Источники:
а) Пусть и
пересекаются в точке
Заметим, что а значит, и половины данных углов равны, то
есть
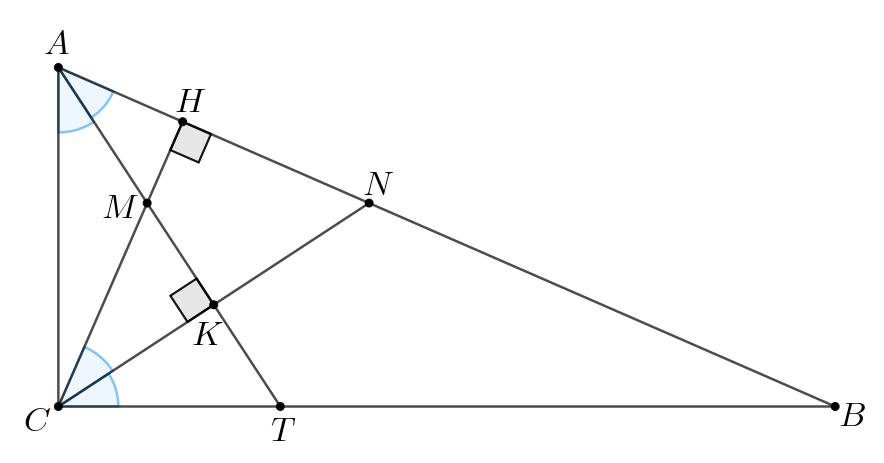
Тогда по двум углам (
,
как вертикальные). А значит,
б) Заметим, что в
является биссектрисой и высотой, а значит,
— равнобедренный. Тогда
Получаем, что — серединный перпендикуляр к стороне
а значит,
Аналогично, замечаем, что — биссектриса и высота в
следовательно, данный треугольник равнобедренный и
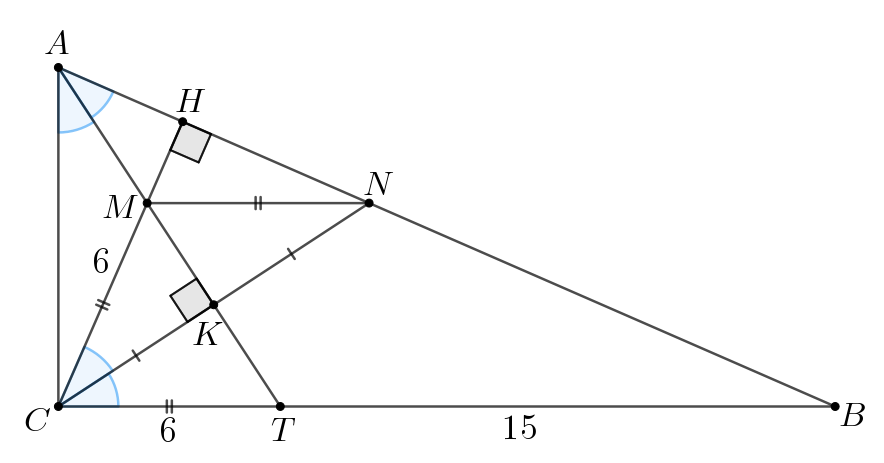
По свойству биссектрисы для
Таким образом, получаем, что
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В четырёхугольник вписана окружность с центром
Эта окружность
касается стороны
в точке
Известно, что
а) Докажите, что точка лежит на прямой
б) Найдите длину стороны если
Источники:
a) Поскольку — центр вписанной окружности, то он лежит на пересечении
биссектрис углов четырехугольника. Значит,
— биссектриса и
Пусть — радиус в точку касания, тогда
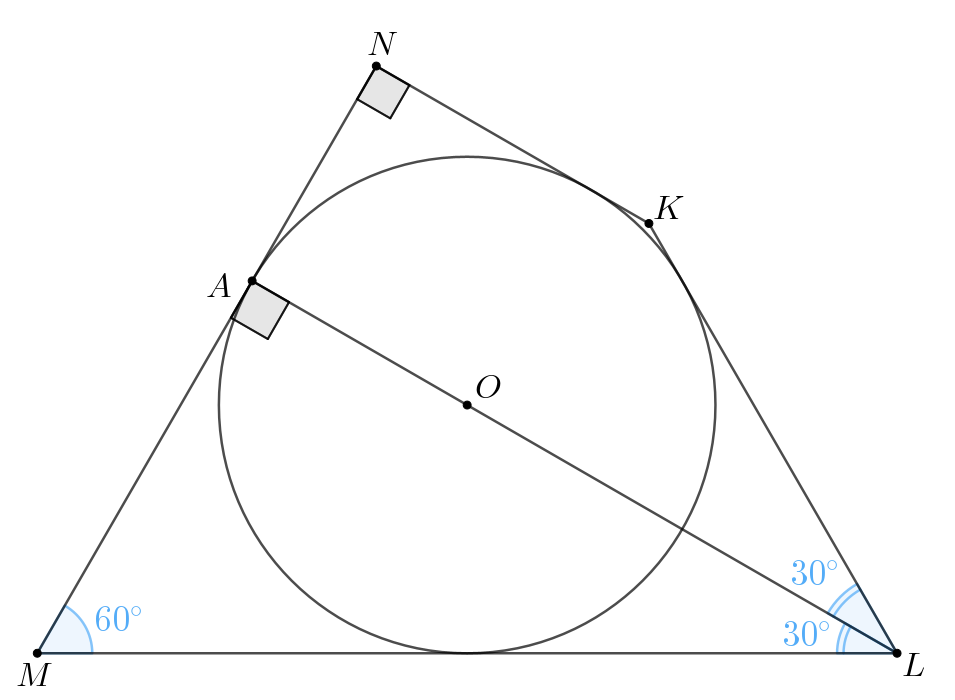
Предположим, что точка не лежит на
Тогда
— четырехугольник
и сумма его углов равна
Таким образом, получили, что — развернутый, а значит, точка
попадает на прямую
б) Из прямоугольного имеем:
Пусть тогда
Пусть окружность касается стороны
в точке
Заметим, что — квадрат, поэтому
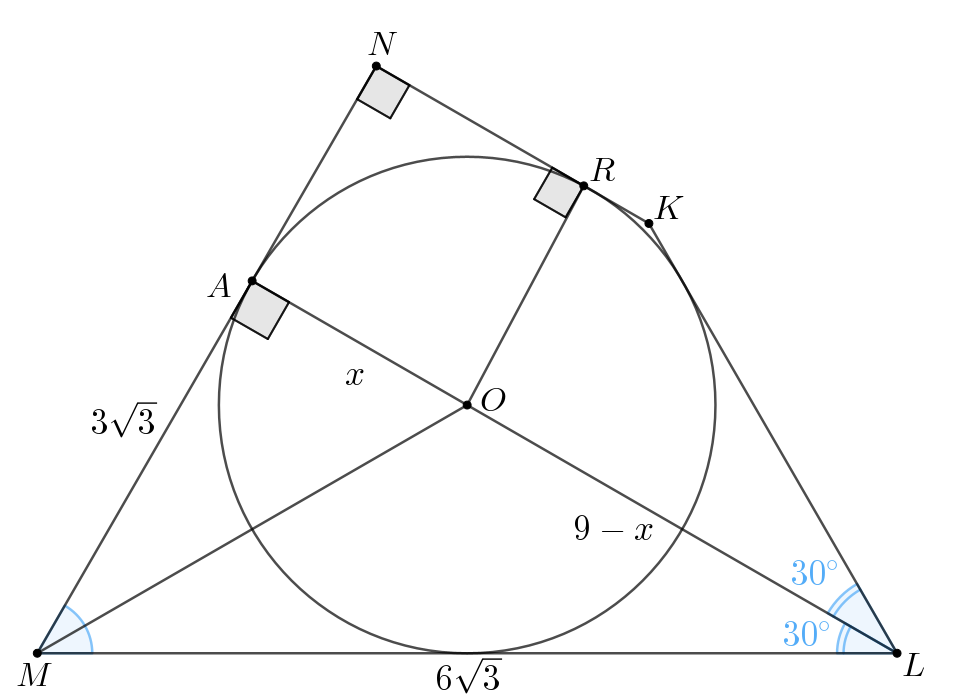
Поскольку — биссектриса, то по свойству биссектрисы получаем:
Таким образом, имеем Тогда искомая длина
равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В четырёхугольник вписана окружность с центром в точке
. Эта
окружность касается стороны
в точке
Известно, что
.
a) Докажите, что точка лежит на прямой
б) Найдите длину стороны если
Источники:
a) Так как окружность вписана в четырёхугольник, то её центр лежит на
пересечении его биссектрис, а значит — биссектриса угла
и
.
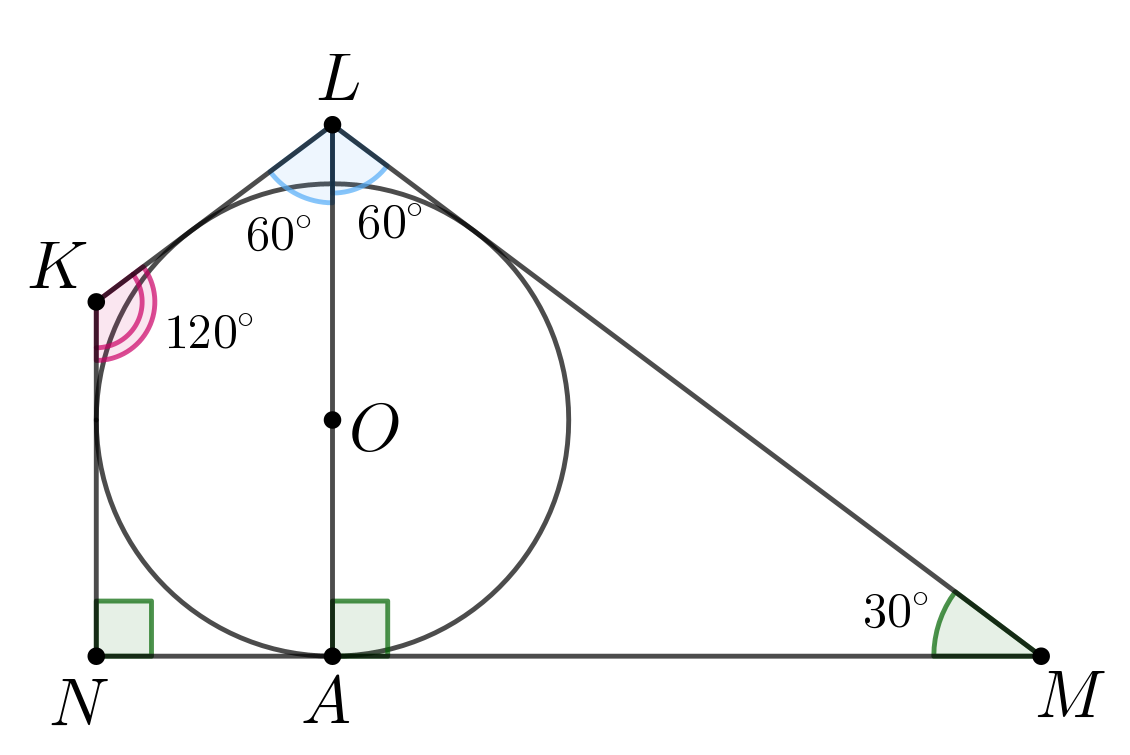
Так как сумма углов четырёхугольника равна
то:
Так как — радиус в точку касания,
Пусть Точка
не
лежит на прямой
Тогда
— четырёхугольник, и сумма его углов
равна
А так как угол то точки
лежат на одной прямой.
б)
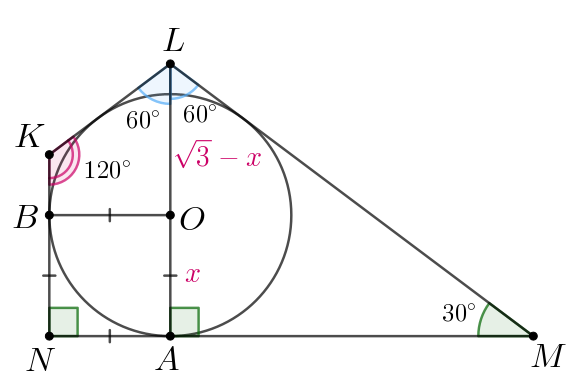
Так как катет против угла в равен половине гипотенузы, то в
прямоугольном треугольнике
имеем
По теореме Пифагора откуда
Обозначим
как
Тогда
Так как окружность вписана в четырёхугольник, то центр окружности лежит
на пересечении биссектрис, и — биссектриса угла
Пользуемся
основным свойством биссектрисы для треугольника
и биссектрисы
Пусть окружность касается стороны в точке
Тогда
—
квадрат и
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан параллелограмм c острым углом
В нем опущены высоты
и
на стороны
и
соответственно. На стороне
отмечена точка
так, что
Известно, что
а) Докажите, что
б) Найдите площадь треугольника если
Источники:
а) Пусть Тогда
по свойству параллелограмма
откуда также
Так как
и
—
односторонние, то
Тогда имеем:
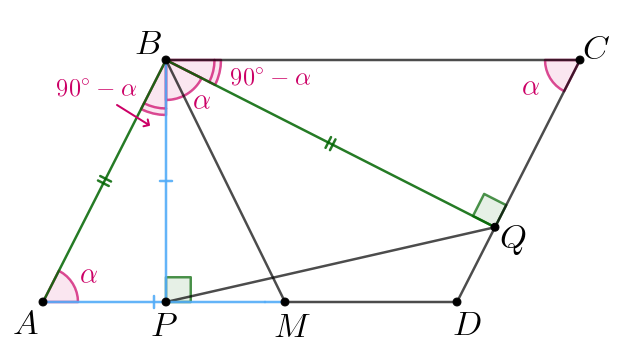
Тогда треугольники и
равны по двум сторонам
и
и углу между ними:
Отсюда получаем
Что и требовалось доказать.
б) По теореме Пифагора в треугольнике
Отсюда имеем:
Проведём в треугольнике высоту
Так как треугольники
и
равны, то их соответственные высоты
и
равны, а также
соответственные отрезки
и
равны.
Далее, так как и
то
Тогда длина высоты
из точки
к стороне
треугольника
равна длине перпендикуляра
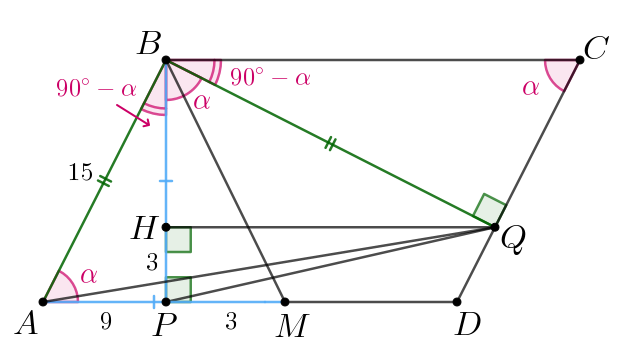
Тогда площадь треугольника равна:
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Биссектриса угла параллелограмма
пересекает его сторону
в
точке
Диагонали
и
параллелограмма пересекаются в точке
Окружность, описанная вокруг треугольника
касается прямых
и
а) Докажите, что
б) Отрезки и
пересекаются в точке
Найдите площадь
четырехугольника
если
Источники:
а) Заметим, что так как оба равны половине дуги
Тогда
в силу того, что
— биссектриса
получаем
Более того, заметим, что как накрест лежащие при
а значит,
— равносторонний. Кроме того,
так как оба равны половине дуги
Таким образом, получаем так как
и являются
накрест лежащими при прямых
и
и секущей
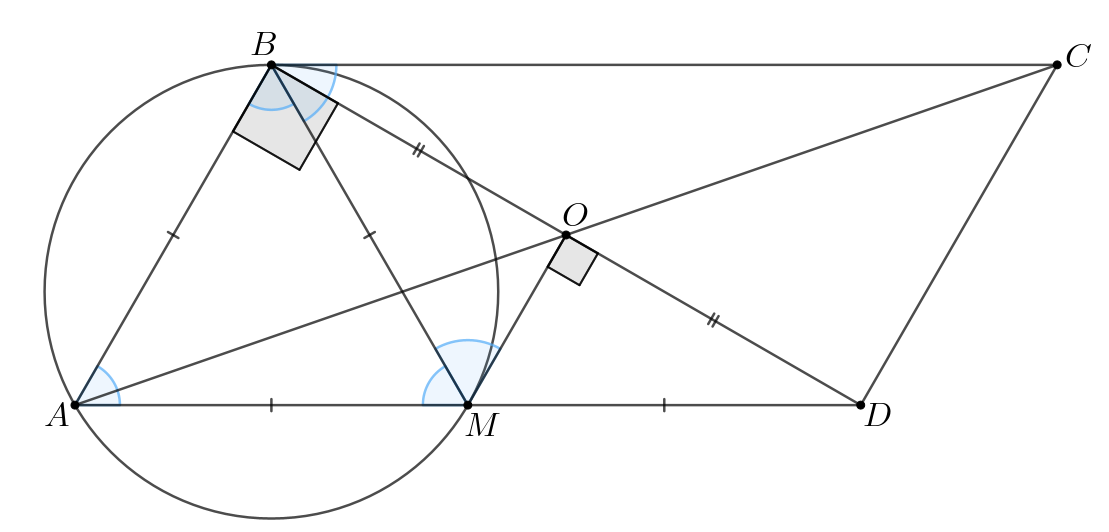
Тогда так как — середина
то
является средней линией
в
а значит,
Следовательно,
—
равнобедренный и медиана
к основанию является биссектрисой и высотой. В
частности получаем
По итогу получаем, что в силу параллельности
и
Что и
требовалось доказать.
б) Заметим, что
Так как — прямоугольный и
то
Следовательно,
так как катет, лежащий напротив угла
равен
половине гипотенузы.
По теореме Пифагора для
Тогда имеем:
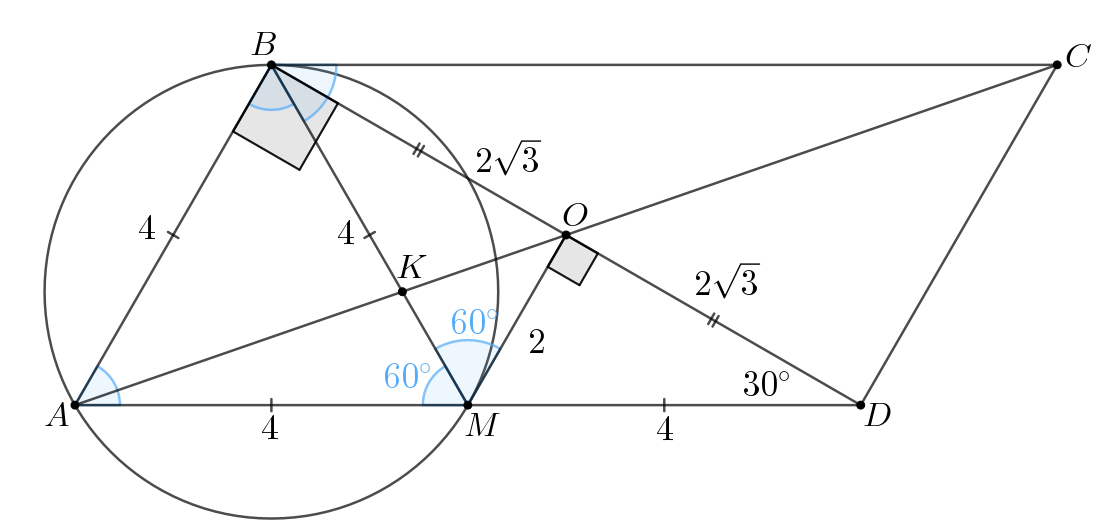
Заметим, что Найдем, в каком отношении точка
делит отрезок
и тогда сможем найти недостающую площадь
По теореме Менелая для и прямой
Таким образом, получаем
Тогда искомая площадь равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В четырёхугольник вписана в окружность с центром
Эта
окружность касается стороны
в точке
Известно, что
а) Докажите, что точка лежит на прямой
б) Найдите длину стороны если
Источники:
a) Поскольку — центр вписанной окружности, то он лежит на пересечении
биссектрис углов четырехугольника. Значит,
— биссектриса и
Пусть — радиус в точку касания, тогда
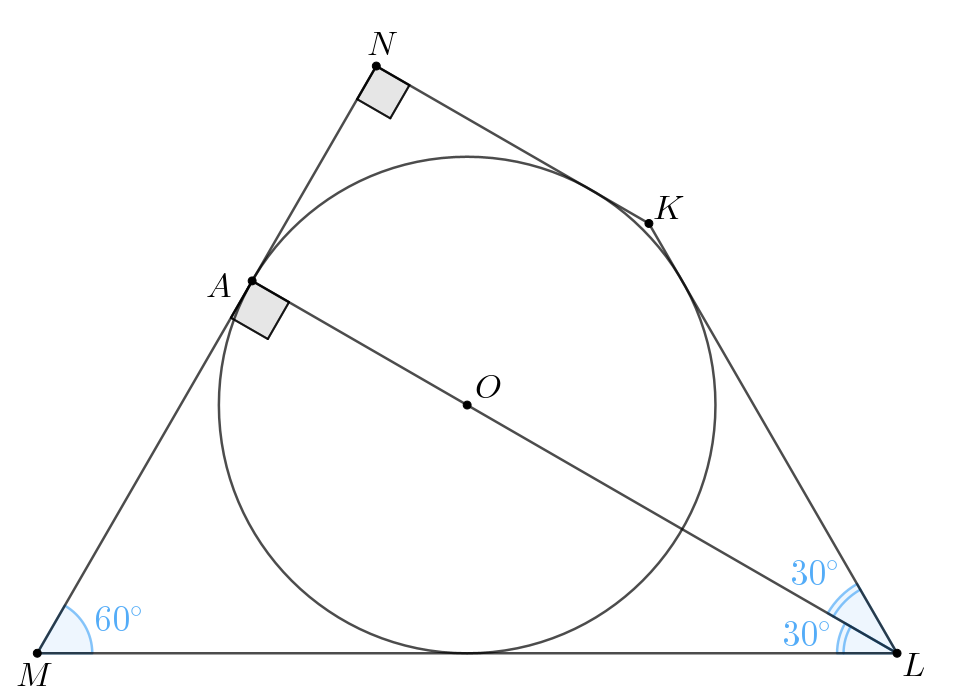
Предположим, что точка не лежит на
Тогда
— четырехугольник
и сумма его углов равна
Таким образом, получили, что — развернутый, а значит, точка
попадает на прямую
б) Из прямоугольного имеем:
Пусть тогда
Пусть окружность касается стороны
в точке
Заметим, что — квадрат, поэтому
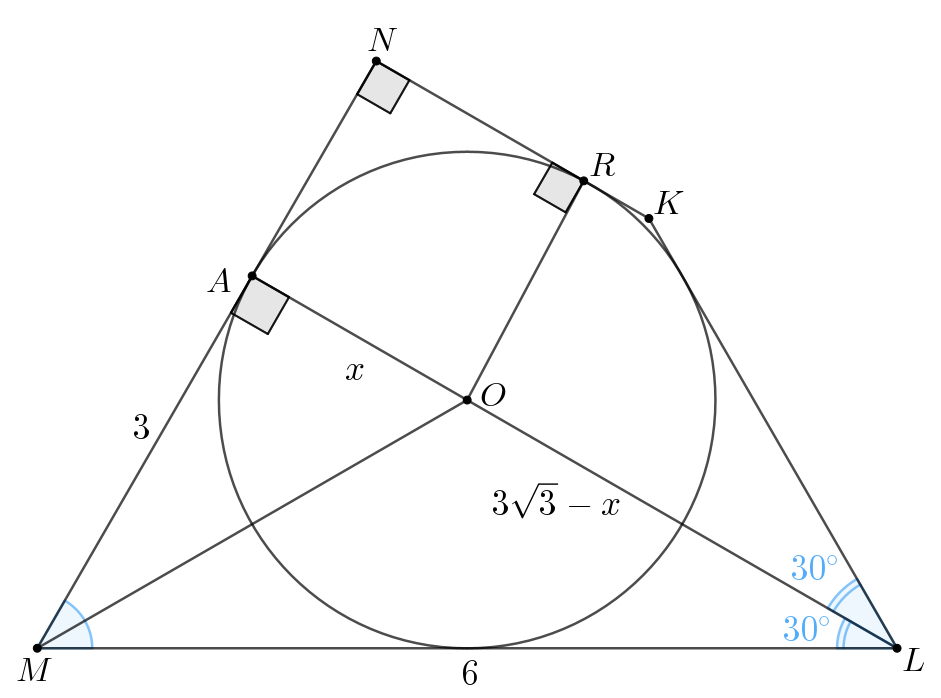
Поскольку — биссектриса, то по свойству биссектрисы получаем:
Таким образом, имеем Тогда искомая длина равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В четырёхугольник вписана в окружность с центром
Эта
окружность касается стороны
в точке
Известно, что
а) Докажите, что точка лежит на прямой
б) Найдите длину стороны если
Источники:
a) Поскольку — центр вписанной окружности, то он лежит на пересечении
биссектрис углов четырехугольника. Значит,
— биссектриса и
Пусть — радиус в точку касания, тогда
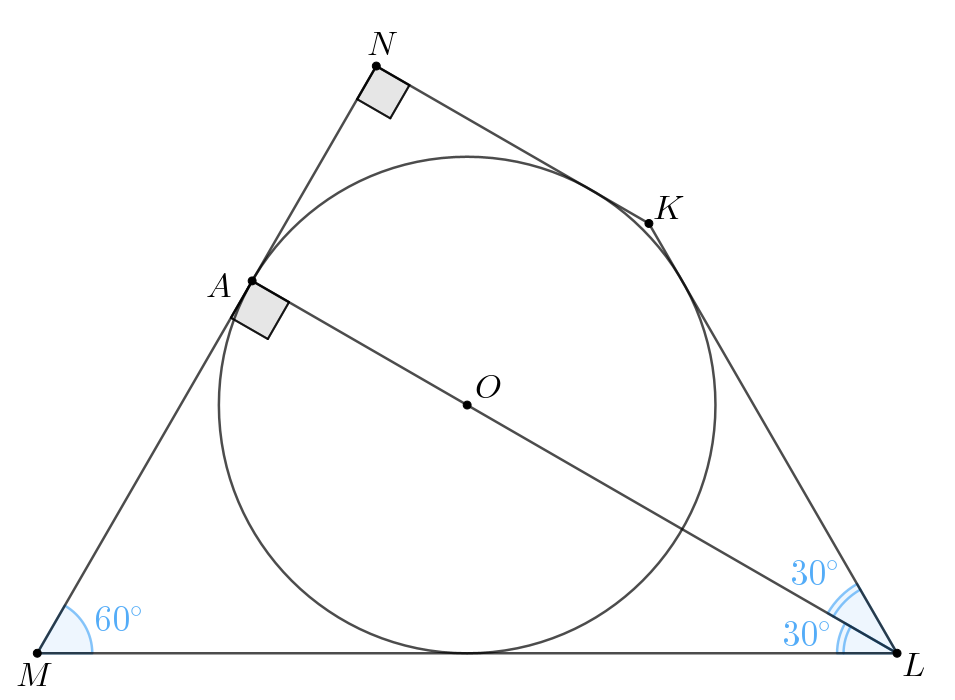
Предположим, что точка не лежит на
Тогда
— четырехугольник
и сумма его углов равна
Таким образом, получили, что — развернутый, а значит, точка
попадает на прямую
б) Из прямоугольного имеем:
Пусть тогда
Пусть окружность касается стороны
в точке
Заметим, что — квадрат, поэтому

Поскольку — биссектриса, то по свойству биссектрисы получаем:
Таким образом, имеем Тогда искомая длина равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В треугольнике проведены высота
и медиана
угол
равен
Точка
лежит на отрезке
В треугольнике
проведена высота
Прямые
и
пересекаются в точке
Известно, что
—
биссектриса угла
а) Докажите, что треугольник прямоугольный.
б) Найдите площадь треугольника если
Источники:
а) Пусть Тогда из прямоугольного
с углом
получаем,
что
Рассмотрим прямоугольный Так как
то
В силу того, что
— биссектриса, получаем
Заметим, что по острому углу и гипотенузе. Тогда
следовательно, в силу
получаем
Таким образом, получили, что высота треугольника
является
и медианой, а значит, также является биссектрисой. Следовательно,

Тогда имеем:
Что и требовалось доказать.
б) В прямоугольном треугольнике катет напротив угла
равен
половине гипотенузы, тогда из
следует, что
Отсюда
и
Осталось найти отрезок так как он является высотой к стороне
в
Далее, как вертикальные. Тогда
по
острому углу и прилежащему катету. Отсюда
По теореме Пифагора для
Тогда искомая площадь равна:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В треугольнике проведены высота
и медиана
угол
равен
Точка
лежит на отрезке
В треугольнике
проведена высота
Прямые
и
пересекаются в точке
Известно, что
—
биссектриса угла
а) Докажите, что треугольник — прямоугольный.
б) Найдите площадь треугольника если
Источники:
а) Пусть Тогда из прямоугольного
с углом
получаем,
что
Рассмотрим прямоугольный Так как
то
В силу того, что
— биссектриса, получаем
Заметим, что по острому углу и гипотенузе. Тогда
следовательно, в силу
получаем
Таким образом, получили, что высота треугольника
является
и медианой, а значит, также является биссектрисой. Следовательно,

Тогда имеем:
Что и требовалось доказать.
б) В прямоугольном треугольнике катет напротив угла
равен
половине гипотенузы, тогда из
следует, что
Отсюда
и
Осталось найти отрезок так как он является высотой к стороне
в
Далее, как вертикальные. Тогда
по
острому углу и прилежащему катету. Отсюда
По теореме Пифагора для
Тогда искомая площадь равна:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В треугольнике проведены высота
и медиана
угол
равен
Точка
лежит на отрезке
В треугольнике
проведена высота
Прямые
и
пересекаются в точке
Известно, что
—
биссектриса угла
а) Докажите, что треугольник — прямоугольный.
б) Найдите площадь треугольника если
Источники:
а) Пусть Тогда из прямоугольного
с углом
получаем,
что
Рассмотрим Так как
то
В силу того,
что
— биссектриса, получаем
Заметим, что по острому углу и гипотенузе. Тогда
следовательно, в силу
получаем
Таким образом, получили, что высота треугольника
является
и медианой, а значит, также является биссектрисой. Следовательно,

Тогда имеем:
Что и требовалось доказать.
б) В прямоугольном треугольнике катет напротив угла
равен
половине гипотенузы, тогда из
следует, что
Отсюда
и
Осталось найти отрезок так как он является высотой к стороне
в
Далее, как вертикальные. Тогда
по
острому углу и прилежащему катету. Отсюда
По теореме Пифагора для
Тогда искомая площадь равна:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
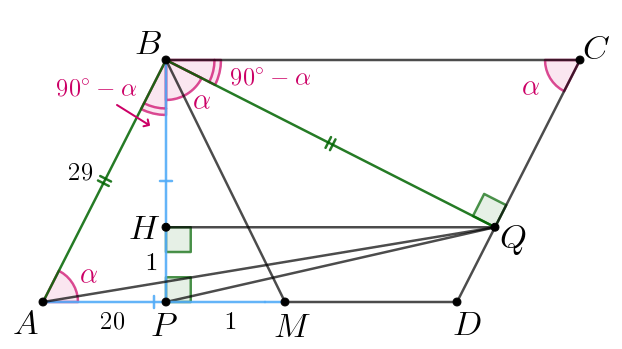
Дан параллелограмм c острым углом
В нем опущены высоты
и
на стороны
и
соответственно. На стороне
отмечена точка
так, что
Известно, что
а) Докажите, что
б) Найдите площадь треугольника если
Источники:
а) Пусть Тогда
по свойству параллелограмма
откуда также
Так как
и
—
односторонние, то
Тогда имеем:
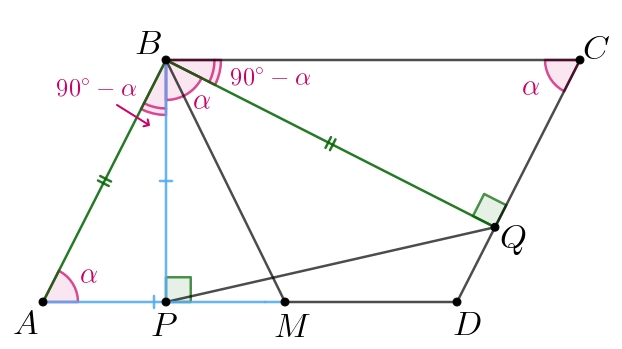
Тогда треугольники и
равны по двум сторонам
и
и углу между ними:
Отсюда получаем
Что и требовалось доказать.
б) По теореме Пифагора в треугольнике
Отсюда имеем:
Проведём в треугольнике высоту
Так как треугольники
и
равны, то их соответственные высоты
и
равны, а также
соответственные отрезки
и
равны.
Далее, так как и
то
Тогда длина высоты
из точки
к стороне
треугольника
равна длине перпендикуляра
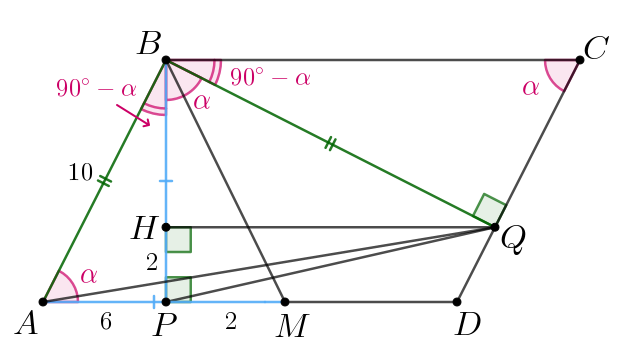
Тогда площадь треугольника равна:
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан параллелограмм c острым углом
В нем опущены высоты
и
на стороны
и
соответственно. На стороне
отмечена точка
так, что
Известно, что
а) Докажите, что
б) Найдите площадь треугольника если
Источники:
а) Пусть Тогда
по свойству параллелограмма
откуда также
Так как
и
—
односторонние, то
Тогда имеем:
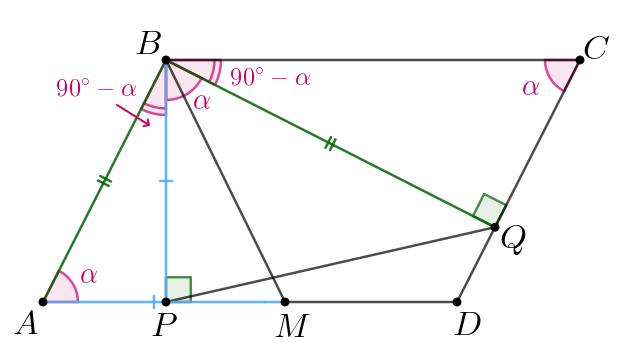
Тогда треугольники и
равны по двум сторонам
и
и углу между ними:
Отсюда получаем
Что и требовалось доказать.
б) По теореме Пифагора в треугольнике
Отсюда имеем:
Проведём в треугольнике высоту
Так как треугольники
и
равны, то их соответственные высоты
и
равны, а также
соответственные отрезки
и
равны.
Далее, так как и
то
Тогда длина высоты
из точки
к стороне
треугольника
равна длине перпендикуляра
Тогда площадь треугольника равна:
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В четырёхугольник вписана окружность с центром в точке
Эта
окружность касается стороны
в точке
Известно, что
a) Докажите, что точка лежит на прямой
б) Найдите длину стороны если
Источники:
a) Так как окружность вписана в четырёхугольник, то её центр лежит на
пересечении его биссектрис. Значит, — биссектриса угла
и
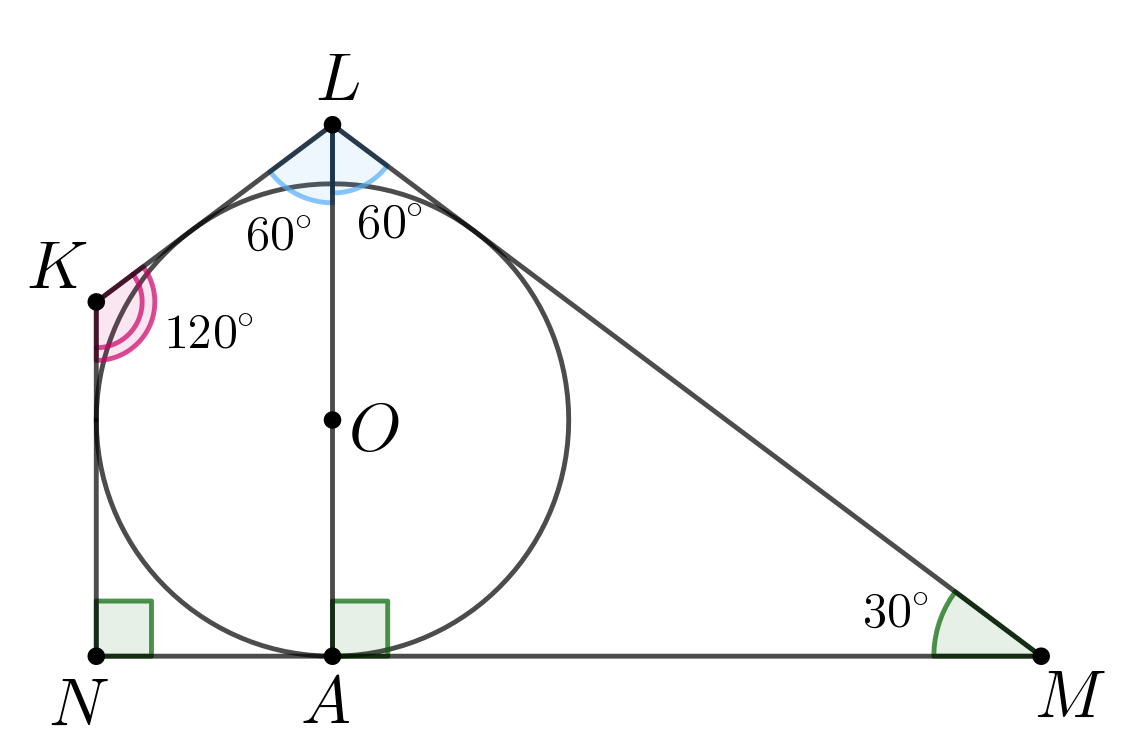
Так как сумма углов четырёхугольника равна
то
Пусть — радиус в точку касания, тогда
Пусть точка
не
лежит на прямой
Тогда
— четырёхугольник и сумма его углов равна
Тогда так как угол то точки
лежат на одной
прямой.
б)
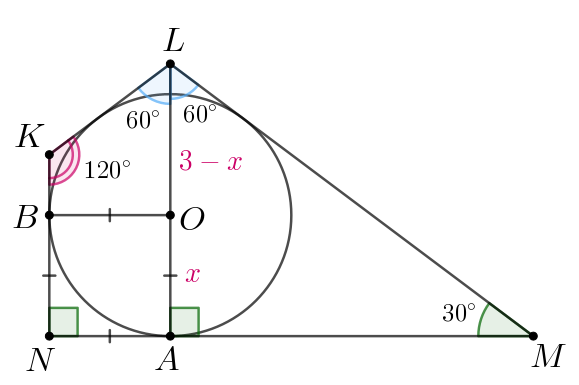
Так как в прямоугольном треугольнике катет напротив угла равен
половине гипотенузы, то в треугольнике
имеем
По теореме Пифагора для треугольника
Обозначим как
Тогда
Так как окружность вписана в четырёхугольник, то центр окружности
лежит на пересечении биссектрис и — биссектриса угла
Воспользуемся свойством биссектрисы для треугольника
и биссектрисы
Пусть окружность касается стороны в точке
Тогда
—
квадрат и
Тогда искомая длина равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В четырёхугольник вписана окружность с центром в точке
Эта
окружность касается стороны
в точке
Известно, что
a) Докажите, что точка лежит на прямой
б) Найдите длину стороны если
Источники:
a) Так как окружность вписана в четырёхугольник, то её центр лежит на
пересечении его биссектрис. Значит, — биссектриса угла
и
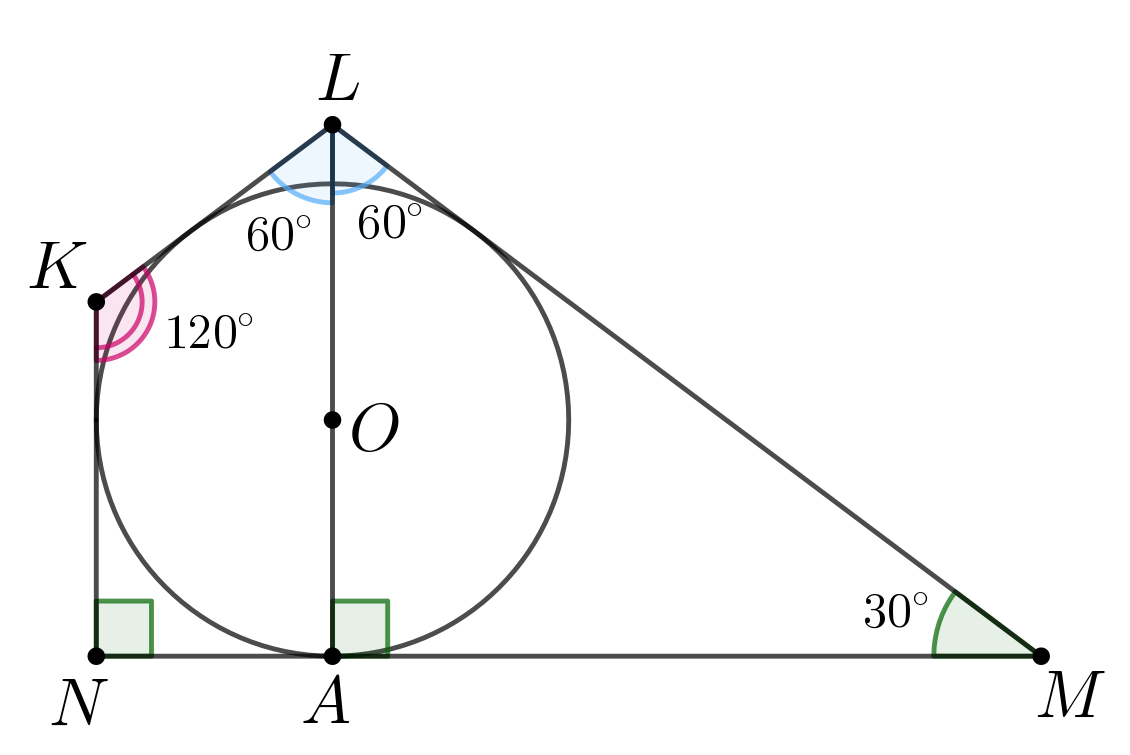
Так как сумма углов четырёхугольника равна
то
Пусть — радиус в точку касания, тогда
Пусть точка
не
лежит на прямой
Тогда
— четырёхугольник и сумма его углов равна
Тогда так как угол то точки
лежат на одной
прямой.
б) Так как в прямоугольном треугольнике катет напротив угла равен
половине гипотенузы, то в треугольнике
имеем
По теореме Пифагора для треугольника
Обозначим как
Тогда
Так как окружность вписана в четырёхугольник, то центр окружности
лежит на пересечении биссектрис и — биссектриса угла
Воспользуемся свойством биссектрисы для треугольника
и биссектрисы
Пусть окружность касается стороны в точке
Тогда
—
квадрат и
Тогда искомая длина равна
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
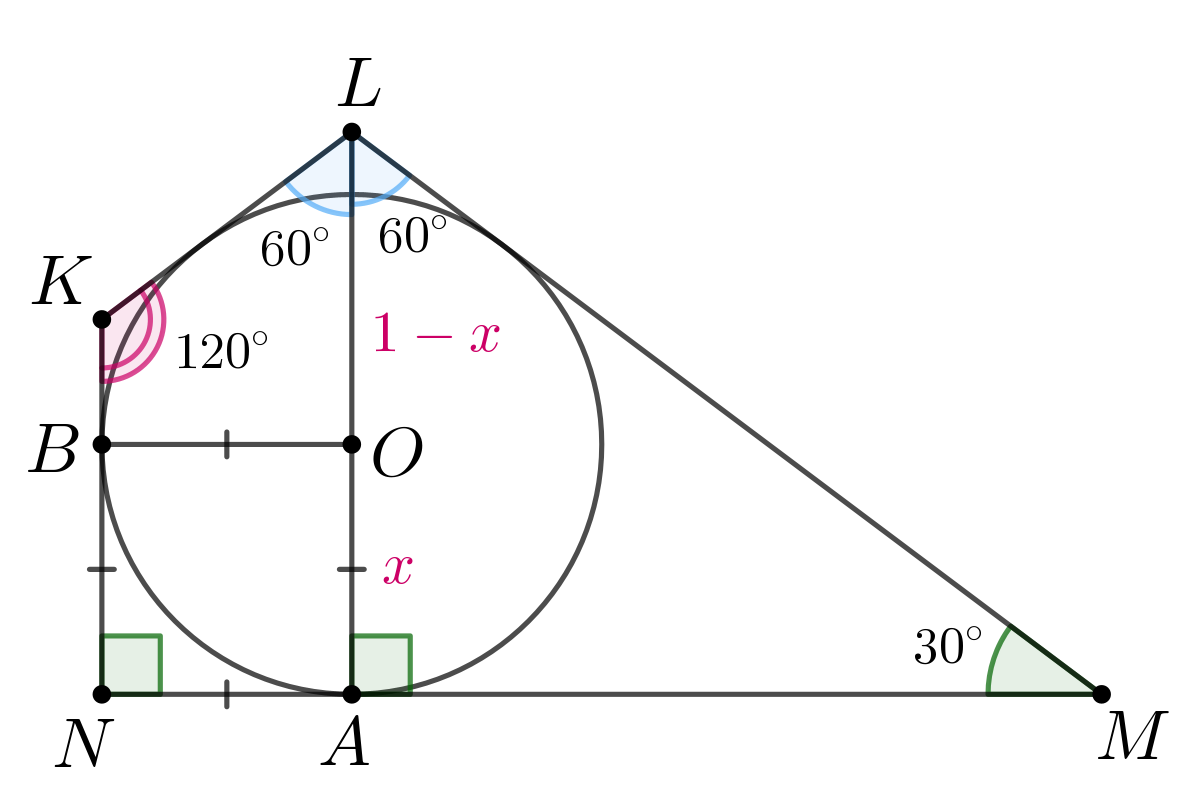
Сумма оснований трапеции равна 17, а её диагонали равны 8 и 15.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
Источники:
а) Обозначим вершины трапеции так, чтобы
было меньшим
основание,
— большим основанием.
Пусть а также
Выполним дополнительное
построение: через вершину
параллельно
проведем прямую до пересечения
с
в точке
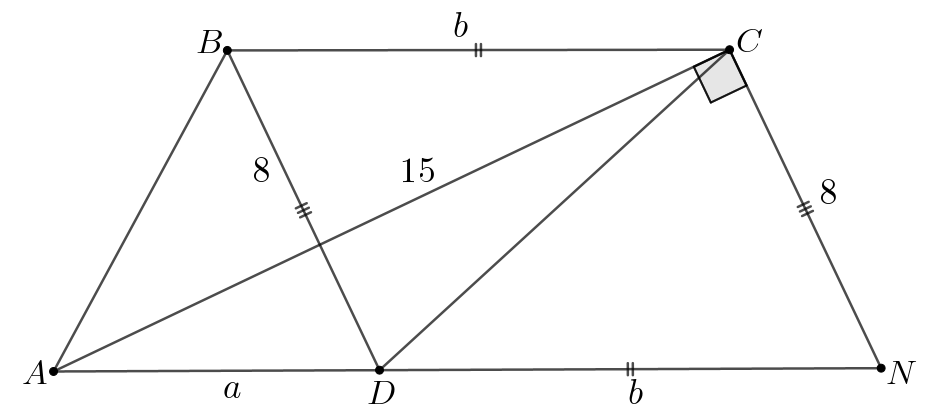
Заметим, что — параллелограмм по определению, а значит,
Таким образом, мы получили, что
Рассмотрим треугольник Заметим, что в нем
Действительно,
Таким образом, по обратной теореме Пифагора является
прямоугольным, то есть
Но так как данный угол получен в
результате параллельного переноса одной из диагоналей, то диагонали тоже
перпендикулярны.
б) Опустим высоту трапеции на прямую, содержащую основание
Заметим, что данная высота является ещё и высотой в прямоугольном
треугольнике
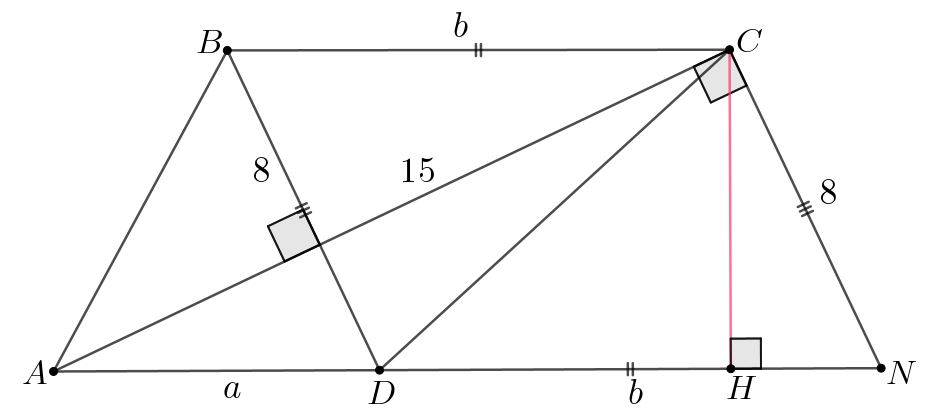
Площадь с одной стороны, равна
а с другой стороны,
равна
Тогда получаем
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан ромб Точки
и
— середины сторон
и
соответственно.
Проведены
и
таким образом, что они пересекают диагональ
в
точках
и
соответственно.
а) Докажите, что сумма площадей треугольников и
равна
площади треугольника
б) Известно, что в можно вписать окружность. Найдите радиус этой
окружности, если сторона ромба равна
Источники:
а) Так как — ромб, то диагонали точкой пересечения делятся
пополам.
Пусть — точка пересечения диагоналей, тогда
В треугольнике точка
— точка пересечения медиан, следовательно,
В треугольнике точка
— точка пересечения медиан, следовательно,
Пусть Из того, что
получаем:
Проведем диагональ Обозначим площадь ромба
за
Так как диагональ ромба разбивает его на два равных треугольника, то
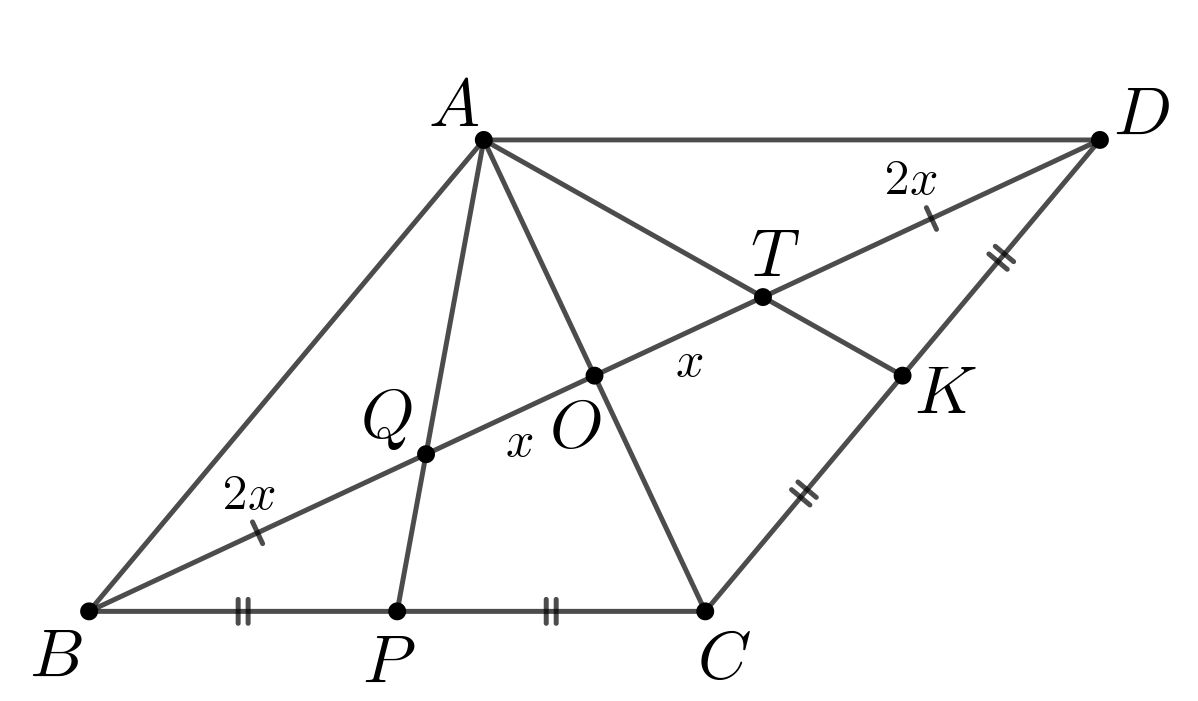
Далее, треугольники
и
имеют общую высоту из
вершины
тогда их площади относятся как длины оснований, к которым
проведена эта высота. Отсюда получаем:
Так как точка — точка пересечения медиан треугольника
то
Аналогично, так как точка — точка пересечения медиан треугольника
то
Кроме того, треугольники и
имеют общую высоту из вершины
а также треугольники
и
имеют общую высоту из вершины
Отсюда получаем:
Из этого следует искомое равенство:
б) По условию в пятиугольник можно вписать окружность. Значит, в
четырехугольник
вписана та же окружность, так как точка
— точка
пересечения продолжений сторон пятиугольника
и
Кроме того, та же
окружность вписана в треугольник
По свойству вписанной в четырехугольник окружности имеем:
Выразим отрезок и подставим известные значения:
Треугольник прямоугольный, так как диагонали ромба пересекаются
под прямым углом. По теореме Пифагора получаем:
Точка делит диагонали пополам, как точка пересечения диагоналей ромба.
Значит,
Треугольник прямоугольный, так как диагонали ромба пересекаются
под прямым углом. По теореме Пифагора получаем:
В треугольнике медианы
и
пересекаются в точке
следовательно,
Из этого получаем равенство:
Найдем площадь треугольника
Найдем полупериметр треугольника
Из формулы площади треугольника найдем радиус вписанной
окружности:
б) 4
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
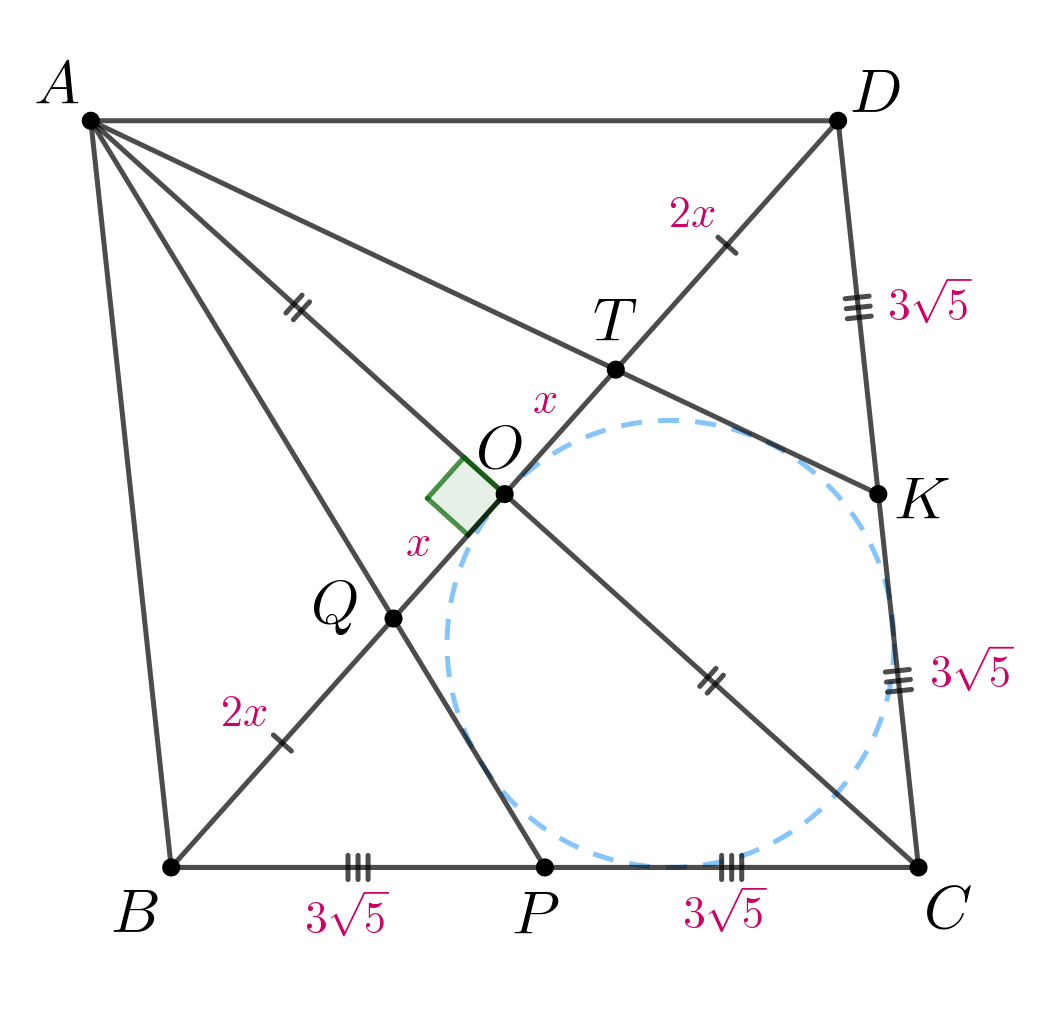
На стороне и диагонали
квадрата
отмечены точки
и
соответственно, при этом
а) Докажите, что точки лежат на одной окружности.
б) Найдите расстояние от точки пересечения диагоналей четырехугольника
до прямой
если сторона квадрата равна 132.
Источники:
а) Пусть Тогда
Пусть
Продлим прямую до пересечения со стороной
Пусть она пересекает
сторону
в точке
Тогда заметим, что
Причем коэффициент подобия равен а значит,
Через точку
проведем отрезок
параллельный стороне
причем
точка
принадлежит стороне
Тогда
и
Продлим прямую до пересечения со стороной
Пусть она пересекает
сторону
в точке
Тогда заметим, что
Причем коэффициент подобия равен а значит,
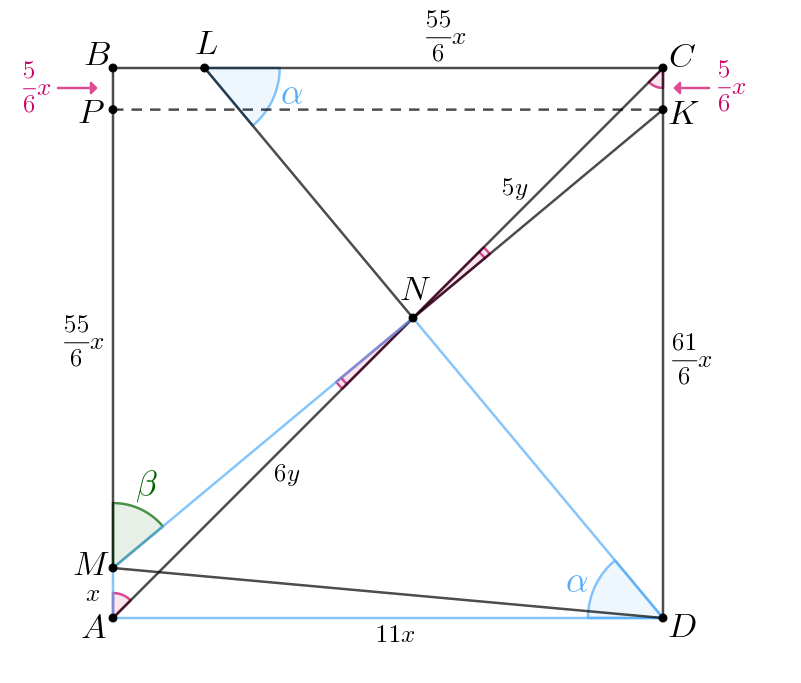
Заметим, что прямоугольные треугольники и
равны по двум
катетам, а значит, имеет место равенство:
Таким образом, Тогда
Следовательно, четырехугольник
— вписанный.
б) Заметим, что а значит, в силу вписанности четырехугольника
получаем, что
Пусть и
пересекаются в точке
Опустим перпендикуляр
на
сторону
Заметим, что
— биссектриса угла
следовательно, имеет
место равенство:
Заметим, что по двум углам, так как
— общий и
Тогда
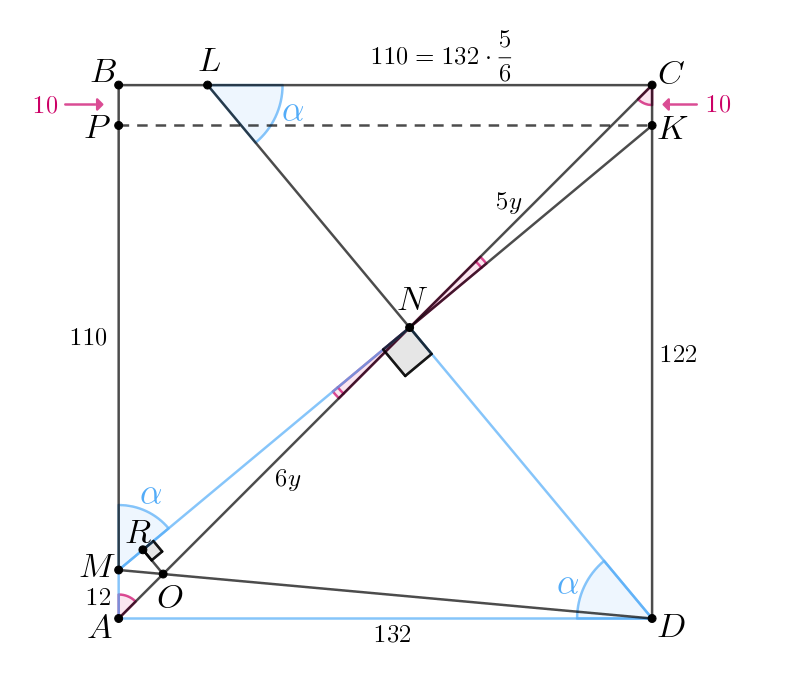
Так как и коэффициент подобия равен
то получаем,
что
Таким образом, используя теорему Пифагора для окончательно
имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а), и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



