Тема ПВГ - задания по годам

ПВГ 2020

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела пвг - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#31185

Решите систему

({ ∘ x- ∘-y -7- √y + x = √xy√ +-1; ( x xy+ 78= −y xy.

Источники: ПВГ-2020

Подсказки к задаче

Подсказка 1

Перенеся во втором уравнении правую часть налево, а 78 - направо, подумаем, что нужно сделать, чтобы сверху тоже получилось это выражение.

Подсказка 2

Конечно, напрашивается умножить на ху первое уравнение, только нужно рассмотреть два случая: когда 1) x>0 y>0 или 2) x<0 y<0, чтобы верно произвести умножение с корнями

Подсказка 3

Важно подметить, что в 1 случае sqrt(х^2) будет равен х, а во втором этот же корень равен -х. Эти два случая приведут к квадратным уравнениям относительно t = sqrt(xy), к решениям которых мы потом применим обратную замену и найдем ответ.

Показать ответ и решение

Область определения системы распадается на две подобласти: $1) x,y > 0$ и $2) x,y < 0$ .

При умножении первого уравнения на $xy ⁄= 0$ , получаем

∘ x- ∘ y- √-- x⋅(y⋅ y)+ y⋅(x⋅ x)= 7 xy+ xy

В подобласти $(1)$ верно $∘-- √-- y = y2,x = x2$ , то есть мы можем занести под корень и сократить:

{ √-- √-- √-- x xy+ y-xy =7 xy +xy x√xy+ 78= −y√xy

откуда следует, что число $√ -- t= xy$ удовлетворяет квадратному уравнению $t2 +7t+ 78 =0$ , которое решение не имеет.

В подобласти $(2)$ же из-за того, что $∘ -- √ -- y = − y2,x= − x2$ при занесении под корень в левой части появляются минусы перед корнями:

{ √ -- √ -- √ -- − x xy−√y-xy = 7 xy+√ xy; x xy +78= −y xy,

откуда следует, что число $√ -- t = xy$ удовлетворяет квадратному уравнению $2 t +7t− 78 =0$ , решениями которого являются $t1 = −13,t2 = 6$ .

Так как $t> 0$ , то с учетом исходной системы получаем $x⋅y =36,x+y = −13.$ В итоге имеем две пары решений $(− 9;−4),(−4;−9)$ .

Ответ:

$(−9;−4),(−4;−9)$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#32375

Решите систему

{ − ctg xctgy− ctgy +|ctgx − ctgy− 3ctgxctgy|=0; √3−-tgx-+tgy+ tg y− 5 =0.

Источники: ПВГ - 2020, 11.4 (pvg.mk.ru))

Подсказки к задаче

Подсказка 1

Посмотрите на эту систему. Что в этой системе кажется наиболее инородным? Модуль. Что мы привыкли делать с ним? Раскрывать по определению(чаще всего именно так, потому что работать напрямую с модулем, зачастую, затруднительно). Сделайте тоже самое.

Подсказка 2

Если раскрыть модуль с минусом, то из первого уравнения выходит, что либо ctg(x)=0 , либо ctg(y)=1/2. Но ctg(x)!=0, так как тангенс тоже должен быть определен. Поэтому ctg(y)=1/2. Значит tg(y)=2. Подставляя это во второе уравнение найдем первую серию решений(не забывая проверить то, что модуль был раскрыт верно и ОДЗ выполнено). Теперь осталось раскрыть модуль другим способом.

Подсказка 3

Второй случай не дает ответов сразу. У нас получается выражение, где все завязано на котангенсах, но при этом, если мы планируем в явном виде подставить выражение, к примеру , tg(x) во второе уравнение, то нам надо связь из котангенсов переделать в связь на тангенсы. Как это сделать?

Подсказка 4

Для начала, можно выразить ctg(y) через ctg(x), а потом перевернуть дробь(которая будет получена при выражении ctg(y) ) и заменить ctg(x) на 1/tg(x). И получим в явном виде , выраженное через tg(x), значение tg(y) . Остается подставить это во второе уравнение и найти его корни, после чего проверить так ли мы раскрыли модуль и учесть ОДЗ.

Показать ответ и решение

Из второго уравнения на ОДЗ следует, что $− tgx= tg2y − 11tgy+ 22 (∗)$ .

Раскроем модуль одним способом:

− ctgxctgy− ctgy− (ctgx− ctgy − 3ctgxctgy)= − ctgxctg y− ctgx+ 3ctgxctgy = 0

$ctgx ⁄=0$ , поэтому $2ctgy =1$ . Значит, $tgy =2$ . Подставим это во второе уравнение:

∘ ------ 5− tgx− 3= 0

Тогда $tgx = −4$ . Осталось подстановкой проверить, что для полученного решения модуль был раскрыт верно.

Теперь раскроем модуль другим способом.

− ctgxctgy − ctgy+ (ctgx− ctgy− 3ctgx ctgy)=

=− 4ctgxctgy− 2ctgy+ ctgx =0

Домножим на $tg xtgy$ :

−4 − 2tgx+ tgy = (∗)= −4+ 2(tg2y− 11tgy +22)+tgy =

=2tg2y− 21tgy +40= (tgy − 8)(2tgy− 5)= 0

Если $tgy = 8$ , то $2 tgx= −(tg y− 11tgy+ 22)= 2$ и при подстановке это не подходит.

Если $tgy = 2.5$ , то $2 tgx= −(tgy − 11tgy+ 22)= −0.75$ и при подстановке это не подходит.

Ответ:

$(− arctan4+ πn;arctan2 +πk), n∈ ℤ,k∈ ℤ$

Ошибка.
Попробуйте повторить позже

Задача 3#39866

Найдите все значения параметра $a$ , при каждом из которых уравнение

2 x + a|x− a|=8x − 15

имеет решение. Для каждого из найденных значений укажите число решений уравнения.

Источники: ПВГ-2020

Подсказки к задаче

Подсказка 1

Первое, что надо заметить в этой задаче, — это то, что, кажется, она нормально не решается аналитически. Значит, наверное, можно решить её графически! Если сделать одно преобразование, станет понятно, почему и как задача решается графически!

Подсказка 2

Конечно, надо оставить слагаемые с параметром в одной части уравнения, а остальные перекинуть в другую. Тогда в одной части образуется уравнение параболы, а в другой — понятный график модуля! Построим график параболы, а также подумаем, как меняется график модуля при изменении параметра. Может, это натолкнёт нас на интервалы для параметра, которые стоит рассматривать...

Подсказка 3

При a < 0 ветви у модуля идут вниз, а при увеличении параметра они постепенно поднимаются вверх и становятся всё ближе друг к другу! Кроме того, при увеличении параметра вершина модуля (a; 0) движется по оси абсцисс вправо. Тогда ключевыми точками будут a = 0, a = 3 и a = 5. Осталось только рассмотреть интервалы для параметра и в каждом из них узнать наличие решений, а также их количество :)

Показать ответ и решение

Уравнение можно переписать так:

2 a|x− a|= −x +8x− 15

График правой части представляет собой параболу $y =− x2+8x− 15$ ветвями вниз, пересекающую ось $Ox$ в точках $(3;0)$ и $(5;0)$ . Рассмотрим теперь график левой части $y = a|x− a|$ при разных значениях параметра.

$a <0$ . Имеем «галочку» ветвями вниз с вершиной в точке $(a;0)$ , правая ветка которой при данных значениях параметра пересекает параболу дважды.
$a =0$ . Горизонтальная прямая, совпадающая с осью $Ox.$ Пересечение нашли выше, получаем также два решения.
$0 <a <3$ . Ветви «галочки» направлены вверх, но только правая ветвь $x ≥a$ пересекается с параболой, поэтому решения есть только в случае
$a(x− a)= −x2+ 8x − 15,x− a≥0$

$x2+x(a− 8)+(15− a2)= 0,x ≥a$
Необходимо и достаточно проверить $x≥ a$ для меньшего корня, тогда будет выполнено и для большего
$8− a− ∘5a2−-16a-+4 ≥2a$

$∘ ---------- 8− 3a≥ 5a2 − 16a+ 4$

$(|{ 8− 3a≥0 5a2− 16a+ 4≥ 0 |( 64− 48a+ 9a2 ≥ 5a2− 16a+4$

$( 8 ||{ a≤ 3( 8−2√11] [8+2√11 ) || a∈ 0;--5---∪ ---5--;3 ( 4a2− 32a+ 60≥ 0 ⇐ ⇒ a∈(−∞, 3]∪ [5,+∞ )$
После пересечения остаётся только $( √--] a∈ 0;8−-2511-,$ потому что $√-- 8+25-11-> 8∕3.$
$a =3,a= 5$ . В каждом случае ровно одно решение, поскольку коэффициенты наклона ( $3$ и $5$ ) больше модулей наклона касательных в $x= 3$ и $x= 5$ , которые равны $1.$
$3 <a <5$ . Здесь ветви направлены вверх и каждая пересекает дугу параболы выше оси абсцисс, то есть всегда два решения.
$a >5$ . Решаем аналогично $0 <a <3$ , здесь $x≤ a$ , потому что пересекать может только левая ветка галочки.
$2 2 x − (a+ 8)x+ 15+ a = 0$
Решения могут быть только при неотрицательном дискриминанте
$[ √-- √--] − 3a2+ 16a+4 ≥0 ⇐ ⇒ a ∈ 8−-2-19,8+-2-19 3 3$

$( 8+2√19] a∈ 5,--3----$
Проверим $x ≤a$ для большего корня (для меньшего тогда тоже выполнится)

$8+ a+∘ −3a2+-16a-+4≤ 2a ⇐⇒ ∘−-3a2-+16a+-4≤ a− 8$
Должно быть $a≥ 8$ , но уже это неверно для полученного полуинтервала для неотрицательного дискриминанта. В итоге в этом случае решений нет.

Ответ:

$a ∈(−∞; 8−2√11]∪ [3;5] 5$ :

При $8−2√11 a= ---5--,a =3,a= 5$ решение одно,

при прочих найденных решений два.

Ошибка.
Попробуйте повторить позже

Задача 4#39871

Высота, проведённая к гипотенузе прямоугольного треугольника, делит гипотенузу на два отрезка, один из которых равен $16$ . Найдите длину второго отрезка, если радиус вписанной в этот треугольник окружности равен $5.$

Источники: ПВГ-2020, 10 класс

Подсказки к задаче

Подсказка 1

Пусть BH --- заданная в условии высота треугольника ABC из прямого угла. Давайте вспомним, что мы можем сказать про высоту к гипотенузе и длины отрезков, на которые она разбивает гипотенузу. Пусть СН=t^2, чему тогда равен отрезок ВН?

Подсказка 2

Посчитайте площадь треугольника двумя способами. Посмотрите внимательно на то, какими данными из условия мы еще не воспользовались и выберите нужные способы!

Подсказка 3

Да, первый способ – через высоту, а второй – через радиус вписанной окружности. Придумайте, как выразить полупериметр так, чтобы в нем была только сторона АС и радиус вписанной окружности!

Подсказка 4

Находим t и считаем ответ!)

Показать ответ и решение

$PIC$

Пусть это $△ABC, ∠B =90∘$ , $BH$ — высота и $AH = 16$ , второй отрезок $CH = t2$ . Тогда высота к гипотенузе $√------- BH = AH ⋅CH = 4t$ .

С одной стороны,

2 SABC = BH-⋅AC-= 4t⋅(16+t-). 2 2

С другой стороны, используя равенство $AB +BC = AC +2r$

S = PABC-⋅r= r⋅(2r+2AC-)= 5(t2+ 21). ABC 2 2

Тогда для $t$ получим кубическое уравнение

3 2 2 2t − 5t + 32t− 105 =(t− 3)(2t + t+35)= 0

Поскольку вторая скобка не имеет корней, то $t= 3 =⇒ CH =t2 = 9$ .

Ответ:

$9$

Ошибка.
Попробуйте повторить позже

Задача 5#45588

Серединный перпендикуляр к биссектрисе $AD$ треугольника $ABC$ пересекает прямую $BC$ в точке $E$ . Найдите $BC$ , если $AB :AC = 3:2$ и $CE =3$ .

Источники: ПВГ-2020

Подсказки к задаче

Подсказка 1

Подумаем сначала над тем, как хорошо бы переформулировать условие с серединным перпендикуляром. Что он нам даёт?

Подсказка 2

Верно, если у нас серединный перпендикуляр пересекает прямую в точке Е, то получается равнобедренный треугольник AED. Теперь осталось до конца воспользоваться его преимуществами. У нас есть равенство углов у равнобедренного треугольника и биссектриса. Попробуйте из этого понять что-то про угол САЕ.

Подсказка 3

Ага, видим, что углы CAE и В равны между собой. Значит, у нас есть два подобных треугольника по двум углам. Но нам неизвестна только сторона AE=AD. Вспомним, что мы ещё не пользовались свойством биссектрисы, и потом запишем соотношение для сторон из подобия.

Показать ответ и решение

$PIC$

В силу свойства биссектрисы $BD =3x,CD =2x$ . Далее заметим, что $∠EDA =∠B + ∠BAD = ∠EAD = ∠CAD + ∠EAC =⇒ ∠EAC = ∠B$ (помним, что $△AED$ равнобедренный). Отсюда $△ECA ∼ △EAB$ , то есть

EC-= EA- ⇐⇒ --3--= 3+-2x ⇐⇒ 4x2− 3x= 0 =⇒ x= 3 =⇒ BC = 15 AE EB 3+ 2x 3+ 5x 4 4

Ответ:

$15 4$

Ошибка.
Попробуйте повторить позже

Задача 6#46085

Точка $O$ является центром окружности, касающейся двух сторон треугольника $ABC$ , и лежит на стороне $BC$ . Найдите радиус окружности, описанной около треугольника $ABC$ , если $3 OB = 2,OC =2,AC = 3$ .

Источники: ПВГ-2020

Подсказки к задаче

Подсказка 1

Что за окружность такая с центром О, которая касается двух сторон угла BAC? Можем ли мы сказать, где лежит точка О?

Подсказка 2

Центр вписанной в угол окружности всегда лежит на его биссектрисе! А какое хорошее свойство есть у биссектрисы?

Подсказка 3

Она делит сторону BC точкой О в отношении, равном отношению прилежащих сторон. Теперь мы легко находим длину AB! Как по трём сторонам треугольника ABC найти радиус описанной около него окружности?

Подсказка 4

Например, радиус описанной окружности можно найти по теореме синусов! Для этого только нужен угол, который находится по трём сторонам из теоремы косинусов.

Показать ответ и решение

$PIC$

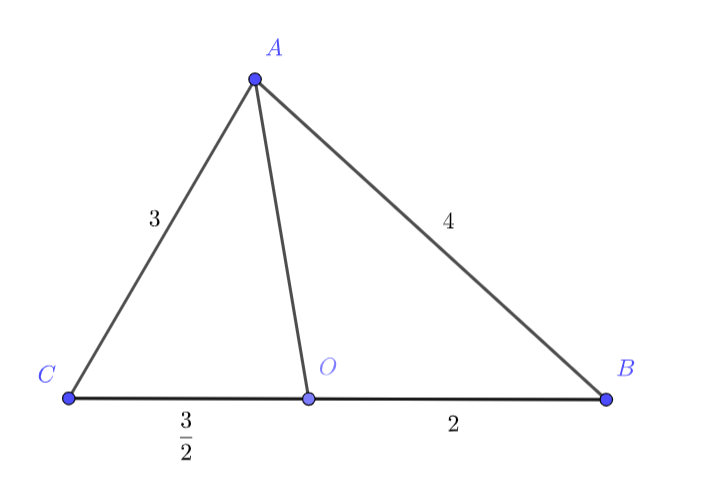
Центр $O$ вписанной в угол $ABC$ окружности лежит на биссектрисе угла $A$ . Отсюда по свойству биссектрисы $AB = BCOO-⋅AC =4$ . Мы знаем все стороны треугольника, потому можем использовать теорему косинусов для $∠A =α$

√-- 49 =32+ 42− 2 ⋅3 ⋅4 cosα =⇒ cosα = 17- =⇒ sinα = 7-15 4 32 32

Откуда $R= -BC- = √8- 2sinα 15$ .

Ответ:

$√8-- 15$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#48745

Что больше: число $3∘5√13-+18− 3∘5-√13−-18-$ или наибольший корень уравнения $x2+$ $2020x− 6069 =0$ ?

Источники: ПВГ-2020

Подсказки к задаче

Подсказка 1

Мы можем просто найти второе число! Например, по теореме Виета можно найти наибольший корень этого квадратного уравнения.

Подсказка 2

Давайте обозначим первый страшный корень за а, а второй за б. Тогда заметим, что мы можем найти аб и а³-б³! А нам как раз надо найти а-б, а мы можем попробовать найти (а-б)³!

Подсказка 3

Если обозначить а-б за х, то мы можем получить кубическое уравнение, которое у вас получится решить и сравнить два числа!

Показать ответ и решение

Наибольший корень уравнения $x2+ 2020x− 6069= 0$ равен $3$ ( $− 2023+3 =− 2020,−2023⋅3= −6069 =⇒$ по обратной теореме Виета числа $3$ и $− 2023$ являются корнями уравнения $2 x +2020x − 6069= 0).$

Обозначим $∘3-√------ 3∘ -√------ a = 5 13+ 18,b= 5 13− 18.$

Отметим, что $3 3 3∘--√--2----2 3√------- a − b = 18− (−18)=36,a⋅b= (5 13) − 18 = 325− 324 =1.$ Тогда имеем:

(a− b)3 = a3− 3a2b+ 3ab2− b3 = (a3− b3)− 3ab(a− b)=36− 3(a − b)

Получается, что число $a− b$ является одним из корней уравнения

3 t = 36− 3t

которое равносильно

t3− 3t2+ 3t2− 9t+12t− 36 =0 ⇐ ⇒ (t− 3)(t2+ 3t+12)= 0

Так как $t2+3t+ 12= 0$ не имеет действительных корней, то единственным корнем уравнения является $t= 3.$

В итоге $a− b=3.$

Ответ:

ничего, эти числа равны

Ошибка.
Попробуйте повторить позже

Задача 8#78980

Решите систему

(| √x2-− 2x+-4⋅log (4 − y)= x { ∘y2-−-2y-+4⋅log2(4− z)= y |( √ 2-------- 2 z − 2z+ 4⋅log2(4− x)= z

Источники: ПВГ - 2020, 11.4 (см. pvg.mk.ru)

Подсказки к задаче

Подсказка 1

Что сразу видно на счет этой системы? Что она симметрична, а также что в каждом уравнении используется только 2 переменных. То есть мы можем ввести функции f и g так, чтобы у нас получилось равенство вида g(y) = f(x), g(z) = f(y), g(x) = f(z). Зачем нам так делать? Потому что мы можем эти функции исследовать и что-то понять про них.

Подсказка 2

Возьмем f(x) = x/sqrt(x^2 - 2x + 4). g(x) = log_2(4 - t). Ого, но ведь производная f на всей области определения больше нуля! Это дает нам возможность перехода вида f(a) > f(b) <=> a > b. Аналогично можно сказать и про g, только на счет убывания. Тогда, идейно, остается найти какое-то одно решение системы и доказать, что других нет.

Подсказка 3

Подходит решение (2, 2, 2). Теперь можно предположить, что наша система имеет другое решение, то есть хотя бы 1 переменная не равна 2. Пусть тогда x < 2. Если у нас есть это неравенство и неравенство из 2-ой подсказки, то как нам прийти к противоречию (показать, что тогда х > 2)?

Показать ответ и решение

Введём в рассмотрение функции

----t---- f(t)= √t2−-2t+4-и g(t) =log2(4− t)

Под радикалами находятся заведомо положительные выражения $x2− 2x +4= (x− 1)2+ 3,$ поэтому на них можно поделить, а система примет такой вид:

( |{ g(y)= f(x) |( g(z)= f(y) g(x)= f(z)

Область определения системы задаётся тем, что каждая переменная меньше 4.

На этой области определения функция $g(t)$ монотонно убывает, а функция $f(t)$ имеет положительную производную:

f′(t)= -2-4−-t--3 >0 при t< 4, (t − 2t+4)2

поэтому является монотонно возрастающей.

Далее существует два способа решения:

Первое решение.

Заметим, что $x= y = z = 2$ является решением системы. Покажем, что других решений нет.

Действительно, пусть $x <2.$ Но тогда

log2(4− y)= f(x)< f(2)= 1 =⇒ 4− y < 2 =⇒ y > 2 =⇒

log (4 − z)= f(y)> f(2)= 1 =⇒ 4− z >2 =⇒ z < 2 =⇒ 2

log2(4 − x)= f(z)< f(2) =1 =⇒ 4− x< 2 =⇒ x >2

сразу же получаем противоречие. Ясно, что случай $2< x< 4$ рассматривается полностью аналогично.

Второе решение.

В силу обратимости функции $g$ получается явно выразить любую из переменных, причём выражаются они одинаково в силу цикличности системы:

y = 4− 2f(x) =4 − 2f(4−2f(z)) =4− 2f(4−2f(4−2f(y)))

y = h(h(h(y)))),

где функция $h(u)= 4− 2f(u)$ монотонно убывает по правилам монотонности сложной функции.

Тогда в правой части уравнения функция $s(y)=h(h(h(y)))$ монотонно убывает, а в левой части уравнения функция $t(y)= y$ , очевидно, монотонно возрастает. Поэтому равенство $t(y)= h(y)$ возможно не более, чем в одной точке. И при $y = 2$ оно как раз достигается. Всё проделанное справедливо и для оставшихся двух переменных.

Ответ:

$(2;2;2)$

Ошибка.
Попробуйте повторить позже

Задача 9#90896

Велотрек имеет форму окружности. Из его диаметрально противоположных точек одновременно стартуют два велосипедиста, которые двигаются против часовой стрелки с постоянными скоростями. Сколько полных кругов проедет каждый велосипедист до того момента как они поравняются первый раз после старта, если отношение их скоростей равно $32 31$ .

Источники: ПВГ - 2020, 11.2 (pvg.mk.ru))

Подсказки к задаче

Подсказка 1

Давайте обозначим скорость более медленного за v, а длину за S. С какой скоростью они приближаются друг к другу?

Подсказка 2

Они приближаются друг к другу со скоростью 32v/21 - v. А каким расстояние между ними было изначально?

Подсказка 3

Изначально расстояние между ними было S/2, а должно стать нулём.

Показать ответ и решение

Пусть $S$ — длина круга, а $v$ — скорость более медленного. Тогда они встретятся через $-S2---= 31S- 3231v−v 2v$ времени. За это время медленный проедет 15 с половиной кругов, а быстрый 16.

Ответ: медленный проедет 15 с половиной кругов, а быстрый 16

Ошибка.
Попробуйте повторить позже

Задача 10#100192

Найдите все значения параметра $a$ , при каждом из которых неравенство

-----------1---------- √- √x2-+2x-+5+ √x2+-6x+-18-≤ a

выполняется при всех значениях $x.$

Источники: ПВГ - 2020, 11.5 (pvg.mk.ru))

Подсказки к задаче

Подсказка 1

Так как нам нужно, чтобы неравенство выполнялось при всех x, то какое крайнее значение левой части стоит рассмотреть? При каком знаменателе оно достигается?

Подсказка 2

Рассмотрите наибольшее значение левой части. Для этого нужно минимизировать знаменатель;) Можно пробовать его преобразовать так, чтобы найти геометрическую интерпретацию знаменателю.

Подсказка 3

Представьте подкоренные выражения в виде суммы квадратов. Каков геометрический смысл суммы корней?

Подсказка 4

Это сумма расстояний от двух точек до некоторой одной! А когда она достигает наименьшего значения?

Подсказка 5

Когда точки лежат на одной прямой ;)

Показать ответ и решение

Так как знаменатель функции

-----------1---------- f(x)= √x2-+2x+-5+ √x2+-6x+18-

равен

∘ ---------- ∘ ---------- g(x)= (x +1)2+22+ (x +3)2+32

и всегда положителен, то наибольшему значению функции соответствует наименьшее значение знаменателя. При этом функцию $∘ ---------- ∘ ---------- g(x)= (x+ 1)2+ 22+ (x+3)2+ 32$ можно трактовать как сумму двух расстояний: от точки $(x;0)$ до точки $A(−1;2)$ и от точки $(x;0)$ до точки $B(−3;− 3)$ . Мы специально выбрали точки так, что они лежат по разные стороны от оси абсцисс, тогда наименьшее значение суммы достигается в точке пересечения прямой $AB$ и оси абсцисс. Это будет точка $x= − 95$ , но вычислять ее нет необходимости, так как наименьшее значение функции просто равно длине отрезка

∘-------------- AB = (3− 1)2+ (3 +2)2 = √29.

Поэтому наибольшим значением функции $f(x)= g1(x)$ является $√129$ . Значит,

√a≥ √1- 29

a≥ -1 29

Ответ:

$( 1-;+∞) 29$

Ошибка.
Попробуйте повторить позже

Задача 11#100193

Андрей выбирает случайным образом целое число $a$ из отрезка $[−5;6]$ и после этого решает уравнение

3 2 3x − (3a− 4)x − (2a− 3)x +a+ 2= 0.

Найдите вероятность того, что Андрей получит три различных корня, из которых как минимум два будут целыми, если точно известно, что при вычислениях он не ошибается.

Источники: ПВГ - 2020, 11.4 (pvg.mk.ru))

Подсказки к задаче

Подсказка 1

По условию становится понятно, что нам всё же придется искать корни кубического уравнения. Давайте тогда попробуем для начала найти хотя бы один из них. Попробуем разложить на множители выражение из условия.

Подсказка 2

Здорово, теперь мы знаем, что -1 — точно корень, вне зависимости от a. Получается, что нам хотелось бы добиться, чтобы у оставнегося квадратного уравнения был как миниму 1 целый корень, отличный от -1.

Подсказка 3

После деления выражения на (x+1) выразите a через выражения с x. Так как мы хотим добиться целого x, имеет смысл выделить целую часть.

Подсказка 4

Вспомните, что a тоже целое! Каким тогда будет x, если он присутствует в дроби 8/(3x-1)?

Подсказка 5

Если х целое, оно будет обязательно делителем 8. Отсюда несложно разобрать случаи a.

Показать ответ и решение

Так как

3 2 ( 2 ) 3x − (3a− 4)x − (2a− 3)x+ a+ 2= (x+ 1) 3x − (3a − 1)x+ a+2 ,

то $x= −1$ будет корнем при всех $a$ . Решим в целых числах уравнение

2 3x − (3a− 1)x+ a+ 2= 0

Его удобно записать в виде $a(3x− 1)=3x2+ x+ 2$ или

3x2+ x+ 2 x(3x− 1)+ 23(3x− 1)+ 83 2 8 a = -3x−-1--= -------3x-− 1------ =x + 3 + 3(3x−-1)

Поэтому $3a =3x+ 2+ 38x−-1$ , и значит, $3x− 1$ равно одному из чисел $±1,±2,±4,±8$ . В итоге получаем целые решения: $x =1$ , если $a =3; x =3$ , если $a= 4; x =0$ , если $a= −2; x =− 1$ если $a= −1$ .

Таким образом, при всех $a$ , кроме а равному $3,4,− 2$ и -1 , исходное уравнение имеет один целый корень $x =− 1$ а других целых корней не имеет.

При $a= 3$ уравнение имеет целые корни $x =− 1,x =1$ и корень $x= 53$ .

При $a= 4$ уравнение имеет целые корни $x =− 1,x =3$ и корень $x= 23$ .

При $a= −2$ уравнение имеет целые корни $x= −1,x =0$ и корень $x= − 73$ .

При $a= −1$ уравнение имеет два корня: $x= −1$ и $x =− 13$ .

Поэтому три различных корня, из которых два будут целыми, получаются в 3 случаях из 12. Вероятность равна $312 = 14$ .

Ответ:

$1 4$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#102398

В алфавите жителей сказочной планеты АБ2020 всего две буквы: буква А и буква Б. Все слова начинаются на букву А и заканчиваются тоже на букву А. В любом слове буква А не может соседствовать с другой буквой А. Также не может идти подряд больше, чем $2$ буквы Б. Например, слова АББА, АБАБАБА, АББАБАББА являются допустимыми, а слова АББАБ, АБААБА, АБАБББА — нет. Сколько $20$ -буквенных слов в словаре этой планеты?

Источники: ПВГ - 2020, 11.5 (pvg.mk.ru))

Подсказки к задаче

Подсказка 1

Ого, нам нужно сделать какие-то выводы о словах, в которых аж 20 букв.. Попробовать выписать их все — не вариант, ведь их может быть слишком много. Давайте тогда в целом посмотрим на словарь инопланетян. Сколько там совсем маленьких слов, состоящих из одной, двух, трёх, четырёх букв?

Подсказка 2

Было бы здорово найти какую-нибудь формулу для количества слов, состоящих из n букв. Мы знаем, чему равно это количество для маленьких n, поэтому можем попробовать найти рекуррентное соотношение. Что мы можем сказать про слово из n букв?

Подсказка 3

То, что в нём соблюдаются все условия на то, чтобы строка была словом, а значит, оно заканчивается на букву А. Тогда предпоследняя буква — это Б. А что слоит перед Б? Рассмотрите несколько случаев и поймите, как устроено слово из n букв.

Подсказка 4

Получается, слово из n букв — это либо слово из n-2 букв, к которому приписали БА, либо слово из n-3 букв, к которому приписали ББА. Теперь не трудно написать рекуррентную формулу и найти искомое количество:)

Показать ответ и решение

Пусть $W i$ — это количество слов инопланетят, состоящих из $i$ букв.

Заметим, что единственное однобуквенное слово — это слово А. Двухбуквенных слов вообще нет, так как первая и последняя, то есть первая и вторая буквы — это А, но тогда две буквы А стоят рядом, что противоречит определению инопланетного слова. Трёхбуквенное слово тоже только одно — АБА. И четырёхбуквенное слово единственно — АББА. Таким образом,

W1 =1,W2 =0,W3 =1,W4 =1

Рассмотрим теперь какое-нибудь слово $ω$ длины $n,$ где $n >4.$ Его последняя буква — это точно буква А, так как каждое слово начинается и заканчивается буквой А. Предпоследняя буква — это Б, так как две буквы А не могут идти подряд. Есть два варианта, какой может быть буква перед Б, то есть предпредпоследняя буква слова $ω$ :

1) Это буква А. Тогда слово $ω$ имеет вид А...АБА. Рассмотрим строку из первых $n− 2$ букв этого слова. Она начинается и заканчивается на А, а так же в ней нет двух букв А подряд или трёх букв Б подряд, так как иначе $ω$ не было бы словом. А значит эта строка сама является словом.

2) Это буква Б. Тогда перед этой буквой Б стоит буква А, там как три буквы Б не могут идти подряд, и слово $ω$ имеет вид А...АББА. Аналогично случаю 1, строка, образованная первыми $n− 3$ буквами $ω$ будет являться словом.

Получается, что слово $ω$ могло быть получено либо приписыванием строки БА в конец какого-нибудь слова из $n − 2$ букв, либо приписыванием строки ББА в конец какого-нибудь слова из $n− 3$ букв. При этом, приписав в конец каждого из $Wn−2$ слов длины $n− 2$ строку БА, мы получим $Wn−2$ различных слов длины $n.$ Аналогично, приписав в конец каждого из $Wn −3$ слов длины $n − 3$ строку ББА, мы получим $Wn −3$ различных слов длины $n.$ Отсюда,

Wn = Wn−2+ Wn−3

Пользуясь этой формулой, найдем $Wi$ для $i= 5,...,20.$


$W1$	$W2$	$W3$	$W4$	$W5$	$W6$	$W7$	$W8$	$W9$	$W10$

$1$	$0$	$1$	$1$	$1$	$2$	$2$	$3$	$4$	$5$

Итак, в словаре сказочной планеты 86 20-буквенных слов.

Ответ:

Ошибка.
Попробуйте повторить позже

Задача 13#120842

Иван Семёнович каждый день выезжает в одно и то же время, едет на работу с одной и той же скоростью и приезжает ровно в $9:00.$ Однажды он проспал и выехал на $40$ мин. позднее обычного. Чтобы не опоздать, Иван Семёнович поехал со скоростью на $60%$ большей, чем обычно и приехал в $8:35.$ На сколько процентов он должен был увеличить обычную скорость, чтобы приехать ровно в $9 :00?$

Подсказки к задаче

Подсказка 1

Пусть он едет со скоростью v километров в минуту и тратит t минут на дорогу. Перепишите условие задачи в данных терминах.

Подсказка 2

Не забывайте, что скорость должна быть положительной. Пусть ему надо было увеличить скорость на k процентов, как ее тогда можно записать?

Показать ответ и решение

Пусть Иван Семёнович обычно едет со скоростью $v$ километров в минуту и тратит $t$ минут на дорогу. Тогда расстояние до его работы равно $vt$ километров.

В день, когда он проспал, он выехал из дома на $40$ минут позже, а приехал на место на $25$ минут раньше, таким образом, время его пути уменьшилось на $65$ минут и стало равно $t− 65$ минут. А его скорость в тот день была равна $1,6v.$ Тогда расстояние до его работы равно $1,6v(t− 65)$ километров. Получается,

vt= 1,6v(t− 65)

v(t− 1,6t+ 1,6⋅65)= 0

Итак, $v ⁄=0,$ так как скорость положительна, поэтому $t= 520 3$ минут.

Пусть ему нужно было увеличить свою обычную скорость на $k$ процентов, чтобы приехать ровно в $9:00.$ В этом случае время его пути будет равно $t− 40$ минут, а скорость — $100-+k- 100 ⋅v$ километров в минуту. Отсюда: