Тема Турнир городов - задания по годам

Турнир городов 2016

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела турнир городов - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#72106

Существуют ли $2016$ целых чисел, сумма и произведение которых равны $2016?$

Источники: Турнир городов - 2016, весенний тур, базовый вариант, 11.2

Подсказки к задаче

Подсказка 1

Попробуем подобрать пример, исходя из того, что произведение равно 2016.

Подсказка 2

Нам ведь нужно, чтобы и сумма равнялась 2016.

Подсказка 3

А если взять числа 2 и 1008?

Показать ответ и решение

Попробуем подобрать пример, исходя из того, что произведение равно $2016.$ Пусть первое число равно $2,$ а второе — $1008.$ Тогда остальные числа могут быть только $± 1$ (притом количество $− 1$ чётное). Сумма $1008$ и $2$ равна $1010,$ значит сумма единиц должна быть $1006.$ Если взять $504$ минус единицы и $1510$ единиц, то мы получим требуемое.

Ответ:

Да, существуют

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#73703

Дана бесконечно возрастающая арифметическая прогрессия. Первые её несколько членов сложили и сумму объявили первым членом новой последовательности, затем сложили следующие несколько членов исходной прогрессии и сумму объявили вторым членом новой последовательности, и так далее. Могла ли новая последовательность оказаться геометрической прогрессией?

Подсказки к задаче

Подсказка

Попробуем разбить натуральные числа по степеням какого-то небольшого натурального числа. Как тогда будут выглядеть суммы подряд идущих чисел?

Показать ответ и решение

Пример 1

1 n 1 n+1 n 1,2 +3+ 4,5+...+13,...,2(3 + 1)+...+ 2(3 − 1),...= 1,9,81,...,9

Пример 2

3,5+ 7,...,(2n+ 1)+...+ (2n+1 − 1),...=3,12,...,3⋅4n−1,...

Ответ:

Могла

Ошибка.
Попробуйте повторить позже

Задача 3#96567

В квадрате $10× 10$ все клетки левого верхнего квадрата $5× 5$ закрашены чёрным цветом, а остальные клетки — белым. На какое наибольшее количество многоугольников можно разрезать (по границам клеток) этот квадрат так, чтобы в каждом многоугольнике чёрных клеток было в три раза меньше, чем белых? (Многоугольники не обязаны быть равными или даже равновеликими.)

Источники: Турнир городов - 2016, весенний тур, базовый вариант, 11.3

Подсказки к задаче

Подсказка 1

Видим задачку типа «оценка + пример», давайте попробуем как-то получить оценку. Наверняка у нас есть какой-то объект, который должен быть в каждом многоугольнике, но количество которых на нашей картинке ограничено. Что это может быть?

Подсказка 2

Так как в каждом многоугольнике есть белая и чёрная клетки, должна быть хотя бы одна чёрная клетка, граничащая с белой! А таких клеток у нас не так уж и много)

Подсказка 3

У нас есть всего девять таких клеток, значит, количество многоугольников точно не больше девяти! Остается придумать пример разбиения на 9 многоугольников)

Показать ответ и решение

В каждом многоугольнике разбиения должны быть клетки обоих цветов. Значит, в нём должна быть чёрная клетка, граничащая с белой. Но таких клеток всего 9.

Пример разрезания на 9 многоугольников (для светлой темы):

$PIC$

Здесь 8 многоугольников с 1 чёрной клеткой и 3 белыми, оставшийся многоугольник содержит 17 чёрных клеток и 51 белую.

Ответ: 9

Ошибка.
Попробуйте повторить позже

Задача 4#96651

В стране $64$ города, некоторые пары из них соединены дорогой, но нам неизвестно, какие именно. Мы можем выбрать любую пару городов и получить ответ на вопрос “есть ли дорога между ними?”. Мы хотим узнать, можно ли в этой стране добраться от любого города до любого другого, двигаясь по дорогам. Докажите, что не существует алгоритма, позволяющего сделать это менее чем за $2016$ вопросов.

Подсказки к задаче

Подсказка 1

Нужно показать, что для любой последовательности наших запросов существует граф, который после неë может быть как связным, так и несвязным.

Подсказка 2

Если бы перед последним запросом граф был деревом, то после последнего запроса он могу бы быть как связным, так и несвязным. Подумайте, как к последовательности запросов подобрать граф, который станет деревом.

Показать доказательство

Переформулируем задачу. Дан полный граф на $64$ вершинах с белыми рёбрами (их всего $2016).$ Играют двое. Петя указывает белое ребро, а Вася удаляет его или делает чёрным. Перед последним ходом Петя предсказывает, какой в итоге получится граф — связный или нет. Докажем, что Вася может опровергнуть любое предсказание Пети. Всё время рассматриваем граф всех вершин и оставшихся белых и чёрных рёбер. Если указанное Петей ребро содержится в каком-то цикле, то Вася удаляет его, иначе — делает чёрным. При этом связность графа сохраняется, а чёрные рёбра в циклы не входят. Перед последним ходом остаётся лишь одно белое ребро. Значит, циклов не осталось, и граф — дерево. Поэтому Вася может как удалить это ребро, нарушив связность, так и сохранить вместе со связностью.

Ошибка.
Попробуйте повторить позже

Задача 5#104685

На катетах $AC$ и $BC$ прямоугольного треугольника $ABC$ отметили точки $K$ и $L$ соответственно, а на гипотенузе $AB$ — точку $M$ так, что $AK = BL =a,$ $KM =LM =b$ и угол $KML$ прямой. Докажите, что $a= b.$

Подсказки к задаче

Подсказка 1

Попробуйте понять, какие фигуры у нас есть на картинке.

Подсказка 2

Заметим, что четырехугольник MKCL — вписанный.

Подсказка 3

А чему будет равна сумма ∠AKM и ∠BML?

Подсказка 4

Попробуйте из имеющихся фигур собрать одну, обладающую "приятным" свойством.

Показать доказательство

Четырёхугольник $MKCL$ вписанный, а значит,

∘ ∠AKM +∠MLB = ∠CLM + ∠CKM = 180

Также из условия следует, что

∠AKM + ∠BML =180∘− ∠KML = 90∘

$PIC$

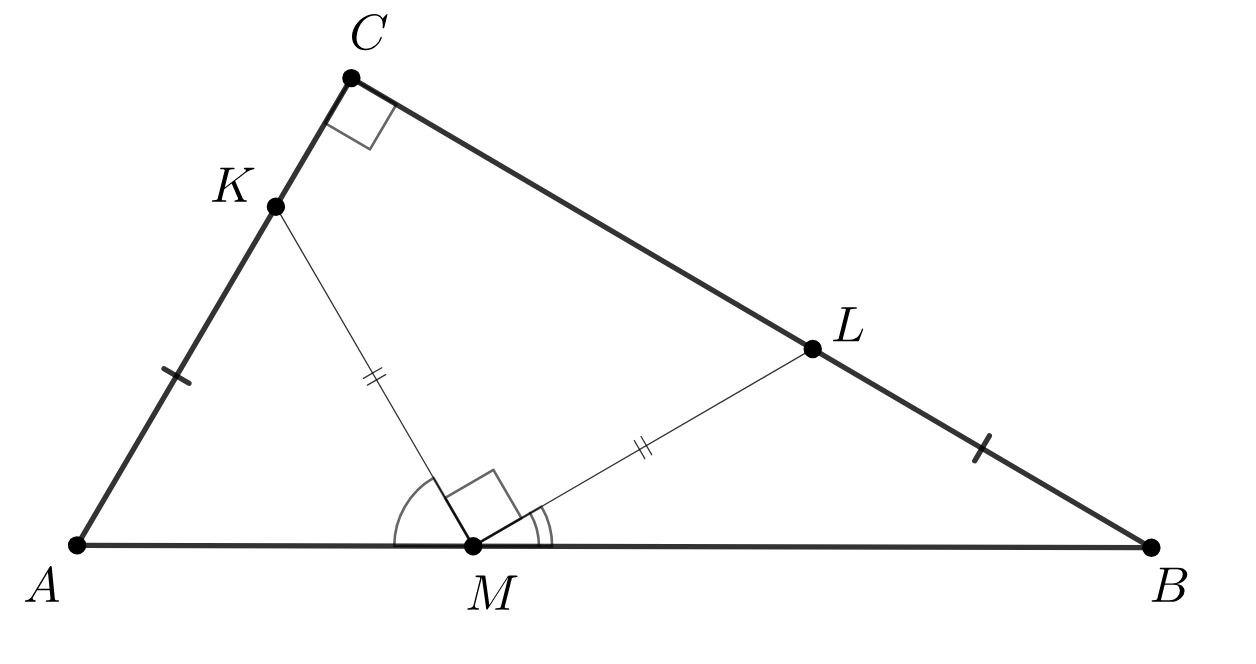
Заметим, что если совместить треугольники $AKM$ и $BML$ по стороне, равной $b,$ точкой $K$ к точке $L,$ то тогда получится прямоугольный треугольник с гипотенузой $2a$ и медианой $b$ , проведённой к ней. Отсюда получаем $a= b.$

$PIC$