Иннополис 2020
Ошибка.
Попробуйте повторить позже
Рассмотрим уравнение 
на множестве положительных действительных чисел. Вам требуется явно указать для каждого
вещественного значения 
число таких различных вещественных чисел 
что 
(Пример явного описания: для 
существует единственное число 
такое, что 
Источники:
Подсказка 1
Случай x = 1 уже описан в формулировке задачи. Будем далее полагать, что x ≠ 1 и y ≠ 1. Какие методы решения подобных уравнений Вам знакомы?
Подсказка 2
У нас показательное уравнение. Попробуйте взять логарифм от обеих частей.
Подсказка 3
Мы получим x ⋅ ln(y) = y ⋅ ln(x). И слева, и справа x и y. Давайте перегруппируем множители.
Подсказка 4
Разделим обе части на xy, получим ln(x)/x = ln(y)/y. Видите ли Вы здесь какую-нибудь функцию?
Подсказка 5
Вообще говоря, из нашего уравнения следует, что x/ln(x) = y/ln(y). Рассмотрите функцию f(z) = z/ln(z). Попробуйте построить её график.
Подсказка 6
Чтобы определить области возрастания и убывания f(z), возьмем её производную. Получится (ln(z) - 1) / ln²(z).
Подсказка 7
На интервале (0; 1) функция f убывает от 0 до -∞, на интервале (1; e) f тоже убывает, достигая локального минимума f(e) = e. Потом на интервале (e; +∞) возрастает от e до +∞. Теперь возьмите x > 0 и попробуйте подвести итоги.
Подсказка 8
Например, если 0 < x < 1, то (x / ln(x)) < 0 и функция непрерывно убывает, следовательно (чтобы в этом убедиться, можно нарисовать график), будет единственное подходящее нам вещественное y. Аналогично с остальными промежутками.
Случай 
уже описан в формулировке задачи, поэтому в дальнейшем мы можем предполагать, что 
и 
Возьмем натуральный логарифм от обеих частей исходного уравнения и получим следующее уравнение
Так как 
и 
то это уравнение равносильно новому уравнению
Проанализируем функцию 
и построим ее график. Так как
то на интервале 
функция 
убывает от 
до 
на интервале 
функция 
тоже убывает, достигая локального
минимума 
при 
а потом на интервале 
возрастает от 
до 
Подведём итоги. Пусть 
— произвольное положительное действительное число. Имеем:
- если
то 
и, следовательно, (см. график) существует только единственное подходящее нам вещественное
число 
- если
то, как это уже было сказано, существует только единственное подходящее вещественное число 
- если
или если 
то 
и, следовательно, (см. график) существуют два подходящих вещественных
числа 
- если
то 
и, следовательно, (см. график) существует единственное подходящее вещественное число 
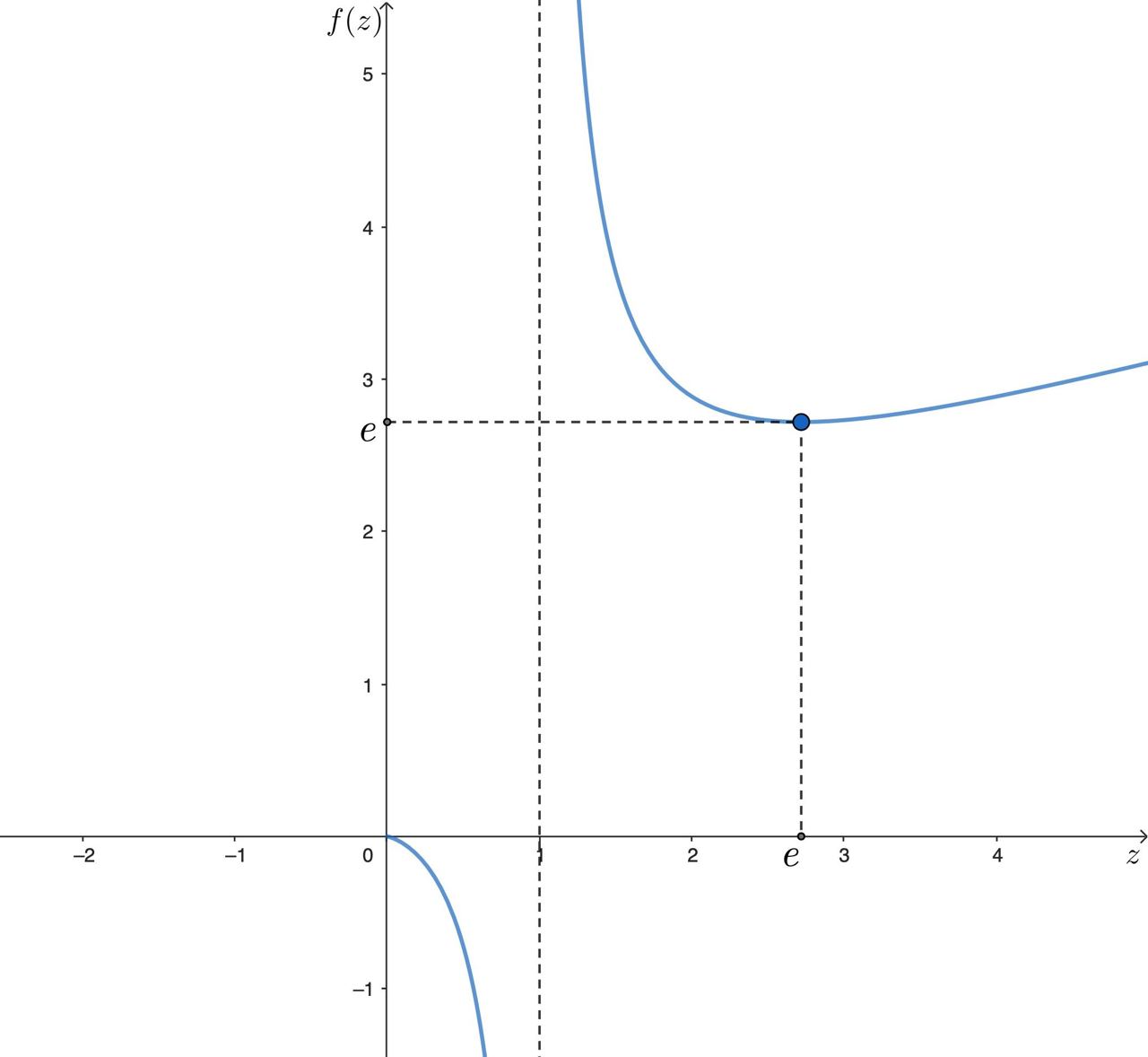
При ![x∈ (0;1]∪e](/api/latex-service/v1/GetSession/257617/index-e45381b0c0c7daa61ec0d873cd8ab766.svg)
— одно решение; при 
— два решения
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
