Иннополис 2020
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Рассмотрим уравнение на множестве положительных действительных чисел. Вам требуется явно указать для каждого
вещественного значения
число таких различных вещественных чисел
что
(Пример явного описания: для
существует единственное число
такое, что
Источники:
Подсказка 1
Случай x = 1 уже описан в формулировке задачи. Будем далее полагать, что x ≠ 1 и y ≠ 1. Какие методы решения подобных уравнений Вам знакомы?
Подсказка 2
У нас показательное уравнение. Попробуйте взять логарифм от обеих частей.
Подсказка 3
Мы получим x ⋅ ln(y) = y ⋅ ln(x). И слева, и справа x и y. Давайте перегруппируем множители.
Подсказка 4
Разделим обе части на xy, получим ln(x)/x = ln(y)/y. Видите ли Вы здесь какую-нибудь функцию?
Подсказка 5
Вообще говоря, из нашего уравнения следует, что x/ln(x) = y/ln(y). Рассмотрите функцию f(z) = z/ln(z). Попробуйте построить её график.
Подсказка 6
Чтобы определить области возрастания и убывания f(z), возьмем её производную. Получится (ln(z) - 1) / ln²(z).
Подсказка 7
На интервале (0; 1) функция f убывает от 0 до -∞, на интервале (1; e) f тоже убывает, достигая локального минимума f(e) = e. Потом на интервале (e; +∞) возрастает от e до +∞. Теперь возьмите x > 0 и попробуйте подвести итоги.
Подсказка 8
Например, если 0 < x < 1, то (x / ln(x)) < 0 и функция непрерывно убывает, следовательно (чтобы в этом убедиться, можно нарисовать график), будет единственное подходящее нам вещественное y. Аналогично с остальными промежутками.
Случай уже описан в формулировке задачи, поэтому в дальнейшем мы можем предполагать, что
и
Возьмем натуральный логарифм от обеих частей исходного уравнения и получим следующее уравнение
Так как и
то это уравнение равносильно новому уравнению
Проанализируем функцию и построим ее график. Так как
то на интервале функция
убывает от
до
на интервале
функция
тоже убывает, достигая локального
минимума
при
а потом на интервале
возрастает от
до
Подведём итоги. Пусть — произвольное положительное действительное число. Имеем:
- если
то
и, следовательно, (см. график) существует только единственное подходящее нам вещественное число
- если
то, как это уже было сказано, существует только единственное подходящее вещественное число
- если
или если
то
и, следовательно, (см. график) существуют два подходящих вещественных числа
- если
то
и, следовательно, (см. график) существует единственное подходящее вещественное число
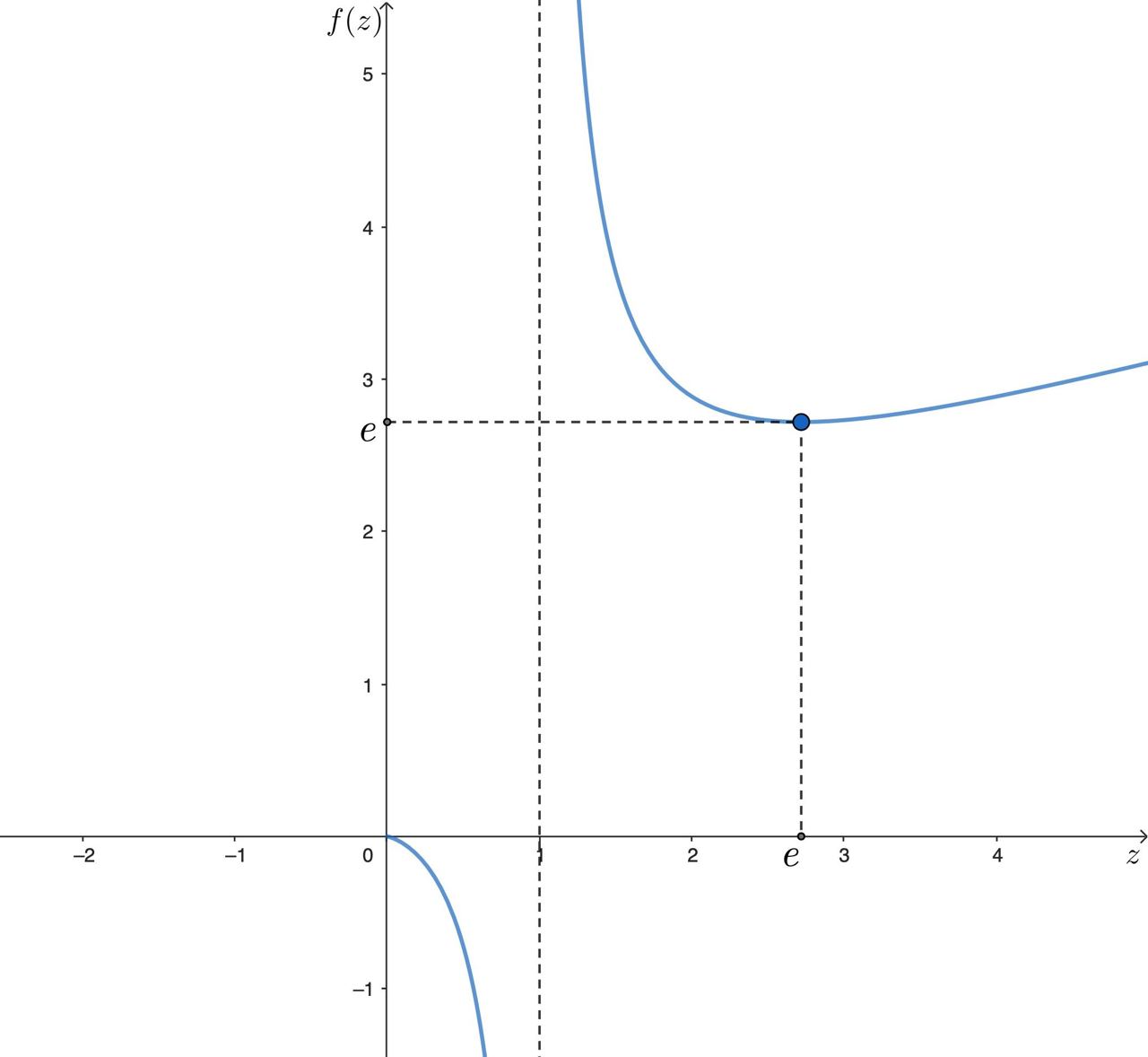
При — одно решение; при
— два решения
Ошибка.
Попробуйте повторить позже
Найдите и докажите явное выражение (в терминах известных операций на целых числах) для функции вычисляющей пару
чисел
и определенной следующим образом для любых целых значений
и любых целых значений
Источники:
Подсказка 1
Давайте для начала попробуем вычислить некоторые значения функции g.
Подсказка 2
Возьмем m, близкое к 100, например, 98.
Подсказка 3
g(98, n) = (p₁ - 1, q₁). Заметьте, что (p₁, q₁) = g(g(99, n)). Продолжите эти вычисления, пока не сможете выразить g(98, n) через числа и, возможно, n.
Подсказка 4
У нас должны получиться явные выражения для g(98, n), g(99, n) и (p₁, q₁). Это будет в следующей подсказке, но постарайтесь дойти самостоятельно.
Подсказка 5
g(98, n) = (98, (n + 4)); g(99, n) = (99, (n + 2)); g(100, n) = (100, (n + 1)). Есть ли тут какая-то зависимость?
Подсказка 6
Возникает предположение, что g(m, n) = (m, (2¹⁰⁰⁻ᵐ + n)). Попробуйте это доказать.
Подсказка 7
Перепишем формулу следующим образом: g((100 - m), n) = ((100 - m), (2ᵐ + n)). Докажем это индукцией по m ≥ 0.
Подсказка 8
При m = 0 все получится, это база индукции. Теперь надо доказать для (m + 1). Подставим его в формулу.
Подсказка 9
По предположению индукции, g((100 - m), n) = ((100 - m), (2ᵐ + n)) (при k = m). Раскройте выражения, как в самом начале, и получите требуемое.
Докажем индукцией по что для любого целого положительного
выполняется
База индукции :
По формуле, которую мы доказываем, при :
База верна.
Индукционная предположение: Пусть для всех и для любого
верно
Шаг индукции (для ):
Нам нужно доказать, что
- 1.
-
где
(по определению функции
если первый аргумент не
- 2.
-
по предположению индукции (для
- 3.
-
согласно пункту
- 4.
-
по предположению индукции, применяя его к
где
и
- 5.
-
согласно пунктам
и
- 6.
-
согласно пунктам
и
- 7.
-
согласно пунктам
и
Что и требовалось доказать.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание. Чтобы догадаться до решения, можно было проделать этот эксперимент: вычислим «символически» значение функции
для какого-либо значения
близкого к
например, вычислим
- 1.
-
где
- 2.
-
где
- 3.
-
следует из п.
- 4.
-
следует из п.
и
- 5.
-
где
- 6.
-
следует из п.
и
- 7.
-
следует из п.
и
Из этого эксперимента видно, что
— см. определение функции (предполагая, что
и
— см. пункт
эксперимента;
— см. пункт
эксперимента.
Поэтому возникает предположение, что
Ошибка.
Попробуйте повторить позже
Найдите максимальное целое число для которого верно следующее утверждение: «Существует способ найти (определить)
единственную фальшивую монету среди
внешне одинаковых монет, взвешивая монеты на чашечных весах (без числовых делений) не
более трех раз и одновременно определить ее относительный вес (то есть легче она или тяжелее настоящих)». (Замечание:
предполагается, что все настоящие монеты имеют одинаковый вес, а фальшивая — другой вес, отличный от веса настоящих
монет).
Источники:
Подсказка 1
Сколько результатов можно получить за 3 взвешивания?
Подсказка 2
За одно взвешивание можно получить 3 результата, поэтому за 3 взвешивания получим 27. Теперь оцените n.
Подсказка 3
Количество вариантов фальшивой монеты и её относительного веса равно 2n, поэтому 2n ≤ 27 ⇒ n ≤ 13.
Подсказка 4
Будем перебирать n сверху. Пусть n = 13. Давайте предположим, что способ определить фальшивую монету существует, тогда либо приведем его, либо получим противоречие.
Подсказка 5
Заметим, что за 2 взвешивание можно получить только 9 результатов. Докажите, что в каждом взвешивании должно участвовать не менее 10 монет.
Подсказка 6
Докажите, что иначе в первом взвешивании участвует не более 8 монет.
Подсказка 7
Рассмотрите ситуации, когда в первом взвешивании участвует 10 монет, и сравните количества результатов с количествами вариантов.
Подсказка 8
Доказали, что n ≠ 13. Пусть n = 12. Попробуйте придумать алгоритм поиска фальшивой монеты. Сколько монет должно участвовать в первом взвешивании?
Подсказка 9
В первом взвешивании должно участвовать 8 монет, разберите ситуации, когда левая чаша тяжелее; правая чаша тяжелее; чаши уравновешены.
Сначала заметим, что за три взвешивания на чашечных весах можно получить только 27 результатов за каждое взвешивание на
чашечных весах можно получить только 3 результата — левая чашка легче правой, чашки уравновешены, правая чашка
Но
так как количество вариантов фальшивой монеты
и ее относительного веса
равно
то должно выполняться
неравенство
Следовательно,
Пусть
Докажем методом от противного, что определить фальшивую монету и одновременно её относительный вес требуемым способом невозможно. Для этого предположим противное, то есть то, что есть такой способ.
Заметим, что так как за одно взвешивание на чашечных весах можно получить только 3 результата легче правой,
чашки уравновешены, правая чашка
то за два взвешивания на чашечных весах можно получить только 9
результатов.
Теперь покажем, что в первом взвешивании должно участвовать не менее 10 монет . Действительно, в противном случае в первом
взвешивании участвует не более 8 монет
быть чётным, так как взвешивание происходит на чашечных весах, а на чашки
весов надо класть равные
Значит, если в результате первого взвешивания чашки весов уравновесятся, то фальшивая монета — одна из не менее, чем 5 монет, не
участвовавших в первом взвешивании, она может быть как легче, так и тяжелее настоящих, и, следовательно, у нас возможно не менее 10
вариантов и её
А так как число результатов, которые можно получить за два взвешивания, меньше числа вариантов, то определение фальшивой монеты и её относительного веса невозможно.
В первом взвешивании участвует не менее 10 монет — не менее 5 на каждой чаше весов. Если в результате первого взвешивания одна
чашка
чем 5
оказалась легче, а другая
не менее, чем 5
— тяжелее, то у нас возможно не
менее 10 вариантов
и ее
Вновь число результатов за 2 взвешивания будет меньше числа
вариантов.
Таким образом, предположив существование способа с помощью чашечных весов определить фальшивую монету и одновременно её относительный вес, мы пришли к заключению, что способ не существует, то есть — к противоречию с предположением.
Пусть
В описании способа определения фальшивой монеты будем использовать следующие обозначения:
- 1.
-
Монеты будем обозначать
а
—
- 2.
-
Выражения вида
для взвешивания, в котором, в данном случае, пара монет
и
помещены на левую чашку весов, а пара других монет
и
(тоже из монет и гирьки) — на правую.
- 3.
-
У взвешивания
может быть три исхода: <
левая чашка
=
чашки
и >
правая чашка
- 4.
-
означает «для такого выражения возможны следующие случаи» (и далее — случаи для =, > и <).
Теперь мы можем дать описание алгоритма, который получает 12 монет , среди которых ровно одна фальшивая имеет вес,
отличный от веса других настоящих монет равного веса, и определяет фальшивую монету и ее относительный вес за три взвешивания на
чашечных весах. В круглых скобках находятся пояснения к каждому шагу.
(сначала мы кладем на левую чашу монеты с 1 по 4, а на вторую — с 5 по 8, остальные подобные выражения читаются
аналогично)
(получили равенство, тогда фальшивая среди
, а все
— настоящие):
-
(то есть фальшивая (12)):
: фальшивая монета (12) и тяжелее;
: фальшивая монета (12) и легче;
-
(то есть фальшивая среди (9) и легче или среди (10) и (11) и тяжелее):
(возможно только если (9) фальшивая и легче): фальшивая монета (9) и легче;
(возможно только если (11) фальшивая и тяжелее): фальшивая монета (11) и тяжелее;
(возможно только если (10) фальшивая и тяжелее): фальшивая монета (10) и тяжелее;
-
(то есть фальшивая среди (9) и тяжелее или среди (10) и (11) и легче):
(возможно только если (9) фальшивая и тяжелее): фальшивая монета (9) и тяжелее;
(возможно только если (10) фальшивая и легче): фальшивая монета (10) и легче;
(возможно только если (11) фальшивая и легче): фальшивая монета (11) и легче;
(то есть фальшивая среди
и легче, или среди
и тяжелее, а все
— настоящие):
-
(то есть фальшивая среди (4) и легче, или (7) и (8) и тяжелее, а все остальные монеты — настоящие):
(возможно только если фальшивая (4) и легче): фальшивая монета (4) и легче;
(возможна только если фальшивая (8) и тяжелее): фальшивая монета (8) и тяжелее;
(возможна только если фальшивая (7) и тяжелее): фальшивая монета (7) и тяжелее;
-
(возможно только если фальшивая среди (1) и (2) и легче):
(возможна только если фальшивая (1) и легче): фальшивая монета (1) и легче;
(возможна только если фальшивая (2) и легче): фальшивая монета (2) и легче;
-
(возможно только если фальшивая среди (5) и (6) и тяжелее):
(возможна только если фальшивая (6) и тяжелее): фальшивая монета (6) и тяжелее;
(возможна только если фальшивая (5) и тяжелее): фальшивая монета (5) и тяжелее;
(то есть фальшивая среди
и тяжелее, или среди
и легче, а все
— настоящие):
-
(то есть фальшивая среди (4) и тяжелее, или (7) и (8) и легче, а все остальные монеты — настоящие):
(возможно только если фальшивая (4) и тяжелее): фальшивая монета (4) и тяжелее;
(возможна только если фальшивая (7) и легче): фальшивая монета (7) и легче;
(возможна только если фальшивая (8) и легче): фальшивая монета (8) и легче;
-
(возможно только если фальшивая среди (3) и тяжелее или (5) и (6) и легче):
(возможно только если фальшивая (3) и тяжелее): фальшивая монета (3) и тяжелее;
(возможна только если фальшивая (5) и легче): фальшивая монета (5) и легче;
(возможна только если фальшивая (6) и легче): фальшивая монета (6) и легче;
-
(возможно только если фальшивая среди (1) и (2) и тяжелее):
(возможна только если фальшивая (2) и тяжелее): фальшивая монета (2) и тяжелее;
(возможна только если фальшивая (1) и тяжелее): фальшивая монета (1) и тяжелее.
Итак, искомое
Ошибка.
Попробуйте повторить позже
Нынешний год — високосный, то есть февраля
г.
— реальная календарная дата. Сколько (вещественных) корней (и
какой кратности) имеет уравнение
Источники:
Подсказка 1
Рассмотрим функцию f(x) = x³ + 29x² + 2x + 20. Давайте начнем с того, имеет ли она хотя бы 1 корень.
Подсказка 2
Это кубическая функция с положительным коэффициентом при старшей степени. Если взять какой-то достаточно малый x, значение будет отрицательным, аналогично можно получить и положительное значение. Следовательно, функция хотя бы 1 раз пересекает ось OX и имеет 1 корень. Как, исходя из этого, можно доказать наличие других корней?
Подсказка 3
Если она в каком-то месте перегнется, то, возможно, вновь пересечет ось OX и будет новый корень. Посмотрите на производную этой функции.
Подсказка 4
f'(x) = 3x² + 58x + 2. x₁¸₂ = ( -29 ± √835 ) / 3. Это точки перегиба функции. Попробуйте посмотреть, какие значения f принимает в них. Заметьте, что для упрощения вычислений в f можно выделить производную (в точках x₁ и x₂ она равна нулю).
Подсказка 5
У вас получится x₂ < x₁, f(x₁) > 0, f(x₂) > 0. Разделите прямую на 3 части точками x₁ и x₂ и поймите, возрастает/убывает ли там функция, какие значения принимает (положительные/отрицательные).
Рассмотрим функцию Это кубическая функция с положительным коэффициентом при старшей степени, то есть
при очень маленьких значениях аргумента(например, при
) функия будет отрицательной, а при очень больших значениях
аргумента — положительной. Таким образом, функция имеет хотя бы один корень. Осталось проверить, есть ли ещё корни. Рассмотрим
производную:
Найдём её корни: дискриминант квадратного уравнения равен
откуда
Тогда корни равны
и
Теперь посчитаем значение в точках
и
В этих точках производная равна нулю, поэтому попробуем выделить её для
упрощения вычислений:
Получается,
Заметим, что откуда
— отрицательное число, которое при умножении на отрицательное
становится положительным. Таким образом,
— это сумма двух положительных чисел, то есть
Теперь подставим
Так как то
Отсюда, аналогично рассуждениям про
получаем
Итак, и
Получается, что
возрастает на промежутке
При этом функция отрицательна на
очень маленьких значениях из этого промежутка и положительна в точке
откуда функция равна нулю на какой-то точке этого
промежутка. Далее, функция убывает на
при этом она положительна в этих точках, а, значит, положительна и на всём этом
промежутке. Наконец,
возрастает на
то есть для любого
выполняется, что
откуда на этом
промежутке функция так же положительна.
Таким образом, уравнение имеет ровно один вещественный корень.
Не более одного вещественного корня
Ошибка.
Попробуйте повторить позже
Во время собеседования при приеме на работу в разных IT-компаниях любят задавать разные тестовые нестандартные задачи для проверки творческих способностей кандидата на работу. Одна из таких популярных тестовых задач следующая (см. рисунок):
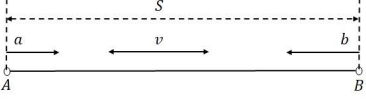
Точки и
двигаются на встречу друг-другу (обычно говорят о двух «путниках») со скоростями
и
соответственно, а между
ними все время «летает» со скоростью
и
еще одна точка (обычно говорят о «мухе», которая летает с носа одного путника
на нос другого путника без задержек на носу ни одного из путников). Начальное расстояние между точками
и
равно
Вопрос: какое расстояние пролетит точка-муха от момента начала движения точек-путников до момента их
встречи?
Так вот, в этой задаче вам сначала надо ответить на вопрос, сформулированный в тестовой задаче: какое расстояние пролетит точка-муха от момента начала движения точек-путников до момента их встречи? Далее, вам надо ответить на следующий вопрос (и доказать ответ!): конечное или бесконечное число полетов между точкам-путниками совершит точка-муха от момента начала движения до момента встречи точек-путников?
И, наконец, вам надо ответить на еще один вопрос. Пусть в начальный момент точка-муха находилась в точке Какое суммарное
расстояние пролетит точка-муха, когда движется от
до
А какое суммарное расстояние пролетит точка-муха, когда движется от
до
Источники:
Вопрос 1, подсказка 1
Сначала можно вычислить время, которое будет летать точка-муха, а потом уже найти расстояние.
Вопрос 2, подсказка 1
Предположим, что точка-муха совершила конечное число полетов, тогда мы либо докажем это, либо получим противоречие.
Вопрос 2, подсказка 2
Попробуйте рассмотреть последний полет точки-мухи.
Вопрос 2, подсказка 3
Пусть последний полет был от точки А. Какие будут скорости у точки А и у точки-мухи?
Вопрос 2, подсказка 4
У точки-мухи будет скорость v, у точки А — a. Какая из этих точек прилетит раньше в точку встречи точек-путников?
Вопрос 2, подсказка 5
Сравните скорости a и v, опираясь на условие, и проведите аналогичные рассуждения в случае, если последний полет точки-мухи происходит от точки B.
Вопрос 3, подсказка 1
Давайте попробуем составить формулы расстояний перелетов в общем виде. Для этого можно посчитать расстояния в конкретных ситуациях.
Вопрос 3, подсказка 2
В некоторый момент времени точка-муха находится в точке А, пусть в этот момент расстояние между A и B равно p₀. Через какое время точка-муха окажется в точке B?
Вопрос 3, подсказка 3
t₁ = p₀ / (v + b). Какое расстояние при этом пролетит точка-муха?
Вопрос 3, подсказка 4
w₁ = t₁v = p₀v / (v + b). Чему будет равно расстояние между точками A и B после полета?
Вопрос 3, подсказка 5
p₁ = p₀ - t₁(a + b) = p₀ ⋅ (v - a) / (v + b). Через какое время точка-муха вновь окажется в точке А?
Вопрос 3, подсказка 6
t₂ = p₁ / (v + a) = p₀ ⋅ (v - a) / ((v + a)⋅(v + b)). Какое расстояние она пролетит от B к A?
Вопрос 3, подсказка 7
w₂ = t₂v = p₀ ⋅ (v - a) ⋅ v / ((v + a)⋅(v + b)). Какое расстояние между точками A и B после этого?
Вопрос 3, подсказка 8
p₂ = p₁ - t₂(a + b) = p₀ ⋅ (v - a)(v - b) / ((v + a)(v + b)). Посмотрите на полученные результаты и попробуйте записать в общем виде формулы для расстояний между точками A и B до и после k-го перелета.
Вопрос 3, подсказка 9
Теперь вспомним, что мы хотим найти. Запишите формулы для расстояний, которые будет пролетать точка-муха.
Вопрос 3, подсказка 10
Рассмотрим случай, когда точка-муха летит от A к B. Заметьте, что расстояния, которые будет пролетать точка-муха, образуют бесконечно убывающую геометрическую прогрессию.
Вопрос 3, подсказка 11
Ее суммой и будет суммарное расстоние, которое пролетит точка-муха от A до B. Чтобы найти суммарное расстояние, которое пролетит точка-муха от B к A, для начала посчитайте общее расстояние, которое пролетит точка-муха.
Первый вопрос.
Общее время движения точек-путников
поэтому расстояние, которое пролетит точка-муха за это время
Второй вопрос.
Давайте предположим, что точка-муха совершит некоторое конечное число полетов между точками-путниками. Тогда либо мы докажем это, либо прийдем к противоречию и получим, что полетов было бесконечное количество.
Рассмотрим последний полет точки-мухи между точками-путниками. Если это был полет от точки движущейся направо со
скоростью
то, так как это был последний полет, точка-муха тоже летит направо со скоростью
и прилетает в точку встречи
точек-путников не раньше точки
то есть скорость точки-мухи
которая не больше скорости
Получаем противоречие с тем, что Аналогично получаем противоречие в случае, если последний полет точки-мухи происходит от
точки
Следовательно, предположение о конечном числе полетов неверно.
Третий вопрос.
Пусть в некоторый момент времени точка-муха находится в точке и в это время расстояние между точками
и
равно
Тогда точка-муха окажется в точке
спустя время
при этом точка-муха пролетит расстояние
в направлении от к
а расстояние между точками
и
после полета будет равно
Точка-муха вновь окажется в точке спустя время
Она пролетит в направлении от к
После этого расстояние между точками и
будет равно
Следовательно, для любого мы имеем: расстояние между точками
и
после
перелета
-
от
до
равно
-
от
до
равно
Теперь заметим, что для любого расстояние между точками перед
перелетом
-
от
до
равно
-
от
до
равно
Тогда для любого расстояние, которое пролетит точка-муха в
раз,
-
от
до
равно
-
от
до
равно
— бесконечно убывающая геометрическая прогрессия с первым членом
и знаменателем
Сумма прогрессии равна
Это и есть суммарное расстояние, которое пролетит точка-муха, когда движется от до
Так как общее расстояние, которое пролетит точка-муха, равно
то, следовательно, суммарное расстояние, которое пролетит точка-муха, когда движется от к
равно
1) 2) Бесконечное; 3)
Ошибка.
Попробуйте повторить позже
Окружность — это, как известно, множество точек на плоскости, удаленных от заданной точки (центра) на фиксированное расстояние
(радиус окружности), а число — это отношение длинны окружности к длине ее диаметра. В этом определении по умолчанию
предполагают, что речь идет об Евклидовом расстоянии/длине, которая вычисляется на двумерной координатной плоскости
для
отрезка с концами в точках
и
по формуле
Однако, Евклидово определение
длины — не единственно-возможное. Например, манхэттенская длина отрезка с концами в точках
и
вычисляется по формуле
(Название «манхэттенское расстояние» связано с уличной планировкой
Манхэттена, представляющую собой прямоугольную сетку улиц: «На север с юга идут авеню, на запад с востока — стриты» В. В.
Маяковский, «Бродвей».) Чему равно отношение манхэттенской длинны Евклидовой окружности к манхэттенской длине ее
диаметра?
Источники:
Подсказка 1
Для начала было бы сподручно вообще понять, что из себя представляет махэттенская длина Евклидовой окружности. Да, из условия задачи знаем определение манхэттенской длины, но надо понять, как с её помощью посчитать длину окружности. Может, есть какая-то закономерность между манхэттенской длиной цепочки точек и длиной лишь между первой и последней из этих точек?
Подсказка 2
Не забудьте доказать, что связь, полученная вами, верна для всех случаев. Попробуйте рассмотреть дугу Евклидовой окружности в 90°. А что будет если соединить все точки этой дуги непрерывной ломаной? Как посчитать её манхэттенскую длину?
Подсказка 3
Осталось только обобщить полученный вами результат на всю окружность, и дальше дело элементарной арифметики :)
Рассмотрим произвольную ломаную (см. рисунок) такую, что абсциссы ее узлов ведут себя монотонно (на рисунке они не убывают) и ординаты ее узлов тоже ведут себя (возможно, по-другому, но тоже) монотонно (на рисунке они тоже не убывают). Тогда манхэттенская длина такой ломаной (то есть сумма манхэттенских длин ее отрезков) равна манхэттенскому расстоянию между ее концами.
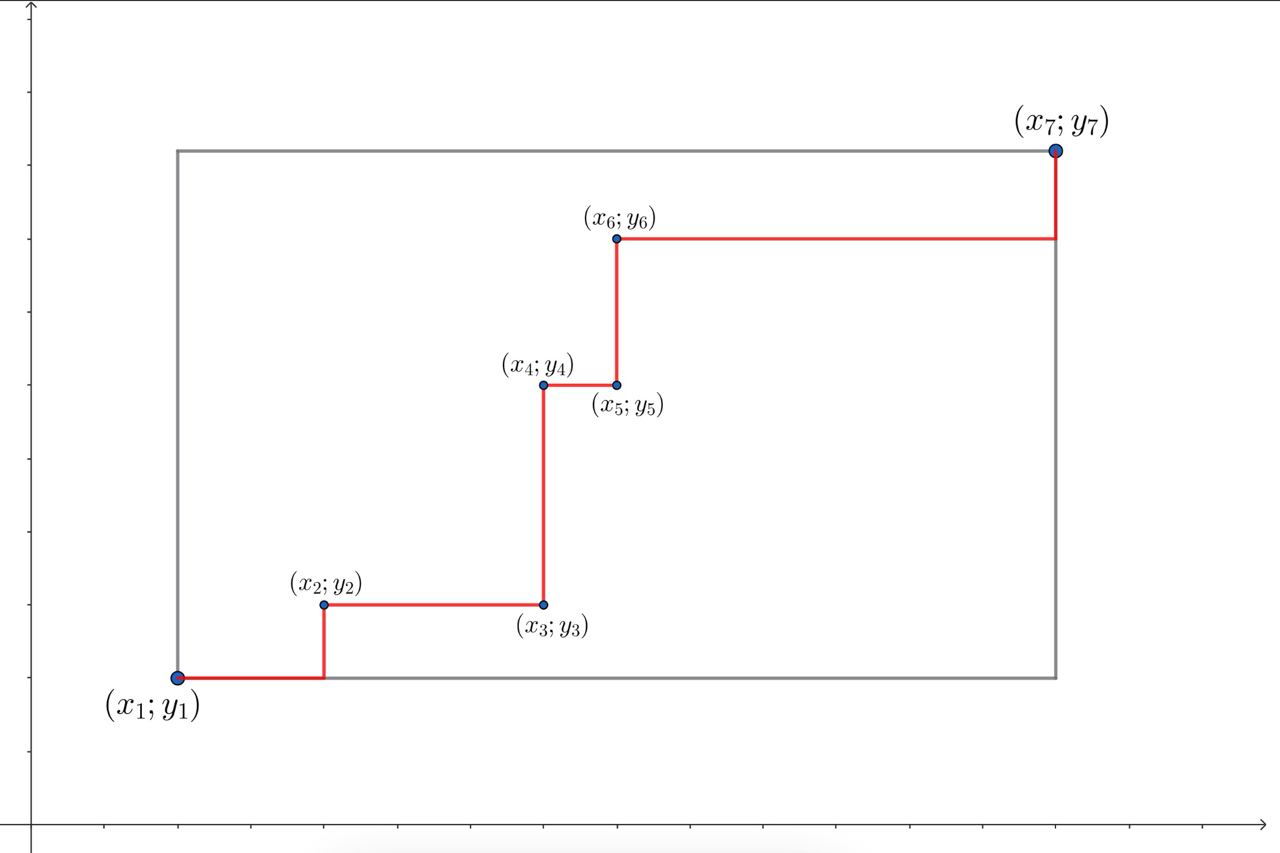
Доказательство этого утверждения должно рассматривать разные варианты (абсциссы и ординаты не убывают, абсциссы не убывают, а ординаты не возрастают, и так далее), но мы ограничимся только случаем, представленном на рисунке:
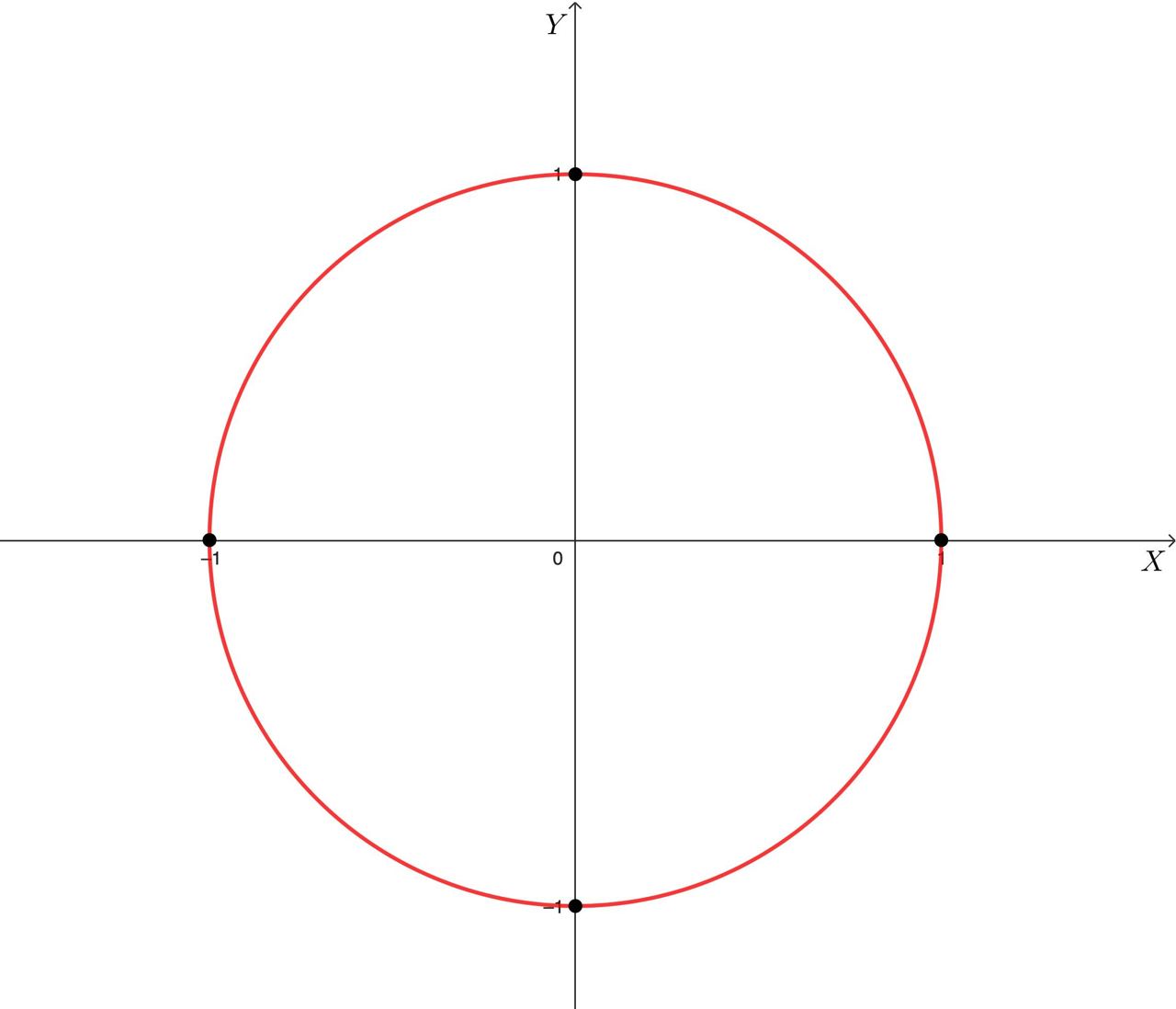
Следовательно, манхэттенская длина каждого из четырех сегментов
и
евклидовой окружности манхэттенского радиуса 1 с центром в начале координат равны
манхэттенская длина всей этой Евклидовой окружности равна а отношение манхэттенской длины Евклидовой окружности к
манхэттенской длине ее диаметра равно

