Тема ОММО - задания по годам

ОММО 2014

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела оммо - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#31833Максимум баллов за задание: 7

Натуральное $61$ -значное число $A$ записывается только цифрами $2$ , $3$ и $4$ . При этом двоек на $19$ больше, чем четверок. Найдите остаток от деления числа $A$ на $9$ .

Источники: ОММО-2014, номер 3, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Давайте вспомним, чему равен остаток от деления числа на 9.

Подсказка 2

При делении на 9 остаток равен остатку от деления суммы его цифр на 9. Тогда давайте найдем её.

Подсказка 3

Пускай двоек было x, тогда четверок было x - 19, а троек 61 - 2x + 19 = 80 - 2x. Теперь можно найти сумму цифр и остаток от деления на 9.

Показать ответ и решение

Пусть в числе $a$ двоек, $b$ троек, $a− 19$ четвёрок. Тогда всего цифр $2a +b− 19= 61 ⇐⇒ 2a+ b= 80$ . При делении на $9$ число даёт такой же остаток, какой даёт его сумма цифр, то есть

2⋅a+ 3⋅b+4 ⋅(a− 19)=6a+ 3b− 76 =3⋅80− 76= 164≡9 2

Ответ:

$2$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#47135Максимум баллов за задание: 7

Дан выпуклый пятиугольник $ABCDE$ . Точки $M, N,P$ и $Q−$ середины сторон $AB,BC,CD$ и $DE$ соответственно, точки $H$ и $K$ — середины $MP$ и $NQ$ соответственно. Найдите длину отрезка $HK$ , если $AE = 7$ .

Источники: ОММО-2014, номер 4, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1!

Попробуем отрезок MQ выразить двумя разными способами, чтобы приравнять и вычислить HK. Для этого в вычислениях должен встречаться HK. Попробуйте записать MQ двумя различными способами

Подсказка 2!

Например, как две покрывающие его ломаные, например, MH + HK + KQ. И вторая ломаная, MB + BC + CD + DQ

Подсказка 3!

То есть теперь попробуем выразить все отрезки через AB, BC, CD, DE и отношения с ними, а Hk оставить нетронутым, чтобы выразить!

Показать ответ и решение

$PIC$

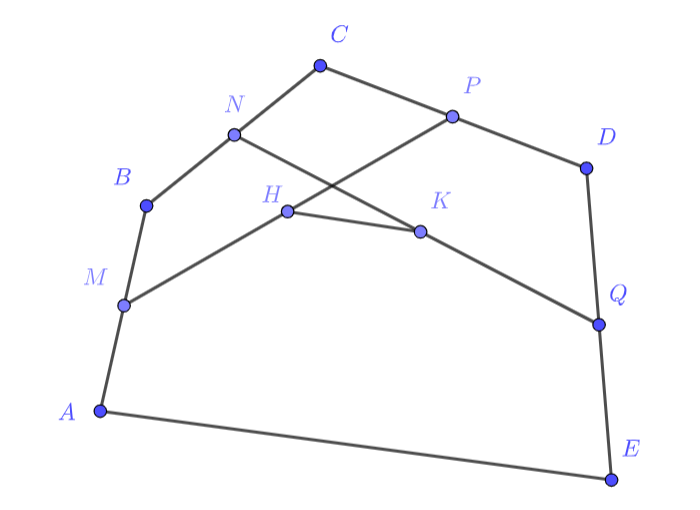
Опустим везде обозначения векторов, поскольку больше ничего использовать не будем. Выразим $MQ$ двумя способами

MQ = MH + HK + KQ = MB + BC +CD + DQ = AB-+ BC+ CD + DE- (1) 2 2

Распишем более подробно первое равенство

MP- -A2B+-BC-+-CD2- NQ- -B2C+-CD-+-DE2- MH = 2 = 2 ; KQ = 2 = 2

AB 3BC 3CD DE MQ = NH +HK +KQ =-4- +--4-+ --4-+ -4-+ HK (2)

Приравнивая $(1)$ и $(2)$ , имеем

AB + BC +CD + DE AE |AE | 7 HK = --------4--------= -4- =⇒ |HK |= -4--= 4

Ответ:

$7 4$

Ошибка.
Попробуйте повторить позже

Задача 3#47250Максимум баллов за задание: 7

Найдите все решения уравнения

2 2 2 (y(x− 1)) +(x− 1) +y + 1− 4y|x− 1|= 0.

Источники: ОММО-2014, номер 5, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Вспомним, что (x - 1)² эквивалентно |x - 1|². Чем нам это может помочь?

Подсказка 2

Для начала введем замену на модуль, проведем соответствующие преобразования и приведем подобные. Что теперь можно заметить?

Подсказка 3

Оставьте с одной стороны произведение двух выражений, а вправо вынесите одно слагаемое. Есть ли теперь предположения о количестве решений? Что можно сказать про каждую из частей равенства?

Подсказка 4

Можно действовать "в лоб": сравнить правую и левую части с модулем правой. Логично, что правая часть будет меньше либо равна своего модуля. А что насчет левой?

Подсказка 5

Тут нужно либо решить квадратное относительно переменной yt, либо понять, что a² + 1 = 2|a| только в случае a = 1. Отсюда мы уже получаем необходимые значения t и y и делаем обратную замену.

Показать ответ и решение

Заменим $t= |x − 1|≥ 0$ , а также перепишем уравнение в виде

2 2 (y + 1)(t +1)= 4yt

Как известно $a2+ 1≥2|a|$ , при этом $a2+ 1= 2|a| ⇐⇒ |a|= 1$ , откуда

2 2 4yt= (y + 1)(t + 1)≥ 4|yt|=4t|y|

и равенство достигается тогда и только тогда, когда $|y|=|t|= 1$ , при этом $|y|= y$ , поскольку иначе $4yt⁄=4t|y|$ . Получаем $y =1,|x − 1|= 1 ⇐ ⇒ x ∈{0,2}$ .

Ответ:

$(0;1);(2;1)$

Ошибка.
Попробуйте повторить позже

Задача 4#49754Максимум баллов за задание: 7

Диагонали трапеции взаимно перпендикулярны, а боковые стороны образуют угол $30∘$ . Основания имеют длины $6$ и $2.$ Найдите высоту трапеции.

Подсказки к задаче

Подсказка 1

Нам нужно найти высоту трапеции. Давайте подумаем, как это будет проще всего сделать. Например, если обозначить угол между основанием и диагональю за α, то высота это BD * sinα. А как можно выразить диагональ, зная угол?

Подсказка 2

Ага, так как диагонали перпендикулярны, то образуются прямоугольные треугольники, и все отрезки диагоналей легко выражаются через α. Выходит, что высота это 8cos(α)sin(α). Теперь наша задача найти угол α. Какое дополнительное построение удобно сделать в данном случае, зная угол между боковыми сторонами?

Подсказка 3

Верно, давайте достроим нашу трапецию до параллелограмма. Получается треугольник с углом при вершине в 30 градусов. Заметим, что все его стороны мы можем выразить из прямоугольных треугольников внутри трапеции, используя только угол α. Какой добивающей теоремой теперь можно воспользоваться?

Подсказка 4

Да, воспользуемся теоремой косинусов, потому что все стороны и угол в 30 градусов нам известны. Осталось только аккуратно найти α и выразить высоту. Победа!

Показать ответ и решение

$PIC$

Пусть эта трапеция $ABCD, BC = 2,AD =6$ . При этом $AB ∩CD = X,∠AXD =30∘$ , а также $AC ∩BD =O,AC ⊥ BD$ .

Построим $DN ∥AB,N ∈ BC$ , тогда $∠CDN = 30∘$ , $DN = AB$ . Кроме того, из $AD =BN$ получаем $CN =4$ . Введём также $∠ADB =α$ . Используем прямой угол между диагоналями $AO = 6sinα,OD = 6cosα,OC = 2sinα,OB = 2cosα$ . Отсюда $∘ -------------- ∘ --------- ---- CD = 4sin2α+ 36cos2α= 4+ 32sin2α = √4+ t$ , $∘ -------------- ----- AB = DN = 36sin2α+ 4cos2α= √ 36 − t$ ( $t= 32sin2α$ ). Теперь мы готовы написать теорему косинусов для $△CDN$

CD2 + DN2 − 2CD ⋅DN cos∠CDN = CN2

√- 36 − t+ 4+ t− 2∘ (4+-t)(16− t)⋅-3-= 16 2

√ -- (4+ t)(16 − t)= 192 ⇐⇒ t2− 32t+ 48 =0 ⇐ ⇒ t= 16± 4√13- =⇒ sin2α = 4±--13 8

Оба значения подходят, поскольку обозначения в условии симметричны. Не умаляя общности, $∘ 4+√13 sinα= 8$ , откуда $∘ --√-- cosα= 4−813$ . Осталось заметить, что высота трапеции равна $∘ --√-----√--- √- BDsinα= 8cosα sinα= 8 (4−-13)(644+-13)= 3.$

Ответ:

$√3$

Ошибка.
Попробуйте повторить позже

Задача 5#58040Максимум баллов за задание: 7

В городе $200$ жителей. Часть из них — рыцари, которые всегда говорят правду, остальные — лжецы, которые всегда лгут. Каждый горожанин живет в одном из четырех кварталов (А, Б, В и Г). Каждому задали четыре вопроса: “Вы живете в квартале А?”, “Вы живете в квартале Б?”, “Вы живете в квартале В?”, “Вы живете в квартале Г?”. На первый вопрос утвердительно ответило $105$ жителей, на второй — $45$ , на третий — $85$ и на четвёртый — $65.$ В каком квартале лжецов живет больше, чем рыцарей и на сколько?

Источники: ОММО-2014, задача 9 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Давайте попробуем составить уравнения на количество рыцарей и лжецов в каждом квартале. Например, пусть x₁ это количество рыцарей в первом квартале, а у₁ это количество лжецов в нем. И так же сделаем для остальных кварталов. Тогда попробуйте переписать условия по количеству ответов в виде уравнений!

Подсказка 2

У нас должна получиться такие уравнения!
x₁ + y₂ +y₃ + y₄ = 105
x₂+ y₁+y₃+ y₄ = 45
x₃+ y₁+y₂+ y₄ = 85
x₄+ y₁+y₂+ y₃ = 65
Но так как у нас в каждом уравнении почти сумма всех у, попробуйте обозначить у = y₁+y₃+ y₄ + y₂. И подставим это в наши уравнения!

Подсказка 3

Теперь в каждом уравнении встречается xₐ- yₐ. А это как раз то, что нас интересует - разница между лжецами и рыцарями. Давайте сделаем еще одну замену на z₁ = x₁ - y₁ для каждого квартала.

Показать ответ и решение

Первое решение.

На четыре вопроса каждый рыцарь даёт один утвердительный ответ, а лжец — три. Всего было получено $105+ 45 +85+ 65= 300$ утвердительных ответов. Если бы все жители города были рыцарями, в сумме всех утвердительных ответов было бы 200. 100 лишних ответов «да» происходят от вранья лжецов. Таким образом, лжецов $100- 2 =50$ . Пусть в квартале Б живет $k$ рыцарей, тогда $45 − k$ —число утвердительных ответов на второй вопрос, которые дали лжецы. Значит число лжецов, живущих в квартале Б, равно $50− (45− k)= k+5$ . В остальных кварталах число лжецов меньше числа рыцарей.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Пусть $xk$ и $yk$ — количества рыцарей и лжецов в $k$ -м квартале из $4$ соответственно, $x$ — рыцарей всего, $y = 200− x$ — лжецов всего. Тогда

( ( ||||{ x1+ y2+y3+ y4 = 105 ||||{ x1+ y− y1 = 105 x2+ y1+y3+ y4 = 45 =⇒ x2+ y− y2 = 45 ||||( x3+ y1+y2+ y4 = 85 ||||( x3+ y− y3 = 85 x4+ y1+y2+ y3 = 65 x4+ y− y4 = 65

Введём обозначения $zk = yk− xk$ — насколько в $k$ квартале больше лжецов, получим

( ||||{ y = 105+ z1 y = 45 +z2 ||||( y = 85 +z3 y = 65 +z4

В итоге наибольшее $zk$ достигается для $k= 2$ . Далее просуммируем уравнения, получим

4y =300+ y− x ⇐⇒ 3y =300− x= 300− 200+ y ⇐⇒ y = 50

Имеем $(z1,z2,z3,z4)= (− 55,5,− 35,−15)$ . Отсюда лжецов больше только во втором квартале на $5$ .

Ответ:

в квартале Б на $5$

Ошибка.
Попробуйте повторить позже

Задача 6#64568Максимум баллов за задание: 7

В прямоугольном параллелепипеде $ABCDA B C D 1 1 1 1$ с рёбрами $AB =3,AD = 4$ и $AA = 5 1$ проведены два сечения – плоскостью, проходящей через диагональ $A1C$ , и плоскостью, проходящей через диагональ $B1D$ . Найдите наибольшее возможное значение суммы площадей поверхностей многогранников, на которые эти сечения разбивают данный параллелепипед.

Источники: ОММО-2014, номер 10, (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Нарисуйте картинку и попробуйте понять: что точно, вне зависимости от положения сечений будет содержаться в искомой сумме? Можем ли мы как-то избежать попадания в эту сумму какой-то части исходного параллелепипеда? А сколько раз туда попадут части наших сечений?

Подсказка 2

Итак, получается, что как бы ни были расположены сечения, их площади дважды войдут в искомые площади поверхностей. Значит надо эти площади максимизировать!

Подсказка 3

Какой фигурой будет являться каждое сечение? Как площади сечений связаны с длинами диагоналей? Исследуйте, где должны быть расположены вершины параллелограмма-сечения, чтобы расстояние до диагонали параллелепипеда было наибольшим.

Подсказка 4

Осталось лишь посчитать все нужные длины, призвав на помощь теорему Пифагора. Будьте внимательны к арифметике и задача окажется убита!

Показать ответ и решение

Сумма площадей поверхностей многогранников, на которые разбивается параллелепипед сечениями, равна сумме площади поверхности параллелепипеда и площадей внутренних поверхностей. Сумма площадей внутренних поверхностей равна удвоенной сумме площадей сечений.

Найдем наибольшую возможную площадь сечения, проходящего через диагональ $XY$ произвольного параллелепипеда с ребрами $a≤ b≤ c$ . Сечением является параллелограмм $ZXT Y$ , вершины которого лежат на противоположных рёбрах параллелепипеда. Площадь параллелограмма равна произведению длины диагонали $XY$ на расстояние от точки $Z$ до $XY$ .

$PIC$

Рассмотрим проекцию параллелепипеда на плоскость, перпендикулярную диагонали $XY$ . На рисунке видно, что расстояние от точки $Z$ ломаной $ABC$ до точки $Y$ , то есть до диагонали $XY$ , наибольшее, если $Z$ совпадает с одной из вершин $A,B$ или $C$ .

$PIC$

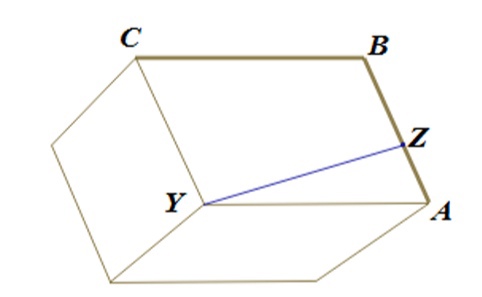
Значит, сечение проходит через одно из ребер параллелепипеда. Таким образом, наибольшую площадь имеет одно из диагональных сечений. Все эти сечения являются прямоугольниками. Найдем наибольшую из их площадей

∘----- ∘------ ∘ ------ S1 = a b2+ c2,S2 = b a2+ c2 и S3 =c b2+ a2.

Из условия $a ≤b ≤c$ следует, что, $22 22 2 2 2 2 a b +a c ≤c b +a c$ , и $22 22 22 22 a b+ c b ≤c b+ a c$ . Поэтому $S1 ≤ S3$ и $S2 ≤ S3$ . Значит, наибольшую площадь имеет сечение, проходящее через наибольшее ребро. По условию наибольшую длину имеет ребро $AA1$ , значит, наибольшую площадь $√-2---2 5 4 + 3 = 25$ имеют сечения $AA1C1C$ и $BB1D1D$ .

$PIC$

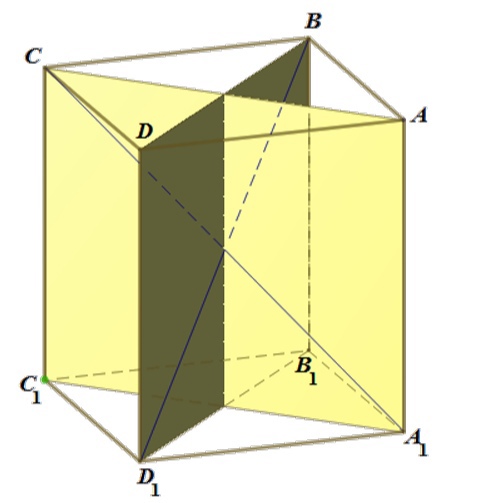
Сумма площадей поверхностей многогранников, на которые разбивается параллелепипед этими сечениями (см. рисунок), равна

2(AA1⋅AB + AA1⋅AD +AB ⋅AD )+4 ⋅25= 194.

Ответ: 194

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#80511Максимум баллов за задание: 7

Даны 2014 положительных чисел. Известно, что произведение любых тридцати пяти из них меньше единицы. Докажите, что произведение всех данных чисел меньше единицы.

Подсказки к задаче

Подсказка 1

Если перемножить набор выражений, каждое из которых меньше единицы, то произведение будет тоже меньше единицы!

Подсказка 2

Мы знаем, что произведение любых 35 чисел меньше единицы. Какие удобные числа мы можем выбрать?

Подсказка 3

Давайте запишем систему неравенств. Сначала возьмём первые 35 чисел, потом набор из следующих 35 чисел и т.д..

Показать доказательство

Пусть даны числа $x ,x,...,x 1 2 2014$ . Тогда

x1x2⋅...⋅x35 < 1

x x ⋅...⋅x < 1 2 3 36

...

x1981x1982⋅...⋅x2014x1 < 1

Перемножим все эти неравенства и получится

(x1x2...x2014)34 <1

Тогда

x1x2...x2014 < 1

Ошибка.
Попробуйте повторить позже

Задача 8#90848Максимум баллов за задание: 7

Найдите все значения параметра $a$ , при которых уравнение

|ln |x||= ax

имеет три решения.

Подсказки к задаче

Подсказка 1

Попробуйте найти симметрию.

Подсказка 2

Нетрудно заметить, что случаи a > 0 и a < 0 симметричны с точностью до знака x. Тогда рассматриваем случай положительного a. Что можно о нем сказать?

Подсказка 3

Логично, что x тогда тоже положительный. Тогда |x| = x, теперь мы можем построить график |ln(x)| и посмотреть на его пересечения с пучком прямых ax. Посмотрим на сам график. Какие "значимые" точки мы можем заметить?

Подсказка 4

Видим, что решения могут быть только в первой четверти, а также то, что в целом максимум может быть 3 решения (3 точки пересечения), при этом все эти случаи ограничены одним углом, образованным прямыми из пучка. Какие это прямые?

Подсказка 5

Получаем граничные случаи, а именно касание графика логарифма для x > 1 и параллельность оси x. Находим соответствующие этим случаям значения параметра и учитываем, что нам подходят все значения, лежащие между граничными.

Показать ответ и решение

Рассмотрим случай $a >0$ . Так как $0≤ |ln|x||=ax$ , то и $x> 0$ и поэтому $|x|= x$ . Построим график функции $y = |lnx|$ . Прямая $y =ax$ должна пересекать этот график в трех точках.

$PIC$

На рисунке видно, что это выполняется тогда и только тогда, когда прямая проходит внутри угла, образованного осью абсцисс и касательной $y = a0x$ к графику функции $y = lnx$ при $x> 1$ .