ОММО 2012
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Функция для всех
удовлетворяет равенству
а при задаётся формулой
. Найдите
Источники:
Подсказка 1
Из условия видно, что мы можем с помощью "наращивания" искать значения от сколь угодно больших аргументов, но нам бы хотелось делать это еще и как-то удобно и быстро. В этом нам мешает слагаемое x в выражении f(x+3)=x+2-f(x). Но, кажется, при повторении этой операции из-за минуса x должен уйти...
Подсказка 2
Действительно, f(x+6)=3+f(x). Тогда с помощью индукции можно установить, что f(x+6k)=3k+f(x). Как нам тогда найти f(2012)?
Подсказка 3
f(2012)=f(2+6*335), поэтому f(2012)=1005+f(2). Найдите f(2) и завершите решение!
Применим условие дважды
Используя это, получим
Ошибка.
Попробуйте повторить позже
На первом складе в каждом ящике в среднем по 3 бракованных изделия, а на втором складе — по 6. С первого склада на второй перевезли 50 ящиков, и среднее количество бракованных изделий в ящике на каждом из складов уменьшилось на 1. Сколько всего ящиков на двух складах?
Источники:
Подсказка 1
Мы понимаем, что количество бракованных деталей от перевозки ящиков не поменялось, а значит, данная задача подразумевает подсчет двумя способами количества наших бракованных деталей. Подумайте, как его тут можно реализовать и использовать?
Подсказка 2
Если мы обозначим количество ящиков за m для первого завода и за n для второго, то в первоначальном состоянии у нас было 3m и 6n бракованных деталей. После перевоза ящиков на первом заводе их стало m-50, а на втором n+50, при этом количество бракованных деталей на каждый ящик стало 2 и 5 соответственно. Зная всё это, составьте и решите уравнение.
Пусть на первом складе было ящиков, а на втором
. Бракованных деталей при этом имелось в общей сложности
на первом
складе и
на втором. После того, как ящики перенесли, средние значения стали равны
и
, а ящиков стало
и
соответственно. Общее число бракованных деталей теперь равно
, но оно осталось прежним, то есть
равным
. Приравнивая обе величины, получаем
и это есть общее число ящиков на двух складах
вместе.
Ошибка.
Попробуйте повторить позже
Решите систему
Подсказка 1
Давайте подумаем, что мы можем здесь сделать. Если не брать правые части уравнений, то выражения симметричны относительно переменных, которые в нем содержатся(хотя это вовсе не значит, что система симметрична). Это значит, что мы можем каким-то образом привести наши уравнения к нужному виду так, чтобы наши выражения относительно каждой из переменных были симметричны(то есть, на данный момент у нас в левой части каждого уравнения находится некоторое выражение, которое зависит и от x и от y(к примеру), а мы хотим, чтобы слева была сумма двух структурно одинаковых выражений, каждое из которых зависит только от одной переменной, ведь тогда мы сможем, сделав замену, просто-напросто решить линейную систему и все). Как это можно сделать?
Подсказка 2
Попробуйте перевернуть каждую из дробей слева и написать систему в виде (x + z)/xz = 1/3. Как тогда можно по-другому написать каждое из наших выражений слева, чтобы получилась сумма, структурно одинаковых выражений?
Подсказка 3
Верно, нужно расписать каждую дробь, как сумму обратных к переменным. Тогда, у нас получится система линейных уравнений на три переменных, которую мы умеем решать.
"Перевернём" каждое из уравнений системы:
Преобразование равносильно, т.к. ни одна из правых частей не может обратиться в ноль.
Заметим, что и т.д.
Поэтому мы получили систему линейных уравнений на и
Решая её, получаем
Ошибка.
Попробуйте повторить позже
Длина медианы треугольника
равна 3, длины сторон
и
— 5 и 7 соответственно. Найдите площадь треугольника
Подсказка 1
Какие крутые дополнительные построения, связанные с медианой, мы с Вами знаем?
Подсказка 2
Например, можно удвоить медиану и получить параллелограмм.
Подсказка 3
Что можно сказать о площадях получившихся треугольников?
Подсказка 4
Некоторые из них будут равновеликими. Значит, можно вычислить площадь более "удобного".
Подсказка 5
Как найти площадь треугольника, все стороны которого известны?
Подсказка 6
Воспользуйтесь формулой Герона.
Продлим медиану за точку
до точки
такой, что
![]()
Получим треугольник , равновеликий исходному, со сторонами 5,6 и 7. Его площадь легко найти по формуле
Герона:
Ошибка.
Попробуйте повторить позже
На одной из сторон острого угла с вершиной взяты точки
и
, а на другой – точка
. При какой длине отрезка
величина
угла
максимальна, если
Подсказка 1
В таких задачах бывает полезно сделать какие-то дополнительные построения, на рисунке ведь почти ничего полезного нет. Какую конструкцию хочется добавить на картинку, чтобы одновременно и воспользоваться длинами отрезков, и было что-то связанное с углами?
Подсказка 2
Кажется, какие-то прямые строить не хочется, иначе уйдём в тяжёлый счёт, пытаясь связать длины отрезков с углами. Может быть, у нас есть на примете какие-то кривые?
Подсказка 3
Тут неплохим вариантом кажется построение окружности через точки A и B, касающейся другой стороны угла.
Подсказка 4
Кажется, что точка касания стороны угла и окружности и будет той самой точкой C, при которой угол ACB — максимален. Давайте попробуем это доказать.
Подсказка 5
Если мы возьмём точку, отличную от точки касания, то предполагаемый угол будет отсекать от окружности две дуги. Как градусная мера угла связана с градусными мерами этих дуг?
Подсказка 6
Такой угол равен полуразности большей и меньшей дуг, которые он отсекает. А значит, будет меньше угла ACB, где C — точка касания окружности и прямой. Осталось лишь найти величину отрезка OC.
Проведем через точки и
окружность, касающуюся второй стороны угла. Если
— точка касания, то угол
равен половине
дуги
В противном случае угол
равен полуразности дуги
и второй дуги, высекаемой углом
— т. е. будет меньше.
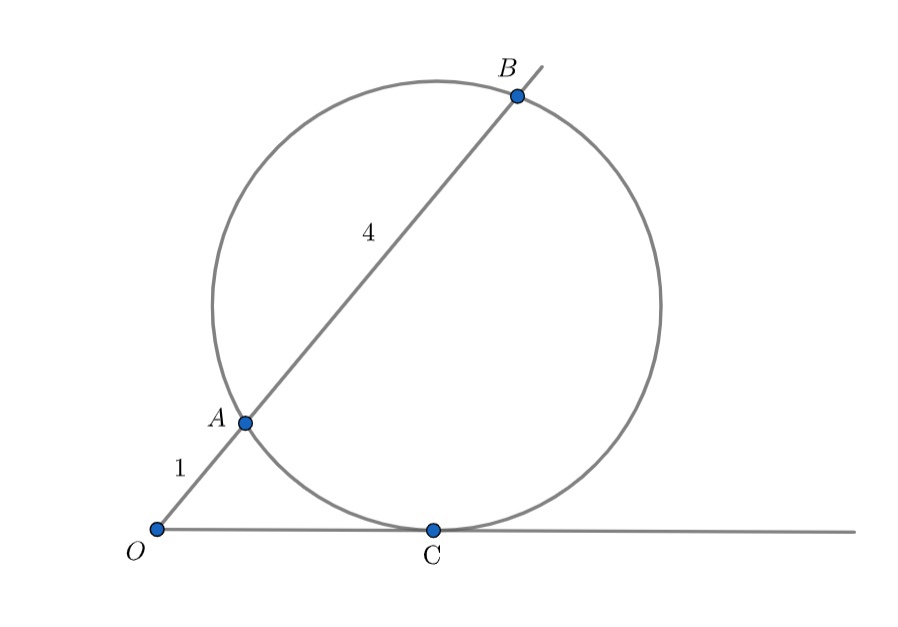
Остается воспользоваться тем, что квадрат касательной равен произведению секущей на ее внешнюю часть, откуда
.
Ошибка.
Попробуйте повторить позже
Посылка должна быть упакована в ящик в форме прямоугольного параллелепипеда и перевязана один раз вдоль и два раза поперек.
![]()
Можно ли отправить посылку объема 37 , имея 3,6 м веревки? (толщиной стенок ящика и уходящей на узлы веревкой
пренебречь)
Подсказка 1
Введём длины сторон коробки: x, y и z. Тогда можно легко выразить длину верёвки.
Подсказка 2
Длина веревки равна (с точностью до замены переменных) 2x + 6y + 4z.
Подсказка 3
Как легче всего оценить сумму нескольких слагаемых снизу?
Подсказка 4
Правильно, воспользуемся неравенством о средних и посмотрим, какое наименьшее значение длины может быть у верёвки.
Пусть ящик имеет размеры . Тогда веревка имеет длину
. Но по неравенству о средних

