04 Счет углов
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Чему равна сумма углов треугольника?
Источники:
Это фундаментальное свойство евклидовой геометрии, доказанное ещё в древности.
Ошибка.
Попробуйте повторить позже
Чему равна сумма смежных углов?
Источники:
Смежные углы всегда образуют развёрнутый угол, который равен
Ошибка.
Попробуйте повторить позже
Чему равен внешний угол треугольника?
Источники:
Это важное свойство вытекает из теоремы о сумме углов треугольника. =
+
Ошибка.
Попробуйте повторить позже
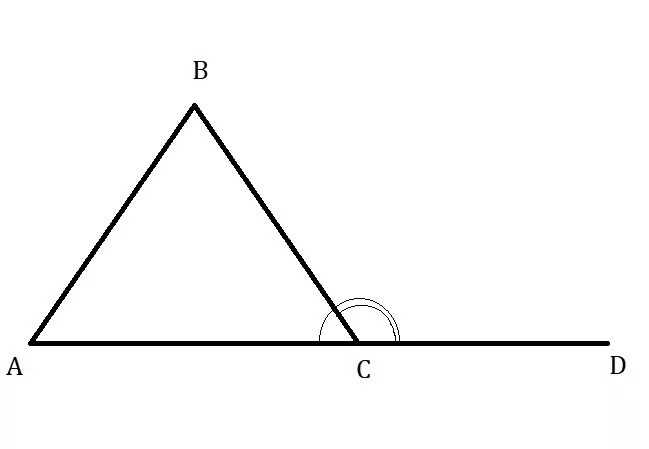
Внешний угол при вершине треугольника
равен
а внутренний угол
–
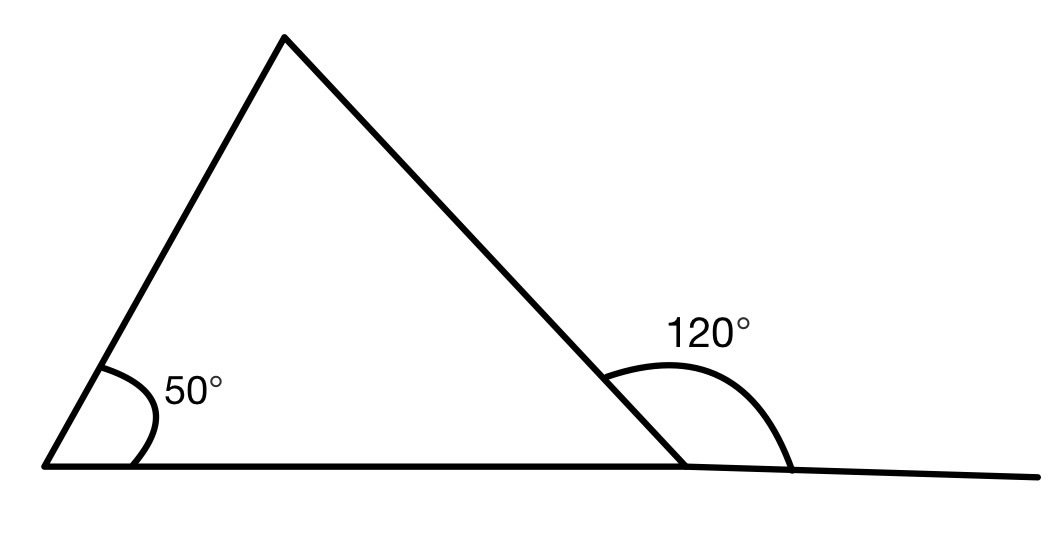
Чему равен угол
треугольника?
Источники:
Внешний угол треугольника равен сумме двух углов, не смежных с ним, то есть
Ошибка.
Попробуйте повторить позже
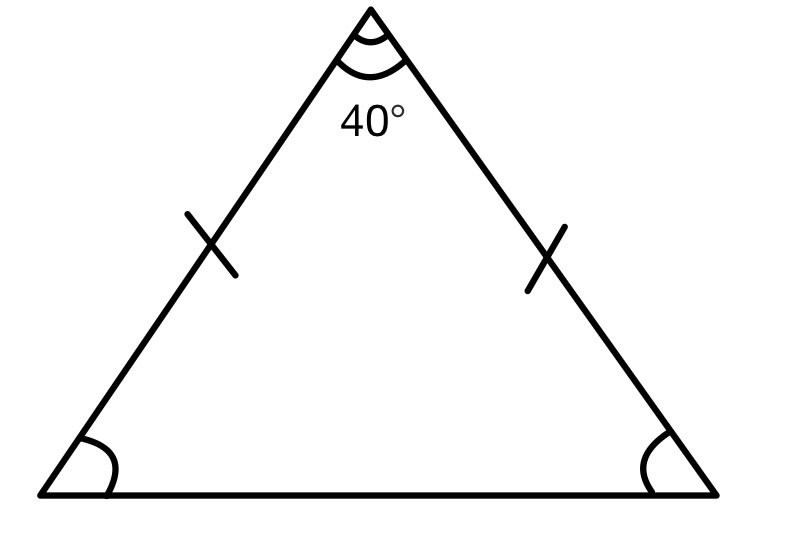
В равнобедренном треугольнике угол при вершине равен Чему равны углы при основании?
Источники:
Сумма углов в треугольнике = Также, в равнобедренном треугольнике углы при основании равны, то есть:
Ошибка.
Попробуйте повторить позже
Найдите значение неизвестного угла.
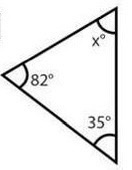
Источники:
Сумма углов в треугольнике = Так как два угла известны, вычислим третий:
Ошибка.
Попробуйте повторить позже
Два угла треугольника относятся как а третий угол равен
Найдите меньший из двух углов.
Источники:
Пусть меньший угол равен градусов, больший угол равен
градусов.
Сумма углов треугольника:
Упрощаем уравнение:
Находим
Меньший угол:
Ошибка.
Попробуйте повторить позже
Найдите значение
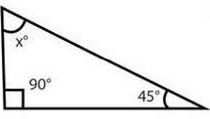
Источники:
Сумма углов в треугольнике = Так как два угла известны, вычислим третий:
С другой стороны, сумма острых углов прямоугольного треугольника – То есть неизвестный угол равен:
Ошибка.
Попробуйте повторить позже
Найдите значение неизвестного угла
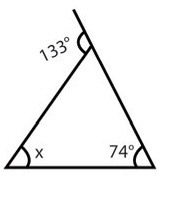
Источники:
Внешний угол треугольника равен сумме двух углов, не смежных с ним, то есть
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике один острый угол в раза больше другого. Найдите меньший угол.
Источники:
Пусть меньший угол равен градусов, тогда больший угол равен
градусов.
Сумма углов треугольника:
Упрощаем уравнение:
Находим угол:
Ошибка.
Попробуйте повторить позже
Сумма углов в треугольнике всегда...
Источники:
Сумма углов в любом треугольнике на евклидовой плоскости равна градусам. Это утверждение является теоремой о сумме углов
треугольника и справедливо для любых треугольников, будь то остроугольные, прямоугольные или тупоугольные.
Ошибка.
Попробуйте повторить позже
Выберите треугольники, существование которых невозможно:
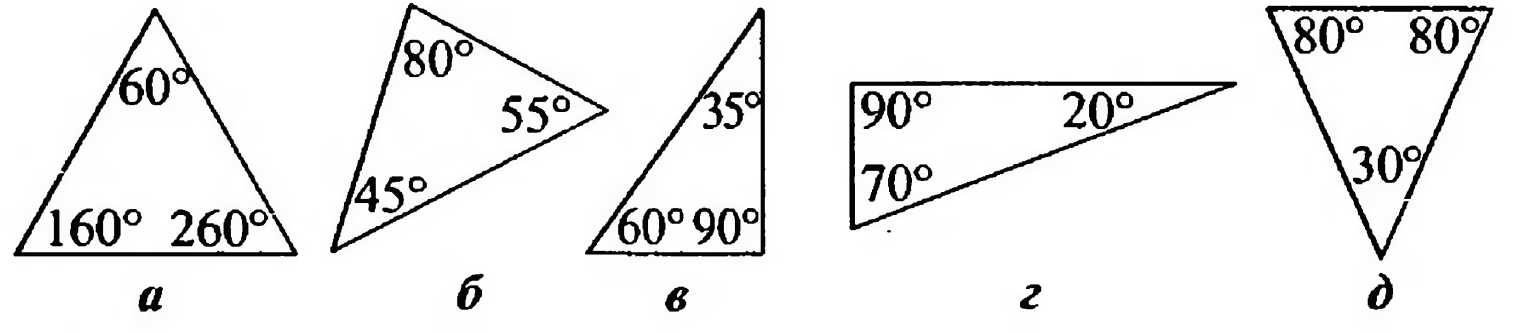
Источники:
Сумма углов треугольника всегда равна
а)
б)
в)
г)
д)
Ошибка.
Попробуйте повторить позже
Какой из перечисленных треугольников существует?
Источники:
Правильный ответ: треугольник, у которого все углы острые (остроугольный треугольник).
- Сумма углов любого треугольника равна
- Два тупых угла (
) уже дают сумму
- Два прямых угла (
) дают
, не оставляя места для третьего угла
- Прямой (
) + тупой (
) дают
Только остроугольный треугольник удовлетворяет условию суммы углов.
Ошибка.
Попробуйте повторить позже
Два угла треугольника равны и
Чему равен третий?
Источники:
Третий угол равен
Ошибка.
Попробуйте повторить позже
В треугольнике угол при вершине равен: а)
б)
в)
Чему равен угол при вершине
если оказывается, что треугольник
равнобедренный и
его основание?
а)
б)
в)
а)
б)
; в)
а)
б)
в)
а)
; б)
; в)
а)
б)
в)
Источники:
Из того, что треугольник равнобедренный и основание получаем
а)
б)
в)
Ошибка.
Попробуйте повторить позже
Найдите ошибку на рисунке. равносторонний.
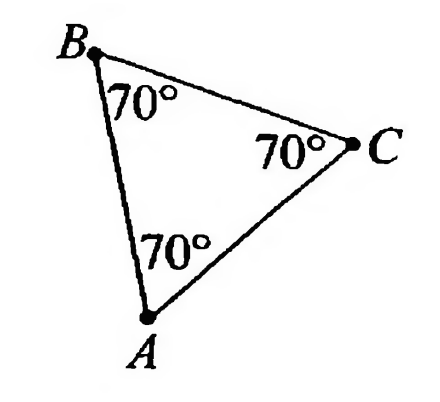
заменить на
заменить на
а остальные оставить как есть
заменить на
а остальные оставить как есть
Источники:
Сумма углов треугольника - Треугольник равносторонний, значит его углы равны:
Ошибка.
Попробуйте повторить позже
равнобедренный, а
равносторонний. Найдите
и
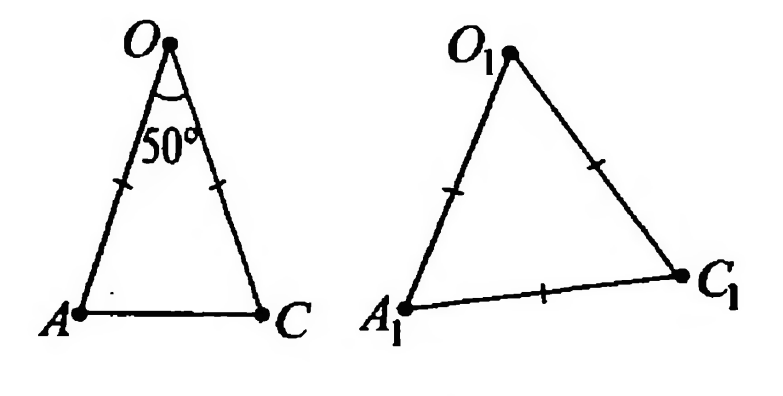
Источники:
Ошибка.
Попробуйте повторить позже
В каком из треугольников больше?
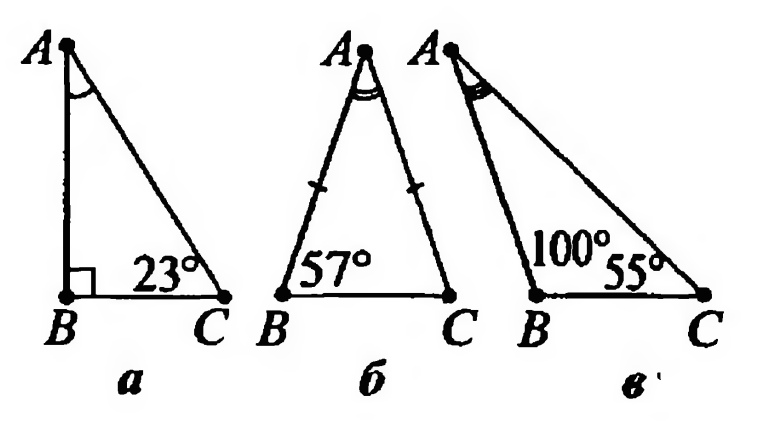
Источники:
а)
б)
в)
Ошибка.
Попробуйте повторить позже
Чему равен угол, который в четыре раза меньше, чем угол равностороннего треугольника?
Источники:
Угол равностороннего треугольника равен . Угол в четыре раза меньше равен
Ошибка.
Попробуйте повторить позже
В каком из треугольников меньше?
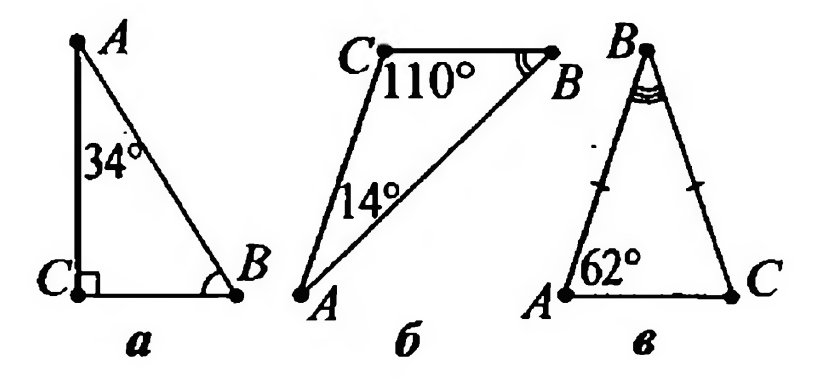
Источники:



